الاحتمالات في لعبة البوكر ذات الخمس بطاقات

مرحباً، أنا مايك، والهدف من هذا الفيديو هو توضيح كيفية حساب الاحتمالات في لعبة بوكر ستاد بخمس بطاقات . بمعنى آخر، ما هو احتمال تكوين أي يد بوكر معينة بخمس بطاقات عشوائية من أصل 52؟ قبل أن أجيب على السؤال المتعلق بعدد مجموعات كل يد بوكر، دعني أطرح عليك سؤالاً أبسط، وإذا كنت تعرف كيفية الحصول على الإجابة، يمكنك الانتقال إلى الجزء التالي.

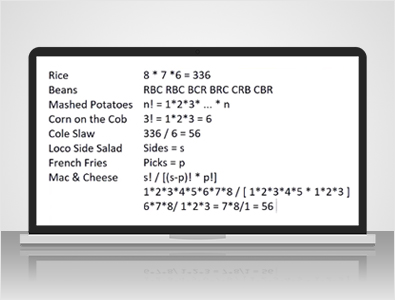
في El Pollo Loco:

لديهم ثمانية أطباق جانبية تُسمى "كلاسيكية"، وقد ذكرتها على اليسار. كما يقدمون بعض الأطباق الجانبية الفاخرة، لكنني لن أُعقّد الأمور بهذا الشأن. إذا طلبت وجبة من ١٢ قطعة، يمكنك اختيار أي ثلاثة من هذه الأطباق الجانبية الثمانية. لنفترض أنه يجب عليك اختيار ثلاثة أطباق مختلفة.

السؤال هو...

...كم عدد الطرق التي يمكنك بها طلب ثلاثة أطباق مختلفة من أصل ثمانية؟ بمعنى آخر، لنفترض أنك تذهب إلى هناك يوميًا، وتطلب ثلاثة أطباق مختلفة. كم يومًا يمكنك أن تقضي دون تكرار الأطباق الثلاثة نفسها؟

إذا كان ترتيب الطلبات مهمًا، فسيكون الجواب ٨ × ٧ × ٦، لأن هناك ثماني طرق لاختيار الأول، وسبع طرق لاختيار الثاني، وست طرق لاختيار الثالث، لكن أمين الصندوق لا يهتم.

إذا قلت -

"أريد أرزًا وفاصوليا وذرة"، ستحصل على نفس النتيجة سواءً قلتَ "أرزًا وفاصوليا وذرة" أو "ذرة وفاصوليا وأرز". كم عدد الطرق المختلفة التي يمكنك بها طلب ثلاثة أطباق جانبية مختلفة؟ حسنًا، لنفترض أنك تحب الأرز والفاصوليا والذرة. يمكنك طلبها بهذا الترتيب: أرز، ذرة، فاصوليا، فاصوليا، أرز. يمكنك طلب فاصوليا، أرز، ذرة، أو ذرة، أرز، فاصوليا، أو ذرة، فاصوليا، أرز، إذن هناك ست طرق ممكنة.

كيف عرفت أنها ستة بدون أن أكتبها فقط؟

حسنًا، هناك صيغة بسيطة جدًا. إذا كان هناك N عنصرًا، فإن عدد طرق ترتيبها هو ١ × ٢ × ٣ مرات حتى نصل إلى N.

في هذه الحالة، كان السؤال: بكم طريقة يمكنك ترتيب ثلاثة أشياء؟ حسنًا، إنها ٣! أي ١ × ٢ × ٣، أي ٦. من بين ٣٣٦ طريقة يمكنك من خلالها ترتيب العناصر الثلاثة من أصل ثمانية، تقسم على ستة لأن هناك ست طرق لترتيب كل مجموعة، فيتبقى لديك ٥٦ طريقة.

ما هي الصيغة العامة، قد تسأل؟

إذا كان هناك، فلنفترض أن عدد الأضلاع يساوي S، وعدد الالتقاطات المسموح لك هو P، فإن الصيغة العامة لعدد طرق التقاط P من S هي s! / s - p! xp!. دعني أوضح أن هذا ينطبق على مثال السؤال.

في هذه الحالة:

س = ٨، إذًا ٨! يساوي ١ × ٢ × ٣ × ٤ × ٥ × ٦ × ٧ × ٨، والمقام لدينا س - ق، أو ٨ - ٣، وهو ما يساوي ٥ أو ٥!. إذن، ١ × ٢ × ٣ × ٤ × ٥، بالإضافة إلى ق! أو ٣!، وهو ما يساوي ١ × ٢ × ٣. يمكنك أن ترى ١ × ٢ × ٣ × ٤ × ٥، وهو ما يساوي ١٢٠، وكلا البسط والمقام، فلنحذف ذلك، ويتبقى لدينا ٦ × ٧ × ٨ / ١ × ٢ × ٣. حسنًا، ٢ × ٣ = ٦، ويظهر الرقم ستة في كل من البسط والمقام، فلنقسمه.

لم يبق لنا سوى...

...٧ × ٨ / ١، أي ٥٦. لأغراض هذا الفيديو، دعوني أقدم دالة. سنسميها C لـ x وy، أي عدد طرق اختيار y عنصر من x، أو x يختار y، كما نقول رياضيًا، وسنعرف ذلك بـ x! / x - y! مضروبًا في y!.

في حالة مثال El Pollo Loco، إذا كان السؤال هو:

"كم عدد الطرق التي يمكنك من خلالها اختيار ثلاث شرائح من أصل ثمانية؟"

سنعبر عن ذلك بهذه الطريقة، وهو ما يساوي - التبديل يساوي ٥٦. أعتقد أننا جاهزون أخيرًا للحديث عن البوكر. ما عدد الطرق التي يمكنك من خلالها اختيار خمس بطاقات من أصل ٥٢؟ حسنًا، هذا يعني ٥٢ اختيار ٥، أي ٥٢! / ٤٧!، ٤٧ لأن ٥٢ - ٥ × ٥!، وهذا يساوي ٢,٥٩٨,٩٦٠. لنبدأ بالفلاش الملكي.

حسنًا، هذا سهل جدًا. هناك أربع مجموعات للفلاش الملكي: القلوب، البستوني، النوادي، والماس.يجب أن تكون الرتب عشرة: ولد، ملكة، ملك، آص. نعم، هناك أربع طرق فقط: ملك وقلوب، ألماس، هراوات، أو بستوني.

ماذا عن الفلاش المستقيم؟

حسنًا، مرة أخرى، لا يزال لدينا الأربعة أنواع، لكن نطاق الفلاش المستقيم يمكن أن يبدأ من الآس، أي الآس، اثنين، ثلاثة، أربعة، خمسة، أو ما يُعرف أيضًا باسم الفلاش المستقيم للعجلة، وصولًا إلى تسعة، عشرة، جاك، ملكة، ملك. إذا كان عشرة، جاك، ملكة، ملك، آس، فسيكون الفلاش الملكي. يمكن أن تتراوح أدنى بطاقة بين الآس والتسعة.

في هذه الحالة...

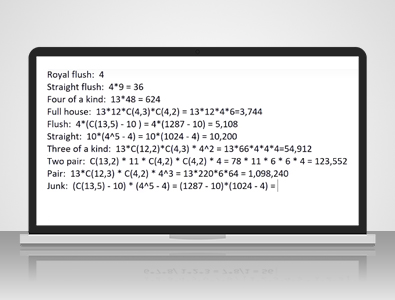
...يُحتسب الآس كالواحد. هناك تسعة احتمالات للفلاش المتتالي، لذا 4 مجموعات × 9 احتمالات = 36. في حالة الأربعة المتشابهة، هناك 13 رتبة محتملة للأربعة المتشابهة، مثلاً، الملكة، ثم يتبقى 48 ورقة في المجموعة للورقة المفردة بعد سحب الأوراق الأربعة للأربعة المتشابهة. هذا يساوي 624.

للمنزل الكامل

هناك ١٣ رتبة ممكنة للثلاثية المتشابهة، و١٢ رتبة متبقية للزوج. للثلاثية المتشابهة، هناك أربع طرق للاختيار، أي ثلاث طرق لاختيار ثلاث مجموعات من أصل أربعة، مضروبة في أربع مجموعات للاختيار، وطريقتان لاختيار مجموعتين من أصل أربعة، للزوج. هذا يساوي ١٣ × ١٢ × ٤ × ٦، أي ٣٧٤٤. أما بالنسبة للفلاش، فلدينا أربع مجموعات للفلاش.

كم عدد الطرق لاختيار خمس رتب من بين 13 رتبة في البدلة المعطاة؟

حسنًا، هذا يعني 13 اختيار 5، ولكن 10 من هذه الطرق ستؤدي إلى ستريت فلش أو رويال فلش. على سبيل المثال، 5، 6، 7، 8، 9 ستؤدي إلى ستريت فلش، لذا علينا اختيار مجموعات الرتب العشر المتتالية. هذا يتبقى لدينا 13 اختيار 5 يساوي 1287، نطرح 10 ونضرب في 4، فنحصل على 5108.

ماذا عن مستقيم؟

حسنًا، كما رأينا للتو في حالة الفلاش، هناك ١٠ نطاقات ممكنة للستريت، بدءًا من الآس، اثنين، ثلاثة، أربعة، خمسة، وصولًا إلى ١٠، ولد، ملكة، ملك، آس. لكل بطاقة، ولكل رتبة في هذا الستريت، هناك أربع مجموعات ممكنة. ٤ × ٤ × ٤ × ٤ × ٤ = ٤^٥، وهو عدد طرق اختيار مجموعة مختلفة لكل بطاقة من البطاقات الخمس. إذا اخترنا المجموعة نفسها في جميع المرات الخمس، فسيتبقى لدينا أيضًا ستريت فلاش أو رويال فلاش. علينا طرح هذه الاحتمالات. ٤^٥ = ١٠٢٤ - ٤ = ١٠٢٠٠ طريقة لتكوين ستريت.

ماذا عن ثلاثة من نفس النوع؟

حسنًا، هناك ١٣ طريقة لاختيار رتبة البطاقات الثلاث المتشابهة، ثم عليك اختيار رتبتين من الـ ١٢ المتبقية للبطاقات الفردية. بعد ذلك، عليك اختيار أربع بطاقات من ثلاث بطاقات للبطاقات الثلاث المتشابهة، ثم بطاقة واحدة من أربع بطاقات لكل بطاقة من البطاقات الفردية.

لدينا ١٣ طريقة لاختيار رتبة البطاقات الثلاث المتشابهة. هناك ٦٦ طريقة لاختيار رتبتين من أصل ١٢ متبقية للبطاقات الفردية، مضروبة في أربع طرق لاختيار ثلاث بطاقات من أصل أربع بطاقات للبطاقات الثلاث المتشابهة، وأربع طرق لاختيار بطاقة واحدة للبطاقات الفردية. الإجابة هي ٥٤٩١٢.

ماذا عن زوجين؟

حسنًا، لديك ١٣ طريقة لاختيار رتبتين من أصل ١٣ لزوجك، ثم ستتبقى رتبة واحدة للفرد. لكل زوج، هناك أربع طرق لاختيار رتبتين من أصل أربعة لزوجك. لديك أربع رتب للفرد. ١٣ طريقة لاختيار رتبتين تساوي ٧٨ × ٦ × ٦ × ٤ = - لقد نسيتُ ١١ رتبة للفرد. ٧٨ × ١١ × ٦ × ٦ × ٤ = ١٢٣٥٥٢.

للزوج

هناك ١٣ طريقة لاختيار رتبة الزوج، ثم عليك اختيار ثلاث رتب من بين الاثنتي عشرة المتبقية للبطاقات الفردية الثلاثة. بالنسبة لزوجك، هناك أربع طرق لاختيار مجموعتين من أربع بطاقات، ثم لكل بطاقة فردية ثلاث بطاقات، هناك أربع مجموعات ممكنة للاختيار من بينها. ٤ × ٤ × ٤ هو عدد الطرق التي يمكنك من خلالها اختيار ثلاث مجموعات للبطاقات الفردية الثلاث، أي ١٣ × ١٢ - ١٢ اختيار ثلاثة يساوي ٢٢٠ × ٦ × ٤^٣ = ٦٤ = ١٠٩٨٢٤٠.

أخيراً

لنحسب احتمال وجود الآس أعلى يسارًا أو أقل، وهو ما سأسميه "غير مرغوب فيه". للحصول على غير مرغوب فيه، يجب أن يكون لديك خمس رتب مختلفة من أصل 13. هناك 13 خيارًا لاختيار خمس رتب من أصل عشرة، ولكن كما رأينا في حالة الفلاش، علينا تحديد مسار الامتدادات العشرية التي تُشكل خطًا مستقيمًا. بعد اختيار الرتب الخمس غير المتتالية، سيكون لديك أربع مجموعات ممكنة لكل رتبة.

تأخذ أربعة إلى القوة الخامسة...

...وكما رأينا مع المتتاليات، علينا أن نطرح أربعة من عدد الطرق لاختيار نفس النوع في كل مرة مما يؤدي إلى الفلاش. 13 اختر خمسة يساوي 1287 ناقص 10 للمتتاليات، ضرب أربعة للقوة الخامسة يساوي 1024 ناقص أربعة يساوي 1302540.

التالي

لنضع كل ذلك في جدول بيانات. دعوني أوضح لكم سريعًا كيفية القيام بذلك في برنامج إكسل. سبق أن رأينا أن هناك أربع طرق فقط للحصول على رويال فلش، واحدة لكل نوع، أي 36 فلاشًا متتاليًا، أي أربعة أنواع مضروبة في تسعة نطاقات ممكنة. للحصول على أربعة من نفس النوع، هناك 13 مرتبة للاختيار من بينها، أربعة من نفس النوع و48 ورقة متبقية للفرد. أما بالنسبة للفول هاوس، فهناك 13 مرتبة للثلاثة من نفس النوع، و12 مرتبة للزوج.

أربعة يختارون ثلاث طرق لاختيار ثلاثة أنواع من نفس النوع. أربعة يختارون طريقتين لاختيار نوعين من أربعة أنواع للزوج. طريقة التعبير عن هذه الصيغة في إكسل هي هذه الصيغة الشائعة التي تجمع بين رقم كبير وفاصلة ورقم صغير، تمامًا كما كتبتها. هذا يعطينا العدد 3744 الذي حصلنا عليه سابقًا.

للتنظيف

هناك أربعة أنواع للاختيار من بينها، 13 بطاقة تختار خمس طرق للاختيار، خمسة منها من أصل 13 في تلك المجموعة، ناقص 10 مجموعات، والتي ستؤدي إلى فلاش متتالي أو فلاش ملكي لأنها متتالية. هذا يبقي لدينا 5108 مجموعات. بالنسبة للمجموعات المتتالية، هناك 10 مجموعات محتملة، أربعة أنواع لكل بطاقة في المجموعة، ولكن بطرح أربعة أنواع للمجموعات الأربعة، نحصل على فلاش متتالي أو فلاش ملكي، ونحصل على 10200.

للثلاثة من نفس النوع

هناك ١٣ رتبة، للثلاثة من نفس النوع، ١٢ يختارون رتبتين للفردين. أربعة يختارون ثلاث طرق لاختيار ثلاث مجموعات من أربع، وأربعة أضعاف أربع طرق لاختيار مجموعتين للفردين. ٥٥٤،٩١٢، ثلاثة من نفس النوع. للزوجين، هناك ١٣ يختارون طريقتين لاختيار مجموعتين من ١٣ للزوجين. يتبقى ١١ للفرد، أربعة يختارون طريقتين لاختيار مجموعتين من أربع للزوجين وأربع مجموعات للفرد.

بالنسبة للزوج، لدينا ١٣ رتبة للزوج، يختار ١٢ منهم ثلاث طرق لاختيار ثلاث رتب من أصل ١٢ لثلاثة سينجلتون. يختار أربعة منهم طريقتين لاختيار بدلتين من أصل أربعة للزوج، ويختار أربعة أس ٣ طرقًا لاختيار ثلاث بدلات لثلاث سينجلتون.

وأخيرا، بالنسبة للخردة

هناك ١٣ طريقة لاختيار خمس رتب من أصل ١٣، مطروحًا منها ١٠ طرق متتالية تُعطيك سلسلة أوراق، وأربع طرق لاختيار كل نوع. أربعة أس ٥ مطروحًا منها أربعة للطرق التي تُعطيك سلسلة أوراق. كما ترى، مجموع هذه الطرق هو ٢٬٥٩٨٬٩٦٠، وهو ما ذكرناه أيضًا في بداية هذا الفيديو. حسنًا، لننتقل إلى تطبيق عملي لكل هذا.

واحدة من مئات ألعاب الكازينو التي أقوم بتغطيتها على موقعي Wizard of Odds هنا تسمى : Let it ride .

دعونا نفتح هذه الصفحة وهذه لعبة بوكر تعتمد على يد بوكر مكونة من خمس بطاقات، لا يوجد سحب، بل يعتمد كل شيء على خمس بطاقات عشوائية فقط من أصل 52. لن أتطرق إلى قواعد اللعبة بالكامل ولكن هناك رهان جانبي يدفع بناءً على قيمة البوكر الخاصة ببطاقاتك الخمس فقط.

يمكنك أن ترى...

أدرجتُ هنا تسعةً من جداول الدفع المحتملة، لكن الجدول الرابع هنا شائعٌ جدًا. لقد نقلتُه إلى هذا الجدول، تكلفة الرهان دولار واحد. إذا حصلتَ على رويال فلاش، فستربح 20,000 دولار، وإذا حصلتَ على ستريت فلاش، فستربح 20,000 دولار، وإذا حصلتَ على أربعة من نفس النوع، فستربح 400 دولار. بالمناسبة، هذه الرهانات تُدفع على أساس 4-1، مما يعني أنك لا تحتفظ برهانك الأصلي إذا فزتَ.

إليك جميع التركيبات التي عملت بالفعل على حساب احتمالاتها، وهذا العمود العائد هنا هو حاصل ضرب الفوز في الاحتمالية.

على سبيل المثال، هناك:

كما نعلم سابقًا، احتمال الحصول على رويال فلاش يبلغ حوالي أربعة ملايين واثنين ونصف مليون. إذا ضربنا هذا الاحتمال في ٢٠٠٠٠، فسيكون العائد المتوقع ٣.٠٨ سنتًا. هذا هو المبلغ الذي يتوقع اللاعب الحصول عليه من أرباح رويال فلاش إذا راهن بدولار واحد. ويمكنه أن يتوقع الحصول على ٢.٧٧ سنتًا لمجموعات ستريت فلاش، وهكذا.

إذا أجرينا جميع الحسابات، فسنجد أن اللاعب الذي راهن بدولار واحد سيحصل على 74.4667 سنتًا. بمعنى آخر، مقابل هذا الدولار، سيحصل اللاعب على حوالي 74 سنتًا.47% وسيحتفظ الكازينو بـ 25.53%.

الطريقة التي أود أن أعبر بها عن ذلك...

... ميزة الكازينو هي ٢٥.٥٣٪، لذا دع الأمر يستوعبه قليلًا. يحتفظ الكازينو بأكثر من ٢٥٪ من هذا الرهان، وهذا يُظهر ما كنت أقوله لأكثر من ٢٠ عامًا، وهو أن الرهانات الجانبية جميعها رهانات خاسرة. إذا استفدت شيئًا واحدًا فقط من هذا الفيديو، فأرجو أن يكون هو. هذا الفيديو طويل بما فيه الكفاية، وأعتذر عن طوله، وآمل أن يكون مفيدًا وأنك استفدت منه.

شكرا لمشاهدتك.

كتبه: Michael Shackleford