فيديو عن احتمال القوس المثالي

مرحبًا، أنا مايك، وهذا الفيديو سيحاول الإجابة على السؤال: ما هو احتمال ملء قوس March Madness المثالي؟

سأفترض أن لديك بالفعل بعض المعرفة الأساسية حول كيفية عملها ، ولكن باختصار شديد، هناك 64 فريق كرة سلة يتنافسون في بطولة إقصائية واحدة؛ وهذا يعني أنه سيكون هناك 63 مباراة إجمالية.

يُقسّمون البطولة إلى أربعة أقسام ، وفي كل قسم، في الجولة الأولى، يلعب الفريق المصنف أولًا مع الفريق المصنف سادس عشر، ويلعب المصنف ثانيًا مع الخامس عشر، ويلعب الثالث مع الرابع عشر، وهكذا. ثم يُختار الفائزون من جميع مباريات الجولة الأولى، ثم يتواجهون في الجولة الثانية، وفي النهاية، ينتهي الأمر بفائز واحد فقط.

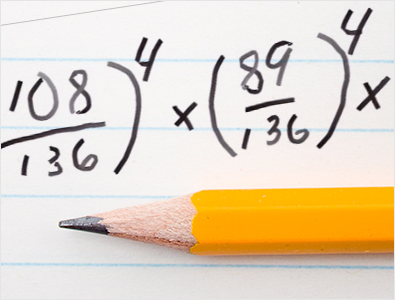
الآن كل شهر مارس...

...يُطرح هذا السؤال دائمًا في وسائل الإعلام، ما هو احتمال اختيار الفائز المثالي؟ يُقشعرّ شعر رقبتي عندما أسمع الرقم 1 من 9 كوينتيليون، 223 كوادريليون، 372 تريليون، 36 مليار، 854 مليون، 781,000؛ أعتقد ذلك. هذا ببساطة هو احتمال التنبؤ الصحيح بـ 63 رمية عملة متتالية. لا أعتقد أن أحدًا يُحدد الفائز في بطولة مارس مادنس بهذه الطريقة، لأن بعض الفرق أفضل من غيرها بوضوح. على سبيل المثال، الفريق المصنف الأول أفضل من الفريق المصنف السادس عشر.

قبل أن أذهب إلى أبعد من ذلك...

دعوني أقول إن هذا الفيديو صُوّر في أبريل ٢٠١٨، لذا فهو مبني على جميع مباريات بطولة مارس مادنس التي لُعبت من عام ١٩٨٥ إلى عام ٢٠١٨. حسنًا، أردتُ أيضًا التطرق إلى فيديو آخر على يوتيوب للأستاذ جيف بيرغن . يقول إنه باتباع استراتيجية لا يتطرق إليها، فإن احتمالية ظهور قوس مثالي هي ١ من ١٢٨ مليار. هذا الرقم قريب جدًا من الرقم الذي حصلتُ عليه.

أود أن أتحدى البروفيسور بيرغن أن يشرح بالتفصيل كيفية حصوله على هذا الرقم، لكنني سأشرح لكم كيف حصلت على رقمي. استراتيجيتي بسيطة للغاية. تختار دائمًا الفريق الأعلى تصنيفًا في كل مباراة، وفي النهاية، سيتبقى لديك أربعة فرق فقط مصنفة في المركز الأول، وفي هذه الحالة يمكنك الاختيار عشوائيًا.

قبل أن يكتب أحد على التعليقات

دعني أقول لك أنه يمكنك تحسين هذا الأمر بشكل أكبر من خلال النظر إلى الاحتمالات الحالية للألعاب، وعلى سبيل المثال، عندما يتعلق الأمر ببذرة واحدة ضد بذرة واحدة، يمكنك إلقاء نظرة على احتمالات الذهاب إلى الخارج في لاس فيجاس لمعرفة من لديه فرصة أفضل للفوز، لكنني لن أتطرق إلى ذلك.

سيعتمد هذا الفيديو ببساطة على اختيار الفريق الأفضل تصنيفًا في كل مرة، ومرة أخرى، عندما يتراجع تصنيف الفرق الأربعة الأولى، يتم الاختيار عشوائيًا. حسنًا، هذا كل ما عليّ قوله في المقدمة.

اسمحوا لي أن أعتذر مقدمًا عن استخدامي لجهاز لوحي في الجزء التالي من هذا الفيديو. واجهتُ بالفعل العديد من المشاكل التقنية في تشغيله بشكل صحيح، لذا قررتُ تصوير المقدمة بهذه الطريقة. دون مزيد من اللغط، إليكم كيفية حساب احتمالية الفوز المثالي في بطولة March Madness باتباع الاستراتيجية التي ذكرتها للتو.

حسنًا، هنا نذهب:

هذا أول فيديو لي أُنتجه باستخدام لوح رسم إبداعي، إن صح التعبير. لطالما رغبتُ في إنتاج فيديوهات مشابهة لأكاديمية خان، ولكن عن المقامرة والرياضيات. بعد هذه المقدمة، لننتقل مباشرةً إلى الحسابات.

أُقدّر احتمال فوز المصنف الأول على المصنف السادس عشر بـ ١٣٥ من ١٣٦، لأنه حتى الآن، أُقيمت ١٣٦ مباراة من هذا النوع، وفاز المصنف الأول ١٣٥ مرة. هذا يعني أن احتمال فوز المصنف الأول في أي مباراة هو ٩٩.٢٦٪.

لكن...

... هناك أربعة أقسام مختلفة، لذا عليك تحقيق ذلك أربع مرات مختلفة، لذا خذ هذا إلى القوة الرابعة.

هناك أيضًا أربع مباريات مختلفة يلعب فيها المصنف الثاني ضد المصنف الخامس عشر. حدث هذا في 136 مرة. فاز المصنف الثاني 127 مرة. بناءً على البيانات التاريخية، فإن احتمال فوز المصنف الثاني على المصنف الخامس عشر هو 93.38%، ويجب تكرار ذلك أربع مرات أيضًا في الأقسام الأربعة المختلفة.

وبالمثل، فإن احتمال فوز المصنف الثالث على المصنف الرابع عشر هو ١١٥ مقسومًا على ١٣٦، ويجب تكرار ذلك أربع مرات. ثم يكون احتمال فوز المصنف الرابع على المصنف الثالث عشر هو ١٠٨ مقسومًا على ١٣٦، ويجب تكرار ذلك للقوة الرابعة في المباريات الأربع التي يتعين عليك الفوز بها.

احتمال فوز المصنف الخامس على المصنف الثاني عشر هو 89 في 136، أي حوالي 65.44%، مرفوعًا للقوة الرابعة. احتمال فوز المصنف السادس على المصنف الحادي عشر هو 85 في 136، أي 62.5% في أي مباراة. احتمال فوز المصنف السابع على المصنف العاشر هو 83 في 136. احتمال الفوز في كل مباراة هو 61.03%. وأخيرًا، احتمال فوز المصنف الثامن على المصنف التاسع هو 71 في 136، ويجب تكرار ذلك أربع مرات.

إذا فزت بكل هذه المباريات...

ستتجاوز الجولة الأولى. ثم في الجولة الثانية، سيواجه المصنف الأول المصنفين الثمانية. حدث هذا 72 مرة حتى الآن، ومن بين هذه المرات، تغلب المصنف الأول على المصنف الثامن 58 مرة. احتمال فوز المصنف الأول على المصنف الثامن هو 80.56%، ويتبقى عليك تكرار ذلك أربع مرات.

بعد ذلك، سيلعب المصنفون الأربعة ضد المصنفين الخمسة. حدث هذا 73 مرة حتى الآن، وفاز المصنف الرابع 41 مرة باحتمالية 56.16% في كل مباراة، وما زال لدينا أربع مجموعات، لذا ارفع النتيجة إلى القوة الرابعة.

بعد ذلك، سيلعب المصنفون الثلاثة ضد المصنفين الستة. فاز المصنفون الثلاثة 41 مرة من أصل 70 مرة، بنسبة احتمال فوز 58.57% في كل مباراة. وأخيرًا، لتجاوز الجولة الثانية، سيلعب المصنفان الثانيان ضد المصنفين السبعة. فاز المصنف الثاني 56 مرة، وحدث ذلك 79 مرة، بنسبة احتمال 70.89% في كل مرة. حسنًا، بافتراض فوزك بجميع هذه المباريات، ستنتقل إلى الجولة الثالثة حيث سيلعب المصنف الأول ضد المصنفين الأربعة.

حدث هذا 61 مرة حتى الآن في تاريخ البطولات ، وفاز المصنف الأول 44 مرة، بنسبة احتمال 72.13% في كل مرة. بعد ذلك، سيلعب المصنفان الثاني والثالث ضد المصنفين الثالث. حدث ذلك 52 مرة حتى الآن، وفاز المصنف الثاني 32 مرة منها. مرة أخرى، لا يزال يتعين تكرار ذلك أربع مرات مختلفة.

على افتراض أنك فزت بكل تلك الألعاب:

عندها، سيتبقى لديك فقط تصنيف واحد وتصنيفان. احتمال فوز تصنيف واحد على تصنيف اثنين هو ٣٥ في ٦٤ مباراة، بناءً على المباريات السابقة، وهذا لا يزال يجب أن يتكرر أربع مرات في الأقسام الأربعة.

الآن، إذا وصلت إلى هذه المرحلة... ستكون قد فزت بجميع الأقسام الأربعة ، وسيكون الفريق الأول متصدرًا في كل مرة. هنا تبدأ عملية الاختيار العشوائي. ستحتاج إلى ثلاث مباريات أخرى لتحديد الأفضل من بين الفرق الأربعة، وكما ذكرتُ في المقدمة، تختار عشوائيًا، لذا ستكون فرص فوزك في كل مرة 1 من 2، بالإضافة إلى ثلاث مباريات أخرى.

هذا هو احتمال فوزك باستخدام استراتيجيتي ، وهو ١ من ٤٢,٧٤٣,٨٩٠,٥٥٢. هذا كل ما في الأمر. أعتقد أن هذا هو الرقم الأكثر دقة لاختيار أفضل لاعب في بطولة مارس مادنس.

كما ذكرتُ في المقدمة، يُمكنك تحسين هذا الأمر بالاطلاع على الاحتمالات الحالية في سوق المراهنات، وشكرًا لك على مشاهدة هذا الفيديو. أعلم أنه لم يكن جيدًا.

اعتبر هذا تجربة تعلّم لي، وكل هذا مُدوّن على موقعي الإلكتروني wizardofodds.com في قسم المراهنات الرياضية، ثم ابحث عن صفحة كيفية ملء نموذج مثالي لبطولة March Madness. لا أعتقد أن هناك المزيد لأقوله.

شكرا لك على المشاهدة.

كتبه: Michael Shackleford