سيك بو - احسب الاحتمالات واربح | فيديو

مرحبًا بالجميع، هذا مايك.

ستتعلم كيفية حساب احتمالات الفوز في لعبة سيك بو . باختصار، سيك بو لعبة صينية قديمة جدًا تعتمد على رمي ثلاثة نرد. هناك مجموعة واسعة من الرهانات للاختيار من بينها في اللعبة.

ماذا سأفعل :

سأقسم هذا الموضوع إلى مقطعي فيديو لأن الجميع في منتداي يشتكون من طول مقاطع الفيديو. في هذا الجزء الأول ، سأشرح كيفية حساب احتمالية الحصول على مجموع من 3 إلى 18 بثلاثة أحجار نرد، بالإضافة إلى احتمالية الحصول على 0 أو 1 أو 2 أو 3 من أي وجه نرد.

بمجرد أن نكون مسلحين بالإجابات على تلك الأسئلة...

...يمكننا الانتقال إلى الجزء الثاني وتحليل نوع القيمة التي تحصل عليها مع كل الرهانات المختلفة في لعبة Sic Bo.

لنُجب على السؤال : "ما هو احتمال الحصول على مجموع مُحدد بثلاثة أحجار نرد سداسية الأوجه؟" هذه التقنية التي سأعرضها لكم ستنطبق على أي عدد من أحجار النرد.

أود أن أشيد بهذه التقنية البسيطة والدقيقة لروبرت جودهاند من سومرست، المملكة المتحدة. تناولتها في عمود "اسأل الساحر" رقم ٢٦٤. سأشاركها معكم الآن.

أولًا، ما علينا فعله هو تحديد خمسة مربعات وهمية. ستفهمون السبب بعد قليل. الآن، سأسرد جميع الأرقام من ١ إلى ١٨. باستخدام حجر نرد واحد، من البديهي أن هناك طريقة واحدة للحصول على ١ أو ٢ أو ٦.

لكل وجه جانب، لذا فالأمر واضح جدًا. باستخدام نردين، ما عليك فعله هو جمع العمود الأيسر، وهو العمود B في هذه الحالة، بدءًا بخلية واحدة متجهًا إلى الطرف الأيسر، ثم الخلايا الخمس التي تعلوها.

في الحالة الراهنة…

أعمل على الخلية C8. هذا يمثل عدد طرق رمي نردين للحصول على مجموع اثنين. أحسب مجموع القيم في الخلايا B2 إلى B7. إذا كانت الخلية فارغة، فسيفترض Excel أنها صفر.

سأنسخ وألصق هذا مع جميع الاحتمالات حتى ١٢. ستلاحظ أنه لمجموع اثنين، هناك طريقة واحدة لرمي الكرة. لمجموع ثلاثة، هناك طريقتان. لمجموع أربعة، هناك ثلاث طرق.

حسنًا، لماذا يعمل هذا؟

لنفترض أن مجموع الاثنين هو اثنان. للحصول على مجموع اثنين، يجب أن يكون النرد الأول واحدًا، ثم يكون النرد الثاني واحدًا. هناك طريقة واحدة فقط ليكون النرد الأول واحدًا، وبالطبع طريقة واحدة فقط ليكون النرد الثاني واحدًا. للحصول على مجموع ثلاثة، هناك طريقتان.

هناك طريقة واحدة يمكن أن يكون فيها النرد الأول واحدًا والثاني اثنين ، بالإضافة إلى طريقة واحدة يمكن أن يكون فيها النرد الأول اثنين والثاني واحدًا. للحصول على أربعة، يجب أن يكون النرد الأول واحدًا إلى ثلاثة.

بمجموع خمسة...

يجب أن يكون مجموع النرد الأول من واحد إلى أربعة. طالما كان النرد الأول ضمن هذا النطاق المقبول، فهناك طريقة واحدة يمكن أن يصل بها النرد التالي إلى المجموع الذي تتحدث عنه.

دعنا ننتقل إلى النرد الثلاثة

إنها نفس التقنية تمامًا. يمكننا ببساطة نسخ ولصق الصيغة نفسها. يمكنني أخذ هذا من أي مكان في النطاق الذي حددناه للتو. سأفعل هنا، أنسخه وألصقه في خلية واحدة إلى اليمين، ثم أنسخه وألصقه لأسفل. لدينا هنا عدد التركيبات لأي مجموع من 3 إلى 18 باستخدام ثلاثة أحجار نرد.

على سبيل المثال:

هناك طريقة واحدة للحصول على مجموع ثلاثة، وثلاث طرق للحصول على مجموع أربعة، وست طرق للحصول على مجموع خمسة، وهكذا. لماذا ينجح هذا؟ قد تسأل مجددًا. حسنًا، لننظر إلى مجموع سبعة، على سبيل المثال. للحصول على مجموع سبعة بثلاثة نرد، يمكن ذلك إذا كان المجموع باستخدام نردين هو اثنين، ثم أضفنا إليه خمسة.

هناك طريقة واحدة يمكن أن يكون فيها أول نردين مجموعهما اثنين. وهناك طريقة أخرى وهي أن يكون مجموع أول نردين ثلاثة، ثم يكون مجموع النرد الثالث أربعة. كما رأينا، هناك طريقتان يمكن أن يكون مجموع أول نردين ثلاثة، وثلاث طرق يمكن أن يكون مجموع أول نردين أربعة.

للحصول على المجموع سبعة …

يجب أن يكون مجموع نرديك الأولين من اثنين إلى ستة. رأينا للتو أن العدد الإجمالي للطرق الممكنة هو مجموع من واحد إلى خمسة، أي 15. لنضع كل هذا في جدول سهل الاستخدام. مرة أخرى، إليك مجموعك.

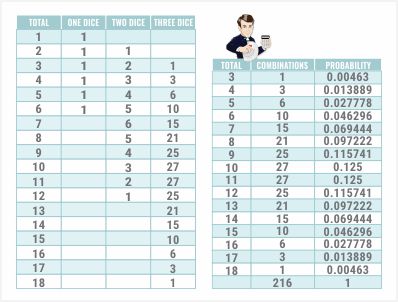
وهنا التركيبات :

لنأخذ المجموع ٢١٦. يبدو هذا الرقم مألوفًا. ربما يكون ستة أس ثلاثة.

وأخيرًا، دعونا نجد احتمال كل إجمالي:

نأخذ عدد التركيبات مقسومًا على الإجمالي. هناك احتمال الحصول على مجموع من 30 إلى 18. لننظر الآن إلى احتمال رمي أي وجه نرد من صفر إلى ثلاث مرات. هناك ستة رهانات مختلفة في لعبة سيك بو، رهان واحد لكل وجه نرد.

يفوز اللاعب بنسبة واحد لواحد إذا رُمي الوجه المختار مرة واحدة، واثنين لواحد إذا رُمي مرتين، وثلاثة لواحد إذا رُمي ثلاث مرات. يُخطئ الكثيرون في إضافة الاحتمالات عند الحديث عن أحداث متعددة، فكل نرد يُمثل حدثًا مستقلًا.

نحن لا نجمع، بل نضاعف.

أحب التفكير في الأشياء في مجموعات أولًا. لنفترض أنك اخترت الرقم ستة، على سبيل المثال. ما هو - أو بالأحرى - عدد مجموعات الطريقة التي يمكن أن يظهر بها الرقم ستة ثلاث مرات على ثلاثة نرد؟ حسنًا، إنه ببساطة واحد. هناك طريقة واحدة فقط يمكن أن يحدث بها ذلك، 6-6-6. ماذا عن مرتين؟

على سبيل المثال:

٦-٦-٤ أو ٢-٦-٦، ٦-١-٦. اثنان من النرد يحملان الرقم ستة، وواحد منهما يحمل رقمًا آخر. يمكن أن يكون الرقم الآخر أيًا من الوجوه الخمسة الأخرى، ويمكن أن يظهر هذا الرقم على أي من النردات الثلاثة. إجمالي عدد مرات ظهور وجه النرد الذي اخترته مرتين من أصل ثلاثة نرد هو ١٥ مرة.

ماذا عن عدد الطرق التي يمكن أن تظهر بها مرة واحدة؟

حسنًا، النردان الآخران اللذان لم تختارهما يمكن أن يكونا أيًا من خمسة وجوه. نضرب ٥ × ٥ لأن أحدهما يمكن أن يكون أي شيء آخر غير الرقم ستة أو أيًا كان ما تختاره، والآخر يمكن أن يكون أيًا من الوجوه الخمسة الأخرى.

أخيراً…

...نضرب في ثلاثة لأن حجر النرد الذي اخترته يمكن أن يكون أيًا من النردات الثلاثة. عدد مرات رميك للوجه الذي اخترته في المرة الواحدة هو 5 × 5 × 3، أي 75. على سبيل المثال، لنفترض أنك اخترت الوجه السادس، فقد يكون 6-1-2، 1-4-6، 1-6-5، 2-6-2، 6-1-3، وهكذا.

ماذا عن عدد التركيبات التي لا تؤدي إلى ظهور أي وجه من وجوه النرد التي اخترتها؟

حسنًا، كلٌّ من النرد الثلاثة يمكن أن يكون واحدًا من خمسة أشياء. خمسة نرد - أعني ثلاثة نرد، لكلٍّ منها خمس مجموعات مختلفة، بخلاف الوجه الذي اخترته، يكون المجموع 5 × 5 × 5 مجموعات، أو 125. لنأخذ مجموع هذه المجموعات، فنحصل على 216 مرة أخرى. مرة أخرى، هذا يساوي ستة أس ثلاثة، لذا لا بد أنني فعلتُ شيئًا صحيحًا.

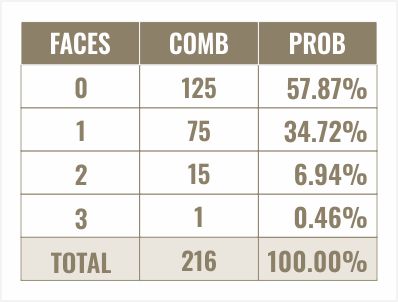
وأخيرا، دعونا ننظر إلى الاحتمالية

ببساطة، نأخذ عدد التركيبات مقسومًا على إجمالي التركيبات. لنضع ذلك في النسبة المئوية. نرى هنا أن احتمال ظهور الوجه الذي اخترته صفرًا هو ٥٧.٨٧٪، ومرة واحدة ٣٤.٧٢٪، ومرتين ٦.٩٤٪، وثلاث مرات ٠.٤٦٪.

آمل أن يكون ذلك واضحًا. إلى اللقاء في الجزء الثاني حيث أحسب احتمالات العديد من رهانات سيك بو المختلفة.

شكرا للمشاهدة.

تم إعداد هذه الوثيقة باستخدام محرر HTML الفوري. انقر هنا وجرّبها مجانًا.

الجزء الثاني

كتبه: Michael Shackleford