اسأل الساحر #171
أنا لا أفهم لعبة نيم الخاصة بك! لطالما اعتقدت أن مفتاح الفوز هو ترك خصمك (في هذه الحالة، الحاسوب) مع نقاط مجموعها يساوي العدد الأدنى التالي الذي يساوي مجموعها بالأرقام الثنائية، أي إذا كان لديّ 17 نقطة، فسأأخذ 2 وأترك 15، أي مجموع الأرقام الثنائية 1، 2، 4، 8. لكن يبدو أن هذا لا ينجح. هل أنا على صواب أم خطأ؟
أنت على الطريق الصحيح مع الأرقام الثنائية، ولكن هذه ليست استراتيجية الفوز تمامًا. أولًا، إذا استطعت ترك خصمك بعدد فردي من الصفوف، كل صف يحتوي على رقم واحد، فافعل ذلك. وإلا، فقسّم كل صف إلى مكوناته الثنائية. على سبيل المثال، 99 يساوي 64 + 32 + 2 + 1. ثم اجمع عدد كل مكون على جميع الصفوف. ثم ابحث عن طريقة تجعل خصمك يمتلك عددًا زوجيًا من جميع المكونات الثنائية على جميع الصفوف.
لنلقِ نظرة على مثال. لنفترض أن دورك في السيناريو التالي.
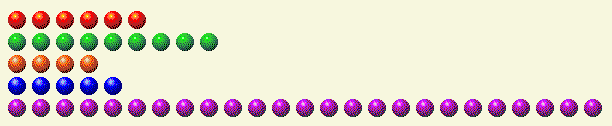
يقوم الجدول التالي بتقسيم كل صف إلى مكوناته الثنائية.
دور اللاعب 1
| صف | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 25 | 1 | 0 | 0 | 1 | 1 |
| المجموع | 3 | 1 | 3 | 2 | 1 |
كما ترى، هناك عدد فردي من الآحاد والاثنينات والأربعات والستة عشر. من الواضح أننا نحتاج إلى وضع صف الـ ٢٥ تحت ١٦ لحذف الوحدة ١٦. وللحفاظ على مجموع العناصر الثنائية زوجيًا، نحتاج إلى حذف ١، وإضافة ٢، وإضافة ٤، والإبقاء على ٨، ثم حذف ١٦. هذا يعني أن أفضل طريقة هي ٢ + ٤ + ٨ = ١٤ في الصف الأخير. وبترك ١٤ في الصف السفلي، نحصل على ما يلي.
دور الكمبيوتر 1
| صف | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 14 | 0 | 1 | 1 | 1 | 0 |
| المجموع | 2 | 2 | 4 | 2 | 0 |
يأتي دور الكمبيوتر، ويترك لنا هذا.
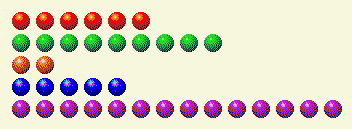
وهنا التقسيم الثنائي لذلك.
دور اللاعب الثاني
| صف | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 14 | 0 | 1 | 1 | 1 | 0 |
| المجموع | 2 | 3 | 3 | 2 | 0 |
هنا نحتاج إلى حذف ٢ و٤ لنحصل على المجموعين متساويين. يوجد صف واحد فقط، وهو الصف ١٤، والذي يحتوي على كلا العنصرين. لذا، نحذف ٦ منه، ليتبقى ٨.
دور الكمبيوتر الثاني
| صف | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 0 |
| المجموع | 2 | 2 | 2 | 2 | 0 |
يأتي دور الكمبيوتر، ويترك لنا هذا.
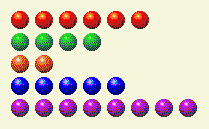
الآن نحتاج إلى تغيير الأعمدة 1 و 4 و 8.
دور اللاعب الثالث
| صف | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 0 |
| المجموع | 1 | 2 | 3 | 1 | 0 |
يمكن القيام بذلك عن طريق تغيير الصف من 8 إلى 5 على النحو التالي.
دور الكمبيوتر الثالث
| صف | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| المجموع | 2 | 2 | 4 | 0 | 0 |
يأتي دور الكمبيوتر، ويترك لنا هذا.
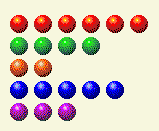
الآن نحتاج إلى تغيير الإجمالي 2 و 4.
دور اللاعب الرابع
| صف | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| المجموع | 2 | 3 | 3 | 0 | 0 |
يمكن القيام بذلك عن طريق تغيير الرقم 6 إلى 0.
دور الكمبيوتر الرابع
| صف | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| المجموع | 2 | 2 | 2 | 0 | 0 |
يأتي دور الكمبيوتر، ويترك لنا هذا.
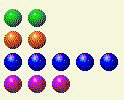
الآن نحتاج إلى تغيير 2 و 4.
دور اللاعب الخامس
| صف | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| المجموع | 2 | 3 | 1 | 0 | 0 |
يمكن تحقيق ذلك عن طريق تغيير الصف من 5 إلى 3. إذا تمكنت يومًا ما من جعل خصمك يصل إلى موقف x،x،y،y، فلن يمكنك إلا الفوز، إذا تمكنت من الحفاظ على نفس الموقف حتى النهاية.
دور الكمبيوتر الخامس
| صف | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| المجموع | 2 | 4 | 0 | 0 | 0 |
في الحركات القليلة التالية، أبقي الحاسوب على أنماط س، س، ص، ص. هنا يتركني الحاسوب مع ٢، ٢، ٣، ٢؛ لذا أتركه مع ٢، ٢، ٢، ٢.

ثم يُعطيني الحاسوب ٢، ٢، ١، ٢. فأتركه مع ٢، ٢، ١، ١.
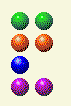
ثم يتركني الحاسوب مع ٢، ٢، ١. فأتركه مع ٢، ٢. إذا استطعتَ يومًا ما أن تجعل خصمك يصل إلى صفين متساويين، فلا مفر من الفوز، فقط حافظ على تساوي الصفين.

ثم يتركني الكمبيوتر مع كومة واحدة من 2، وأقوم بإزالة 1.

وهنا نهاية اللعبة.
أفهم أن رهان "الوضع" رهان جيد عندما تكون احتمالات الفوز 10x أو أكثر. لذا، إذا كانت النتيجة 6 أو 8، راهن بـ 5 دولارات بالإضافة إلى 50 دولارًا من الاحتمالات المجانية على سبيل المثال. سؤالي هو: لماذا الانتظار حتى تظهر النتيجة؟ لماذا لا نراهن على خط المرور، ثم إذا كانت النتيجة 6 أو 8، نراهن بكامل احتمالات الفوز 10x؟ بهذه الطريقة تحصل على أفضلية الاحتمالات، بالإضافة إلى ميزة رمية "الخروج" 7/11. هل أغفل شيئًا؟
أوافقك الرأي. لا أنصح بوضع رهانات "الوضع" أو "الوضع"، لأنه كما ذكرتَ، تكون احتمالات الربح أفضل عند وضع رهان خطي ثم أقصى احتمالات. مع ذلك، يجب على بعض الأشخاص المراهنة على النقاط مباشرةً. إذا كان هذا الأمر مُسلّمًا به، فإنني أنصح بوضع أفضل رهان بين "الوضع" و"الشراء" و"الوضع"، وهو ما سأشرحه بتفصيل أكبر في قسم "الكرابس".
كان صديقي يلعب في لاس فيغاس. دار بيننا جدال حاد حول أيهما أفضل إحصائيًا، هل مضاعفة الرهان بمجموع أوراق اللاعب ١٠ مقابل ٧ أوراق للموزع، أم مضاعفة الرهان بمجموع أوراق اللاعب ١١ مقابل ١٠ أوراق للموزع، في لعبة بمجموعتين من الأوراق. ظننتُ أن السبب هو الخيار الأول.
تم إعداد ملحق البلاك جاك رقم 9 خصيصًا لهذه الأنواع من الأسئلة. بافتراض وجود 6 مجموعات أوراق، يُظهر جدولي أن القيمة المتوقعة لمضاعفة 8 + 2 مقابل 7 هي 0.396342. والقيمة المتوقعة لمضاعفة 8 + 3 مقابل 10 هي 0.176919. إذًا أنت محق، 10 مقابل 7 هي اليد الأفضل بكثير.
موقعك رائع، لقد تعلمت منه الكثير. في لعبة البوكر هولدم، عندما يكون لديك ٢٠ ورقة تُعطيك اليد الرابحة. لماذا تكون نسبة تكوين يدك عند النهر ٦٧.٥٪ وليس ٨٦٪ (٢٠/٤٧ + ٢٠/٤٦)؟ بحثت في كل مكان ولم أستطع فهم هذا، مع أنني أعلم أنه ربما يكون بسيطًا جدًا. سأكون ممتنًا للمساعدة، شكرًا!
شكراً! طريقتك هي مضاعفة احتمال الحصول على بطاقتين من أصل العشرين بطاقة التي تحتاجها. احتمال حصولك على واحدة من العشرين بطاقة المطلوبة في الدور هو ٢٠/٤٧ = ٠٫٤٢٥٥. احتمال عدم حصولك عليها في الدور ثم حصولك عليها في النهر هو (٢٧/٤٧) × (٢٠/٤٦) = ٠٫٢٤٩٨. إذن، الاحتمال الإجمالي هو ٠٫٤٢٥٥ + ٠٫٢٤٩٨ = ٠٫٦٧٥٣.
شهدتُ مؤخرًا موقفًا في كازينو قبلي محلي يتعلق بالبروتوكول على طاولة الكرابس، حيرني، وأتساءل إن كنتَ قد أوضحتَه لي. في رمية الخروج، رمى اللاعب "أ" رقمًا وحدد نقطة. في الرمية التالية، التقط اللاعب المجاور لـ"أ" (اللاعب "ب") النرد ورمى. ليس من الواضح سبب قيامه بذلك، أو إن كان يعرف "أ". اعترض أحد اللاعبين الآخرين، مشيرًا إلى أن "ب" لم يكن الرامي الأصلي. بعد نقاش طويل وحائر بين الموزعين ومسؤول الصندوق، مُرِّر النرد إلى اللاعب التالي (اللاعب "ج") الذي أنهى الجولة (وحصل في النهاية على سبعة).
هل كان هذا هو البروتوكول الصحيح في هذه الحالة، وإن كان كذلك، فما هو منطقه؟ إذا لم يرغب اللاعب "أ" في اللعب مرة أخرى لسببٍ ما، فلماذا لا يُسمح له بالتخلي عن النرد؟ إذا التقط اللاعب "ب" النرد لأنه لم يفهم اللعبة، أو إذا وضع رجل العصا النرد أمامه بالخطأ، ألا يجب أن يعود النرد إلى "أ" لإنهاء الجولة؟
سألتُ رجل العظام في nextshooter.com عن هذا الأمر. وهذا ما قاله.
إذا التقط لاعب غير الرامي الصحيح النرد وقام برميه، فيجب أن يكون ذلك بمثابة عدم استدعاء أو رمي ويجب إرجاع النرد إلى الرامي الصحيح. وعلى الرغم من أن هذا هو الحكم الصحيح بالفعل، إلا أن رجل الصندوق في بعض الحالات قد يسمح بالرمي إذا كانت النتيجة لصالح جميع اللاعبين أو معظمهم. وفي بعض الحالات، قد لا تؤثر نتيجة الرمي على أي من رهانات اللاعب (اللاعبين). أيضًا... يمكن لأي لاعب طلب إرسال النرد إلى الرامي التالي لإنهاء اليد. في مثل هذه الحالات، يمكن إرسال نفس النرد أو يمكن للرامي الجديد طلب نرد جديد. وعند اكتمال الرمي، يمكن للرامي نفسه رمي يده الخاصة، وبالتالي يكون لديه أكثر من يد.
ما احتمال الحصول على مجموع أكبر من ١٠٠ عند رمي ٢٠ نردًا؟ مع تحياتي.
بدأتُ باستخدام التقريب الطبيعي لحل هذه المسألة، لكن احتمالية تجاوز 100 نقطة منخفضة جدًا بحيث لا تكون هذه الطريقة دقيقة. لذلك، أجريتُ محاكاة عشوائية لـ 8.25 مليون تجربة، وكان عدد التجارب التي بلغت 101 نقطة أو أكثر 127. لذا، فإن الاحتمالية هي حوالي 1 من 65,000.
حان وقت سؤال آخر حول "صفقة أم لا". لنفترض، بعد كل الصفقات التي أجراها المصرفي وظهور سيلين ديون كضيفة شرف، أن يتبقى لديك حقيبتان، إحداهما بقيمة 500,000 دولار والأخرى بقيمة مليون دولار. أفترض أن عرض المصرفي سيكون أقل بقليل من 750,000 دولار. أيهما ستختار؟ ماذا لو كانت الحقيبتان المتبقيتان هما الحقيبتان اللتان تبلغ قيمتهما 0.01 دولار والأخرى بقيمة مليون دولار؟ أعتقد أن الأمر كله يتعلق بكونك مقامرًا أم لا، ولا علاقة له بالاحتمالات. سبب سؤالي هو أنني أتساءل إن كان أي شخص سيفوز بمليون دولار (حتى لو اختار الحقيبة السحرية).
عندما تصبح الجوائز مبالغ مؤثرة، ينبغي على اللاعب الحكيم أن يلعب بحذر على حساب تعظيم القيمة المتوقعة. الاستراتيجية الجيدة هي تعظيم السعادة المتوقعة. أعتقد أن دالة جيدة لقياس السعادة هي لوغاريتم إجمالي ثروتك. لنفترض أن شخصًا لديه ثروة حالية قدرها 100,000 دولار، وعُرضت عليه حالتان: 0.01 دولار و1,000,000 دولار. بقبول "عدم وجود صفقة"، تكون السعادة المتوقعة 0.5 * لوغاريتم ($100,000.01) + 0.5 * لوغاريتم ($1,100,000) = 5.520696. ليكن b هو عرض البنك الذي لا يمانع اللاعب في قبوله.
log(b) = 5.520696
ب = 10 5.520696
ب = 331,662.50 دولارًا.
لذا، يجب أن يكون هذا اللاعب الافتراضي غير مبالٍ بعرض البنك البالغ 331,662.50 دولارًا. كلما قلّت ثروتك عند بدء اللعبة، كان عليك اللعب بتحفظ أكبر. عادةً ما تكون عروض البنك في المراحل الأخيرة من اللعبة قريبة من القيمة المتوقعة، وأحيانًا أكثر بقليل. الحالة المنطقية الوحيدة التي يمكن أن يفوز فيها اللاعب بالمليون هي إذا كان لديه ثروة كبيرة عند بدء اللعبة و/أو كانت عروض البنك بخيلة بشكل غير عادي. يبدو أن المنتجين يفضلون أفراد الطبقة المتوسطة المجتهدين، لذلك من غير المرجح أن نرى شخصًا يستطيع تحمل التهاون عندما يتعلق الأمر بمبالغ كبيرة. كما أنني لم أرَ البنك يقدم عروضًا أقل من 90٪ من القيمة المتوقعة في وقت متأخر من اللعبة. الوقت الذي سنرى فيه شخصًا يفوز بالمليون هو عندما يظهر مقامر منحط في العرض ولا يمكنه التوقف. عندما يحدث ذلك، سأكون مشجعًا للمصرفي.
أعجبني موقعك! لقد عثرتُ للتو على قائمتك المفصلة لطاولات بلاك جاك لاس فيغاس ومزاياها، لذا كنتُ أتساءل: لنفترض أن هناك طاولتين بلاك جاك، إحداهما بميزة 0.2% مع حد أدنى للرهان 10 دولارات، والأخرى 0.4% مع حد أدنى للرهان 5 دولارات. كلتا الطاولتين لهما نفس نسبة الخسارة البالغة 0.02 دولار لكل يد. هل هناك أي ميزة لاختيار طاولة على الأخرى؟
شكراً. للإجابة على هذا السؤال، عليك أولاً أن تسأل نفسك لماذا تُقامر أصلاً. إذا كنت تسعى لتقليل خسارتك قدر الإمكان، فلا تلعب إطلاقاً. أما إذا كنت تلعب من أجل متعة المقامرة، فأنصحك باختيار لعبة الـ 10 دولارات مع هامش ربح 0.2%. ستكون الخسارة المتوقعة هي نفسها، ولكنك ستحصل على تعويض أكبر مع الرهانات الأكبر.
هناك رهان جانبي في لعبة باي غاو بوكر في كازينو نياجرا، يُدفع من خلال جائزة كبرى بدلًا من احتمالات ثابتة. أتساءل عن المبلغ المطلوب لتحقيق التعادل في هذا الرهان (بافتراض أن الرهان يُحدد أقصى عائد لرهان الجائزة الكبرى).
نقطة التعادل هي ١٠٢,٦٨٠.٢٤ دولارًا أمريكيًا. أضفتُ للتو تحليلًا لهذا الرهان إلى قسم الرهانات الجانبية في باي غاو بوكر .
لا أعرف الكثير عن البوكر، ولكني أجده ممتعًا، لذا ربما يمكنك توضيح شيء ما لي. في رحلة حديثة إلى لاس فيغاس مع زوجتي، أقمنا في فندق أريزونا تشارليز ديكاتور. كان سبب إقامتنا هنا هو إعلانهم عن لعبة هولدم بقيمة 2-4 دولار على موقعهم الإلكتروني. في صباح اليوم الأول، ذهبنا إلى غرفة البوكر وسجلنا أسماءنا مقابل 2-4 دولار. لاحظت أن رجل البوكر يكتب أسماءنا تحت الأعمدة مقابل 4-8 دولارات. لذلك أخبرته أننا نريد 2-4 دولار (كان هناك عمود بعنوان "2-4 دولار" على نفس الورقة). قال إنها 2-4 دولار: 2 دولار قبل الفلوب، و4 دولارات بعد الفلوب، و8 دولارات بعد الدور والنهر. وصفت له ما قصدته بـ 2-4 دولار: 2 دولار قبل وبعد الفلوب و4 دولارات بعد الدور والنهر. ضحك علينا كما لو كنا لا نعرف عما نتحدث وقال إن هذه ليست الطريقة التي تُلعب بها اللعبة. انتهى بنا المطاف بلعب البوكر في جولد كوست طوال ما تبقى من رحلتنا. هل هذا النوع من الرهانات طبيعي في غرف البوكر؟ (أخبرتُ مشرف غرفة البوكر أنه لو كان بإمكاننا تحمل تكلفة لعبة هولدم التي تتراوح بين 4 و8 دولارات، لما بقينا في أريزونا تشارليز).
أوافق على أن لعبة "2/4" تعني أن الرهانات تكون بوحدات دولارين قبل الدور و4 دولارات بعده. مع ذلك، من المرجح أن يكون الرهان الأعمى الصغير دولارًا واحدًا. يبدو أن أريزونا تشارليز عندما تُسمي اللعبة "2/4" تُشير إلى الرهانات العمياء، أي رهان أعمى صغير بقيمة دولارين، ورهان أعمى كبير بقيمة 4 دولارات، أي رهانات بقيمة 8 دولارات بعد الدور. لم أسمع بهذا الاستخدام من قبل، لذا لا ألومك على دهشتك.
ملاحظة: تلقيت لاحقًا ما يلي من أنتوني، مشرف غرفة البوكر.
أنا مشرف غرفة بوكر. كنت أكتب فقط لأطلعكم على الصياغة الصحيحة لحدود الرهان في لعبة تكساس هولدم. إذا كانت اللعبة تُسمى 2/4 دولار، فهذا يعني الرهانات. (لا يُشار إلى اللعبة بالرهانات البلايند إلا إذا كانت بلا حدود). 2 دولار قبل الفلوب وبعده، و4 دولارات في الدور والريفر. اللعبة المُدرجة بـ 2/4/8 دولارات (وهو ما أظن أن كاتب الرسالة السابق كان يقصده تحديدًا، هي 2 دولار قبل الفلوب، و4 دولارات بعد الفلوب، و8 دولارات في الدور والريفر). من الممكن أيضًا أن تكون اللعبة مُدرجة بـ 2/4/6/8 دولارات. لنقل هذه المعلومات، يُريد مشرفو البوكر الجيدون أن يحصل الناس على أكبر قدر ممكن من المعلومات.


