اسأل الساحر #284
هل سمعتَ عن وكالة السيارات في سياتل التي اضطرت لدفع 420 ألف دولار لأن فريق سيهوكس تغلب على فريق جاينتس؟ قرأتُ أنهم اضطروا لدفع 7 آلاف دولار لبوليصة التأمين ضد ذلك. ما هو القسط العادل؟
وفقًا للمقالة التي تحمل عنوان " وكالة سيارات واشنطن تدفع 420 ألف دولار بعد فوز سيهوكس على العمالقة" ، فقد أطلقت الوكالة حملة ترويجية لدفع 35 ألف دولار لكل فائز من اثني عشر لاعبًا إذا فاز سيهوكس على العمالقة في مباراة الأسبوع الخامس عشر، التي أقيمت في 15 ديسمبر 2013. وتستمر المقالة في القول إن الوكالة دفعت 7 آلاف دولار مقابل بوليصة تأمين للدفع في هذا الحدث في حالة حدوثه بالفعل.
بناءً على جميع مباريات دوري كرة القدم الأمريكية (NFL) من مواسم ١٩٨٣ إلى ٢٠١٢، كان فريقٌ مُحددٌ في أي مباراةٍ مُحددةٍ قد خسرها. مع ذلك، وبصفته فريقًا مُرشحًا للفوز بفارق سبع نقاط، وفي مباراةٍ بمتوسط نقاطٍ أعلى/أقل، أرى أن احتمالية خسارة فريق جاينتس كانت أعلى من المُتوسط. كان متوسط النقاط في تلك المباراة ٤١. لنُجرِ بعض العمليات الحسابية لإيجاد العدد المُتوقع لنقاط جاينتس.
يترك:
س=نقاط سيهوكس
g=نقاط العمالقة
نحن نعلم أن s+g=41 و s=g+7، استنادًا إلى فارق النقاط وإجمالي أكثر/أقل.
استبدال المعادلة الثانية في الأولى:
(ز+7) + ز = 41
2ج +7 = 41
2 جرام = 34
ج = 17
لنلقِ نظرةً بعد ذلك على احتمالية عدم استقبال أي هدف بناءً على العدد المُقدّر لنقاط كل فريق، استنادًا إلى مواسم 1983 إلى 2012. لقد تجاوزتُ أي صفوف كان فيها حجم العينة صفرًا.
احتمالية الإغلاق
| مُقدَّر نقاط | حجم العينة | إغلاقات | نسبة |
|---|---|---|---|
| 5.25 | 1 | 0 | 0.0% |
| 6.50 | 1 | 0 | 0.0% |
| 7.75 | 1 | 0 | 0.0% |
| 8.00 | 1 | 0 | 0.0% |
| 8.25 | 3 | 0 | 0.0% |
| 8.50 | 2 | 0 | 0.0% |
| 8.75 | 2 | 0 | 0.0% |
| 9.00 | 2 | 0 | 0.0% |
| 9.50 | 4 | 0 | 0.0% |
| 9.75 | 6 | 1 | 16.7% |
| 10.00 | 10 | 1 | 10.0% |
| 10.25 | 7 | 0 | 0.0% |
| 10.50 | 14 | 2 | 14.3% |
| 10.75 | 7 | 1 | 14.3% |
| 11.00 | 13 | 1 | 7.7% |
| 11.25 | 21 | 1 | 4.8% |
| 11.50 | 22 | 3 | 13.6% |
| 11.75 | 23 | 1 | 4.3% |
| 12.00 | 34 | 2 | 5.9% |
| 12.25 | 36 | 7 | 19.4% |
| 12.50 | 41 | 3 | 7.3% |
| 12.75 | 39 | 4 | 10.3% |
| 13.00 | 55 | 1 | 1.8% |
| 13.25 | 58 | 5 | 8.6% |
| 13.50 | 78 | 1 | 1.3% |
| 13.75 | 89 | 5 | 5.6% |
| 14.00 | 92 | 4 | 4.3% |
| 14.25 | 108 | 7 | 6.5% |
| 14.50 | 117 | 8 | 6.8% |
| 14.75 | 141 | 7 | 5.0% |
| 15.00 | 160 | 7 | 4.4% |
| 15.25 | 160 | 7 | 4.4% |
| 15.50 | 213 | 7 | 3.3% |
| 15.75 | 198 | 11 | 5.6% |
| 16.00 | 206 | 6 | 2.9% |
| 16.25 | 221 | 12 | 5.4% |
| 16.50 | 241 | 10 | 4.1% |
| 16.75 | 273 | 7 | 2.6% |
| 17.00 | 306 | 8 | 2.6% |
| 17.25 | 305 | 8 | 2.6% |
| 17.50 | 306 | 10 | 3.3% |
| 17.75 | 323 | 4 | 1.2% |
| 18.00 | 299 | 8 | 2.7% |
| 18.25 | 332 | 8 | 2.4% |
| 18.50 | 309 | 9 | 2.9% |
| 18.75 | 307 | 7 | 2.3% |
| 19.00 | 356 | 8 | 2.2% |
| 19.25 | 389 | 5 | 1.3% |
| 19.50 | 361 | 5 | 1.4% |
| 19.75 | 343 | 6 | 1.7% |
| 20.00 | 402 | 8 | 2.0% |
| 20.25 | 379 | 6 | 1.6% |
| 20.50 | 359 | 3 | 0.8% |
| 20.75 | 353 | 5 | 1.4% |
| 21.00 | 344 | 1 | 0.3% |
| 21.25 | 317 | 3 | 0.9% |
| 21.50 | 341 | 2 | 0.6% |
| 21.75 | 331 | 1 | 0.3% |
| 22.00 | 369 | 1 | 0.3% |
| 22.25 | 336 | 0 | 0.0% |
| 22.50 | 316 | 2 | 0.6% |
| 22.75 | 280 | 3 | 1.1% |
| 23.00 | 311 | 1 | 0.3% |
| 23.25 | 290 | 3 | 1.0% |
| 23.50 | 279 | 1 | 0.4% |
| 23.75 | 255 | 1 | 0.4% |
| 24.00 | 246 | 1 | 0.4% |
| 24.25 | 219 | 0 | 0.0% |
| 24.50 | 230 | 2 | 0.9% |
| 24.75 | 230 | 1 | 0.4% |
| 25.00 | 212 | 2 | 0.9% |
| 25.25 | 207 | 0 | 0.0% |
| 25.50 | 176 | 1 | 0.6% |
| 25.75 | 154 | 0 | 0.0% |
| 26.00 | 154 | 1 | 0.6% |
| 26.25 | 113 | 0 | 0.0% |
| 26.50 | 137 | 0 | 0.0% |
| 26.75 | 122 | 0 | 0.0% |
| 27.00 | 95 | 0 | 0.0% |
| 27.25 | 98 | 0 | 0.0% |
| 27.50 | 83 | 0 | 0.0% |
| 27.75 | 81 | 0 | 0.0% |
| 28.00 | 82 | 0 | 0.0% |
| 28.25 | 55 | 1 | 1.8% |
| 28.50 | 56 | 0 | 0.0% |
| 28.75 | 51 | 0 | 0.0% |
| 29.00 | 48 | 0 | 0.0% |
| 29.25 | 34 | 0 | 0.0% |
| 29.50 | 24 | 0 | 0.0% |
| 29.75 | 25 | 0 | 0.0% |
| 30.00 | 24 | 0 | 0.0% |
| 30.25 | 21 | 0 | 0.0% |
| 30.50 | 18 | 0 | 0.0% |
| 30.75 | 23 | 0 | 0.0% |
| 31.00 | 16 | 0 | 0.0% |
| 31.25 | 15 | 0 | 0.0% |
| 31.50 | 8 | 0 | 0.0% |
| 31.75 | 3 | 0 | 0.0% |
| 32.00 | 6 | 0 | 0.0% |
| 32.25 | 7 | 0 | 0.0% |
| 32.50 | 6 | 0 | 0.0% |
| 32.75 | 3 | 0 | 0.0% |
| 33.00 | 4 | 0 | 0.0% |
| 33.25 | 6 | 0 | 0.0% |
| 33.50 | 5 | 0 | 0.0% |
| 34.75 | 4 | 0 | 0.0% |
| 35.00 | 2 | 0 | 0.0% |
| 35.50 | 1 | 0 | 0.0% |
| 36.00 | 2 | 0 | 0.0% |
| 36.25 | 1 | 0 | 0.0% |
| 36.50 | 1 | 0 | 0.0% |
| 37.25 | 1 | 0 | 0.0% |
| 37.75 | 2 | 0 | 0.0% |
| 42.25 | 1 | 0 | 0.0% |
الخطوات التالية معقدة للغاية بحيث لا يمكن شرحها هنا، ولكنني طورت صيغة لاحتمالية عدم تسجيل أي هدف، بالنظر إلى عدد النقاط المقدرة.
p = النقاط المقدرة.
x = 1.562545 -0.302485 * ص
احتمالية الإغلاق = e x /(1+e x )
يوضح الرسم البياني التالي الاحتمال الفعلي والمقدر للفوز بشباك نظيفة بفارق يتراوح بين 14 إلى 22 نقطة.
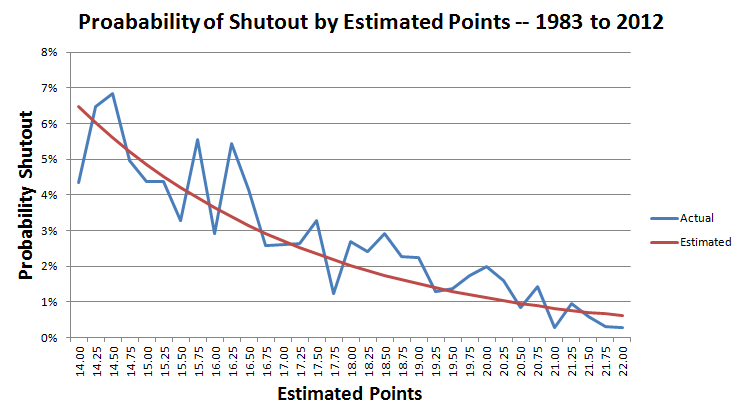
وفي المباراة المذكورة كان من المتوقع أن يسجل العمالقة 17 نقطة.
باستخدام الصيغة الموجودة أعلى الجدول:
x = 1.562545 -0.302485 * 17 = -3.579706
احتمالية الفوز = exp(-3.579706)/(exp(-3.579706)+1) = 2.71%. بالتحديد، 0.0271275.
بما أن الوكالة كانت ستضطر لدفع 420,000 دولار في حال فوز فريق جاينتس 1-0، فإن التكلفة العادلة للوثيقة ستكون 420,000 دولار × 0.0271275 = 11,394 دولارًا. عادةً، تضاعف شركات التأمين التي تُؤمّن عروضًا ترويجية غير اعتيادية كهذه التكلفة العادلة، لذا كنت أتوقع قسطًا قدره 22,788 دولارًا. لذا، كان قسط التأمين الذي دفعته الوكالة والبالغ 7,000 دولار صفقة رابحة. بافتراض أن المدير سيراجع الحسابات، لا أريد أن أكون مكان من حسب قسط التأمين البالغ 7,000 دولار.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
ما هو الدليل على عدم وجود أكبر عدد أولي؟
لنفترض، ولو للحظة، أن هناك أكبر عدد أولي. يمكننا ترقيم الأعداد الأولية p1=2، p2=3، p3=5، p4=7، ... pL = أكبر عدد أولي.
الآن دعنا نحدد الرقم x = p1*p2*p3*p4*...*pL + 1.
ما يعنيه أن يكون العدد أوليًا هو أنه لا يمكن تقسيم أي عدد أولي أصغر منه بالتساوي.
إذا قسمنا p1، p2، p3، ... pL على x نحصل على باقي 1 في كل مرة.
قد تجادل بأن عددًا أوليًا أكبر من pL ينقسم إلى x بالتساوي. نعم، ولكنك ستجد حينها عددًا أوليًا أكبر مما يُسمى أكبر عدد أولي. وإلا، فإن x يصبح أكبر عدد أولي جديد، مما يُثبت التخمين الأولي بوجود أكبر عدد أولي بالتناقض.
تم طرح هذا السؤال ومناقشته في المنتدى الخاص بي في Wizard of Vegas .
هل تتفق مع المقال الذي يحمل عنوان"الرياضيات تقول أنه يجب عليك شراء تذكرة Mega Millions الآن " في Business Insider؟
لا، لا أتفق معه. هذا مقال صحفي سيء، ويجب على بيزنس إنسايدر أن يشعر بالحرج منه.
بدايةً، نُشر المقال في ١٧ ديسمبر ٢٠١٣، قبل سحب اليانصيب على جائزة الـ ٦٣٦ مليون دولار في ذلك المساء. لنلقِ نظرة على الحسابات لتقييم قيمة تذكرة بقيمة دولار واحد. يوضح الجدول التالي احتمالية وعائد جميع النتائج المحتملة للجائزة الكبرى البالغة ٦٣٦ مليون دولار، قبل الأخذ في الاعتبار عوامل مثل غرامة المبلغ الإجمالي، والضرائب، وتقاسم الجائزة الكبرى. الاحتمالات الثلاثة الأولى مُعدّة علميًا نظرًا لصغر حجمها.
ميجا ميليونز - جائزة كبرى بقيمة 636 مليون دولار
| يمسك | الكرة الضخمة | يدفع | التركيبات | احتمال | يعود |
|---|---|---|---|---|---|
| 5 | نعم | 636,000,000 دولار | 1 | 3.86E-09 | 2.456634 |
| 5 | لا | مليون دولار | 14 | 5.41E-08 | 0.054077 |
| 4 | نعم | 5000 دولار | 350 | 1.35E-06 | 0.006760 |
| 4 | لا | 500 دولار | 4,900 | 0.000019 | 0.009463 |
| 3 | نعم | 50 دولارًا | 24,150 | 0.000093 | 0.004664 |
| 3 | لا | 5 دولارات | 338,100 | 0.001306 | 0.006530 |
| 2 | نعم | 5 دولارات | 547,400 | 0.002114 | 0.010572 |
| 1 | نعم | 2 دولار | 4,584,475 | 0.017708 | 0.035416 |
| 0 | نعم | 1 دولار | 12,103,014 | 0.046749 | 0.046749 |
| الخاسر | 0 دولار | 241,288,446 | 0.932008 | 0.000000 | |
| المجموع | 258,890,850 | 1.000000 | 2.630865 | ||
هذا يُظهر أن تذكرة بقيمة دولار واحد ستُعاد إليها ٢٫٦٣٠٨٦٤ دولارًا. بعد خصم تكلفة التذكرة، يكون الربح المتوقع ١٫٦٣٠٨٦٤ دولارًا. يحصل موقع Business Insider على ١٫٦٣٢٠٢٩ دولارًا. الفرق هو ٠٫٠٠١١٦٤ دولارًا، ولكن ليس بالأمر المهم.
ومع ذلك، هناك ثلاثة أشياء تؤدي إلى انخفاض القيمة بشكل كبير:
- غرامة المبلغ الإجمالي.
- الضرائب.
- مشاركة الجائزة الكبرى.
دعونا ننظر إليهم واحدا تلو الآخر.
تُدفع عادةً جوائز اليانصيب الكبرى التراكمية على شكل معاش سنوي لمدة 30 عامًا تقريبًا، بما في ذلك جوائز ميجا مليونز. إذا أراد الفائز الحصول على كامل المبلغ دفعةً واحدة، وهو ما يرغب به معظم الناس، فعليه قبول تخفيض كبير. وهذا أمرٌ عادل، لأن قيمة الدولار اليوم تفوق قيمة الدولار في المستقبل. في حالة سحب 17 ديسمبر 2013، خُفِّض إجمالي قيمة الجائزة إلى 347.6 مليون دولار، أي ما يعادل 54.65% من قيمة الجائزة الكبرى المعلن عنها.
لنلقِ نظرة على الضرائب. أعلى معدل ضريبة دخل هامشية اتحادي هو 39.6%. تتراوح ضرائب الولايات بين 0% و12.3%، أي 6% فقط في المتوسط. بعد خصم 45.6% من الضرائب، يتبقى لدينا 189.1 مليون دولار.
الآن يأتي الجزء الأصعب - مشاركة الجائزة الكبرى. تجدر الإشارة إلى أنه بدءًا من سحب Mega Millions في 22 أكتوبر 2013، غيّرت القواعد إلى تنسيق 75-15، حيث يسحبون خمسة أرقام من 1 إلى 75، ثم رقم واحد من مجموعة منفصلة من 1 إلى 15. وقد قلل هذا من احتمالات الفوز إلى 1 من 258,890,850، ومن الواضح أن ذلك كان في محاولة للحصول على جوائز كبرى أكبر. بالنظر إلى 17 سحبًا فقط منذ ذلك الحين، باستخدام بيانات الجائزة الكبرى والمبيعات من LottoReport.com ، أجد أن هناك علاقة أسية بين حجم الجائزة الكبرى والطلب. لقد وجدت الشيء نفسه بالنسبة ليانصيب Powerball ، بالمناسبة. باستخدام الانحدار الأسي، تكون صيغتي لإجمالي التذاكر المباعة (بالملايين) 12.422 × exp(0.0052 × j)، حيث j هو حجم الجائزة الكبرى (بالملايين). على سبيل المثال، لجائزة كبرى بقيمة 636 مليون دولار، ستكون المبيعات المتوقعة 12.422 × exp(0.0052*636) = 339.2 مليون دولار. أما المبيعات الفعلية، فكانت 337 مليون دولار، أي أنها قريبة جدًا.
بناءً على مبيعات التذاكر الفعلية البالغة 336,545,306، يمكننا توقع 336,545,306/258,890,850 = 1,300 فائز. السؤال المهم هو: إذا فزت، فكم عدد الأشخاص الآخرين الذين تتوقع أن تتقاسم معهم الجائزة؟ الإجابة سهلة باستخدام توزيع بواسون. بافتراض أن متوسط عدد الفائزين هو 1.3 فائز، فإن احتمالية وجود عدد محدد من الفائزين هي exp(1.3)×1.3 x /fact(x). يوضح الجدول التالي احتمالية وجود من 0 إلى 10 فائزين آخرين، وحصتك من الجائزة الكبرى في كل حالة، والحصة المتوقعة، بافتراض فوزك.
حصة الجائزة الكبرى المتوقعة تُمنح لـ 1.3 فائز آخر في المتوسط
| الفائزون الآخرون | احتمال | حصة الجائزة الكبرى | الحصة المتوقعة |
|---|---|---|---|
| 10 | 0.000001 | 0.090909 | 0.000000 |
| 9 | 0.000008 | 0.100000 | 0.000001 |
| 8 | 0.000055 | 0.111111 | 0.000006 |
| 7 | 0.000339 | 0.125000 | 0.000042 |
| 6 | 0.001827 | 0.142857 | 0.000261 |
| 5 | 0.008431 | 0.166667 | 0.001405 |
| 4 | 0.032429 | 0.200000 | 0.006486 |
| 3 | 0.099786 | 0.250000 | 0.024946 |
| 2 | 0.230283 | 0.333333 | 0.076761 |
| 1 | 0.354295 | 0.500000 | 0.177148 |
| 0 | 0.272545 | 1.000000 | 0.272545 |
| المجموع | 1.000000 | 0.559602 |
تُظهر الخلية الموجودة في أسفل اليمين أنك قد تتوقع الاحتفاظ بنسبة 55.96% من الأموال، وستذهب النسبة الأخرى البالغة 44.04% إلى هؤلاء الفائزين الآخرين الذين سيتعين عليك تقاسمها معهم.
الآن، انخفضت قيمة جائزتنا الكبرى البالغة 636 مليون دولار إلى 189.1 × 55.96% = 105.8 مليون دولار. لنرَ كيف سيبدو جدول العائدات مع هذا الرقم كجائزة كبرى.
ميجا ميليونز - جائزة كبرى بقيمة 105.8 مليون دولار
| يمسك | الكرة الضخمة | يدفع | التركيبات | احتمال | يعود |
|---|---|---|---|---|---|
| 5 | نعم | 105,800,000 دولار | 1 | 3.86E-09 | 0.408666 |
| 5 | لا | مليون دولار | 14 | 5.41E-08 | 0.054077 |
| 4 | نعم | 5000 دولار | 350 | 1.35E-06 | 0.006760 |
| 4 | لا | 500 دولار | 4,900 | 0.000019 | 0.009463 |
| 3 | نعم | 50 دولارًا | 24,150 | 0.000093 | 0.004664 |
| 3 | لا | 5 دولارات | 338,100 | 0.001306 | 0.006530 |
| 2 | نعم | 5 دولارات | 547,400 | 0.002114 | 0.010572 |
| 1 | نعم | 2 دولار | 4,584,475 | 0.017708 | 0.035416 |
| 0 | نعم | 1 دولار | 12,103,014 | 0.046749 | 0.046749 |
| الخاسر | 0 دولار | 241,288,446 | 0.932008 | 0.000000 | |
| المجموع | 258,890,850 | 1.000000 | 0.582898 | ||
تُظهر الخلية أسفل اليمين عائدًا متوقعًا بنسبة 58.29%. بمعنى آخر، يُمكنك توقع عائد استثمارك البالغ دولارًا واحدًا بحوالي 58 سنتًا، مع خسارة متوقعة، أو ميزة كازينو، تبلغ حوالي 42%. هل يبدو هذا منطقيًا، إذًا، يجب عليك شراء تذكرة؟
وفقًا للمقال، "لذا، طالما أن عدد التذاكر المباعة أقل من 730 مليون تذكرة، وهو وضع محتمل إلى حد ما في الوقت الحالي، فإن القيمة المتوقعة للتذكرة يجب أن تكون إيجابية، ولذلك يجب أن تفكر في شراء تذكرة ميجا ميليونز اليوم."
كانت المبيعات أقل بكثير من 730 مليونًا، ومع ذلك، كانت قيمةً زهيدة. مع ذلك، وللإنصاف، أضاف المقال ما يلي:
ضع في اعتبارك أن هناك العديد من المحاذير لهذا التحليل. من المرجح أن تؤثر الضرائب سلبًا على أرباحك المتوقعة - ستأخذ الحكومة الفيدرالية حوالي 40%، وستطالب ولايتك الأصلية بنسبة تتراوح بين 0% و13% تقريبًا.
لقد قام الكثير من الناس بشراء التذاكر، وكما ناقشنا أعلاه، فإن هذا من شأنه أن يزيد بشكل كبير من احتمالات التعادل، وبالتالي تقليل العائد الذي يصاحب ذلك.
هذه بعض التحذيرات المهمة! لا ينبغي ذكرها بشكل عابر في نهاية التقرير، بل يجب أخذها في الاعتبار عند التحليل من البداية.
ليس أنك سألت، ولكنني أجد أن الحسابات الرياضية تُشير إلى أنه لا يجب عليك لعب ميجا مليونز أبدًا. نظرًا للطلب المتزايد على التذاكر، وبناءً على حجم الجائزة الكبرى، أجد أن الوقت الأمثل للعب هو جائزة كبرى قدرها 545 مليون دولار. مع جوائز كبرى أكبر من ذلك، ستضطر لمشاركتها مع عدد كبير جدًا من الفائزين الآخرين. بهذا الحجم، يمكن للاعب توقع عائد بنسبة 60.2%، أو خسارة بنسبة 39.8%. هذا أفضل ما يمكن توقعه.
وفي الختام، لا، أنا لا أتفق مع ما ذهب إليه موقع Business Insider في خداع القراء بعنوان مثير وعدم إجراء تحليل سليم للضرائب وتقاسم الجوائز الكبرى.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .


