اسأل الساحر #313
ما هو التباين في كليوباترا كينو ؟
كتذكير لقرائنا الآخرين، تُلعب لعبة كليوباترا كينو كلعبة كينو تقليدية، إلا أنه إذا تطابقت آخر كرة مسحوبة مع أحد اختيارات اللاعب وحققت فوزًا، فسيفوز اللاعب أيضًا بـ ١٢ لعبة مجانية بمضاعف ٢x. الألعاب المجانية لا تُكسب المزيد من الألعاب المجانية.
لم تُحدد عدد مرات الالتقاط أو جدول الأجور، لذا لنستخدم جدول الأجور 3-10-56-180-1000 لاختيار 8 كمثال. أولًا، لنحسب العائد.
عدد طرق التقاط x كرة من y في لعبة الكينو هو عدد طرق اختيار x كرة من 20 وyx من 60. هذا يساوي combin(20,x)*combin(60,yx)، وذلك بصيغة Excel. وللتذكير، combin(x,y) = x!/(y!*(xy)!). وأخيرًا، x! = 1*2*3*...*x.
بعد هذه المراجعة، إليكم جدول العائدات لجدول الأرباح. يُظهر العمود الأيمن مربع الربح المتوقع، والذي سنحتاجه لاحقًا.
اختر 8 كينو
| حدث | يدفع | التركيبات | احتمال | يعود | العودة^2 |
|---|---|---|---|---|---|
| 0 | 0 | 2,558,620,845 | 0.088266 | 0.000000 | 0.000000 |
| 1 | 0 | 7,724,138,400 | 0.266464 | 0.000000 | 0.000000 |
| 2 | 0 | 9,512,133,400 | 0.328146 | 0.000000 | 0.000000 |
| 3 | 0 | 6,226,123,680 | 0.214786 | 0.000000 | 0.000000 |
| 4 | 3 | 2,362,591,575 | 0.081504 | 0.244511 | 0.733533 |
| 5 | 10 | 530,546,880 | 0.018303 | 0.183026 | 1.830259 |
| 6 | 56 | 68,605,200 | 0.002367 | 0.132536 | 7.422014 |
| 7 | 180 | 4,651,200 | 0.000160 | 0.028882 | 5.198747 |
| 8 | 1000 | 125,970 | 0.000004 | 0.004346 | 4.345661 |
| المجموع | 28,987,537,150 | 1.000000 | 0.593301 | 19.530214 |
الآن، لنحسب متوسط المكافأة. يتضح من الجدول أعلاه أن متوسط الربح، دون احتساب المكافأة، هو 0.593301. يحصل اللاعب في هذه المكافأة على 12 دورة مجانية مضاعفة. وبالتالي، فإن الربح المتوقع من المكافأة هو 2 × 12 × 0.593301 = 14.239212.
الآن، لنحسب احتمال الفوز بالمكافأة. إذا التقط اللاعب أربعة أرقام، فإن احتمال أن تكون الكرة العشرون واحدة منها هو 4/20. عمومًا، إذا التقط اللاعب الرقم c، فإن احتمال أن تكون الكرة العشرون قد ساهمت في الفوز هو c/20.
صيغة الفوز بالمكافأة هي احتمال (الفرصة الرابعة) * (4/20) + احتمال (الفرصة الخامسة) * (5/20) + احتمال (الفرصة السادسة) * (6/20) + احتمال (الفرصة السابعة) * (7/20) + احتمال (الفرصة الثامنة) * (8/20). نعرف احتمال أي فوز من جدول العائدات أعلاه. لذا، فإن احتمال الفوز بالمكافأة هو:
0.081504*(4/20) + 0.018303*(5/20) + 0.002367*(6/20) + 0.000160*(7/20) + 0.000004*(8/20) = 0.021644.
وباستخدام احتمالية الفوز بالمكافأة ومتوسط الفوز بالمكافأة، يمكننا حساب العائد من المكافأة على النحو التالي: 0.021644 × 14.239212 = 0.308198.
ليس أننا بحاجة إلى معرفة ذلك، ولكن العائد الإجمالي للعبة هو العائد من اللعبة الأساسية بالإضافة إلى العائد من المكافأة، وهو ما يساوي 0.593301 + 0.308198 = 0.901498.
لنبدأ الآن بشرح التباين الفعلي. للتذكير، الصيغة العامة للتباين هي:
var(x + y) = var(x) + var(y) + 2*cov(x,y)، حيث var تعني التباين وcov تعني التغاير. في هذه الحالة:
التباين الإجمالي = var(اللعبة الأساسية) + var(المكافأة) + 2*cov(اللعبة الأساسية والمكافأة).
الصيغة الأساسية للتباين هي E(x^2) - [E(x)]^2. بمعنى آخر، مربع الربح المتوقع مطروحًا منه مربع الربح المتوقع.
مع ذلك، لنبدأ بتباين اللعبة الأساسية. تذكروا عندما ذكرتُ سابقًا متى نحتاج إلى مربع الفوز المتوقع من الجدول الأول. تُظهر لنا الخلية السفلية اليمنى من الجدول الأول أن مربع الفوز المتوقع هو 19.530214. نعلم بالفعل أن الفوز المتوقع هو 0.593301. وبالتالي، فإن تباين اللعبة الأساسية هو 19.530214 - 0.593301 ² = 19.178208.
الآن، لنحسب تباين المكافأة (بافتراض أنها مُحققة بالفعل). لذلك، تذكر ما يلي:
var(ax) = a 2 x، حيث a هو ثابت.
وتذكر أيضًا أن تباين n متغير عشوائي x هو nx.
مع ذلك، إذا كان x هو الربح الأساسي في لعبة المكافأة، فإن تباين المكافأة بأكملها يساوي 2 × 12 × x. نعلم من المعادلة السابقة أن تباين دورة واحدة في اللعبة الأساسية، دون احتساب المكافأة، يساوي 19.178208. لذا، فإن تباين المكافأة، بشرط الحصول على مكافأة بالفعل، هو 2 × 12 × 19.178208 = 920.554000.
مع ذلك، ما نحتاج معرفته هو تباين المكافأة قبل سحب الكرة الأولى، بما في ذلك احتمال عدم الفوز بها إطلاقًا. لا، لا يمكننا ببساطة ضرب تباين المكافأة في احتمال الفوز بها. بدلًا من ذلك، تذكر أن var(x) = E(x^2) - [E(x)]^2. لنعد ترتيب ذلك إلى:
E(x^2) = var(x) + [E(x)]^2
نحن نعلم المتوسط والتباين للمكافأة، لذا فإن مربع الفوز المتوقع في المكافأة هو 920.554000 + 19.178208 2 = 1123.309169.
وبالتالي، فإن مربع الفوز المتوقع من المكافأة، قبل سحب الكرة الأولى، هو prob(bonus) × E(x^2) = 0.021644 × 1123.309169 = 24.313239.
لقد حسبنا بالفعل الربح المتوقع من المكافأة قبل الكرة الأولى، وهو 0.308198. وبالتالي، فإن التباين الإجمالي للمكافأة قبل الكرة الأولى هو 24.313239 - 0.308198 2 = 24.218253.
الخطوة التالية هي حساب التباين. قد تتساءل: "لماذا يوجد ارتباط بين الفوز الأساسي والفوز الإضافي؟". ذلك لأن آخر كرة مسحوبة يجب أن تُسهم في الفوز لتفعيل المكافأة. وبما أن الكرة الأخيرة ساهمت في الفوز، فإن متوسط الفوز يرتفع. للتذكير، تنص صيغة بايز لاحتمالية الشرط على ما يلي:
P(A معطاة B) = P(A و B)/P(B).
دعونا الآن نعيد عمل جدول الإرجاع للعبة الأساسية، مع الأخذ في الاعتبار أن الكرة الأخيرة كانت ضربة:
اختر 8 كينو بناءً على آخر كرة تم ضربها
| حدث | يدفع | التركيبات | احتمال | يعود |
|---|---|---|---|---|
| 0 | 0 | - | 0.000000 | 0.000000 |
| 1 | 0 | - | 0.000000 | 0.000000 |
| 2 | 0 | - | 0.000000 | 0.000000 |
| 3 | 0 | - | 0.000000 | 0.000000 |
| 4 | 3 | 472,518,315 | 0.753119 | 2.259358 |
| 5 | 10 | 132,636,720 | 0.211402 | 2.114019 |
| 6 | 56 | 20,581,560 | 0.032804 | 1.837010 |
| 7 | 180 | 1,627,920 | 0.002595 | 0.467036 |
| 8 | 1000 | 50,388 | 0.000080 | 0.080310 |
| المجموع | 627,414,903 | 1.000000 | 6.757734 |
تُظهر الخلية الموجودة في أسفل اليمين أنه بافتراض أن الكرة الأخيرة كانت ضربة، فإن متوسط الفوز هو 6.757734.
بعد ذلك، تذكر من درس الإحصاء في جامعتك أن:
cov(x,y) = exp(xy) - exp(x)*exp(y) .
في حالتنا، لنفترض أن x = الفوز الأساسي في اللعبة، وy = الفوز الإضافي. لنبدأ بـ exp(xy).
Exp(xy) = احتمال (المكافأة المربحة) * (متوسط الفوز في المباراة الأساسية مع مكافأة الفوز) * متوسط (الفوز بالمكافأة) + احتمال (عدم الفوز بالمكافأة) * (متوسط الفوز في المباراة الأساسية مع مكافأة الفوز) * متوسط (الفوز بالمكافأة مع مكافأة الفوز). من السهل القول إن متوسط (الفوز بالمكافأة مع مكافأة الفوز) = 0، لذا يُمكننا إعادة صياغته كالتالي:
Exp(xy) = احتمال (المكافأة التي تم ربحها) * (متوسط الفوز في اللعبة الأساسية مع المكافأة التي تم ربحها) * متوسط (الفوز بالمكافأة) =
0.021644 × 6.757734 × 14.239212 = 2.082719.لقد قمنا بالفعل بحل E(x) و E(y)، لذا فإن التباين هو:
cov(x,y) = exp(xy) - exp(x)*exp(y) = 2.082719 - 0.593301 × 0.308198 = 1.899865.
دعونا نعود إلى المعادلة الإجمالية للتباين عندما يتعلق الأمر بالتغاير:
التباين الكلي = var(اللعبة الأساسية) + var(المكافأة) + 2*cov(اللعبة الأساسية والمكافأة) = 19.178208 + 24.218253 + 2×1.899865 = 47.196191. الانحراف المعياري هو الجذر التربيعي لذلك، وهو 6.869948.
حسناً، هذا كل ما في الأمر. استغرق مني هذا ساعات، لذا آمل أن تكون سعيداً.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
سمعتُ أن احتمالية انتهاء الزواج بالطلاق، والتي تُقدّر عادةً بنسبة ٥٠٪ في الولايات المتحدة، تُحسب بقسمة عدد حالات الطلاق على عدد الزيجات في نفس الفترة الزمنية. هل هذا صحيح؟ هل تعتقد أن هذه طريقة عادلة لحساب هذه الإحصائية؟ أشك في ذلك لأنك تنظر إلى حالات الطلاق خلال فترة قصيرة مقارنةً بالزيجات التي استمرت لفترة طويلة.
إذا كان توزيع السكان والعمر مستقراً، وإذا كانت احتمالية الطلاق 50% حقاً، فإننا نتوقع أن نرى نسبة طلاق واحد إلى زواجين في أي فترة زمنية معينة، نظراً لحجم العينة الكبير.
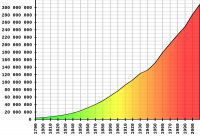
مع ذلك، فإن عدد السكان ليس مستقرًا. من هذا الرسم البياني، يبدو أن عدد سكان الولايات المتحدة ينمو بنسبة 10.71% كل عقد، أي ما يعادل 1.02% سنويًا. لنفترض 1% فقط لتبسيط الأمر.
مصدر الخريطة: تعداد الولايات المتحدة
وفقًا لموقع fatherly.com ، يبلغ متوسط مدة الزواج غير الناجح 8 سنوات.
إذا كنت تلاحظ نسبة 1 إلى 2 من حالات الطلاق إلى الزواج في الوقت الحاضر، ما هو متوسط احتمال انتهاء أي زواج معين بالطلاق؟
حالات الطلاق التي نشهدها الآن كانت من زيجات قبل ثماني سنوات، عندما كانت نسبة السكان 92.35% مما هي عليه الآن. تشير عملية حسابية بسيطة إلى أن الاحتمال الحقيقي للطلاق هو 54.14%.
دعونا نتحقق من ذلك.
أولاً، وفقًا لمراكز السيطرة على الأمراض والوقاية منها، يبلغ معدل الزواج 6.9 لكل 1000 حالة زواج سنويًا. هذا الرقم لا علاقة له بالسؤال المطروح، ولكنه يساعد على فهم الأرقام المعنية.
لنفترض أن عدد السكان قبل ثماني سنوات كان 300 مليون نسمة. هذا يعني 0.69% × 300 مليون = 2,070,000 حالة زواج في تلك السنة.
إذا انتهى 54.14% منهم بالطلاق بعد ثماني سنوات، فإننا سنرى 2,070,000 * 54.14% = 1,120,698 حالة طلاق في الوقت الحاضر.
1,120,698 / 2,070,000 = 50% نسبة حالات الطلاق إلى حالات الزواج في الوقت الحاضر.
حتى لا يجادل أحد، نعم، أعلم أن حالات الطلاق لا تنتهي جميعها خلال ثماني سنوات بالضبط. ومع ذلك، بالنظر إلى كل شيء، أقول إن النتيجة النهائية لن تكون بعيدة عن نسبة الطلاق الحقيقية التي أتوقعها، وهي 54.14%.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
يُجري مكتبك، الذي يضم مئة موظف، تبادل هدايا "بابا نويل السري". في هذه المسابقة، تكتب أسماء كل شخص على أوراق منفصلة، وتضعها في قبعة، ثم يسحب كل شخص اسمًا عشوائيًا ليقدم له هدية.
السؤال هو: كم عدد الحلقات المغلقة في المتوسط؟ على سبيل المثال، في حلقة مغلقة، يُعطي جوردون لدون، الذي يُعطي لجون، الذي يُعطي لناثان، الذي يُعطي لجوردون. أو سحب اسمك.
تخيل أن كل شخص يختار واحدًا تلو الآخر. عند اختيار كل شخص، سيكون هناك نوعان من المواقف:
- لقد تم اختيار اسم الشخص الذي يقوم بالقطف بالفعل.
- اسم الشخص الذي يقوم بالتقاط الصورة لا يزال موجودًا في سلة الأسماء.
بالنسبة لأي أداة اختيار معينة، لنفترض أن هناك n شخصًا متبقيًا للاختيار.
إذا كان اسم الشخص الذي يختار قد تم اختياره بالفعل، فهناك احتمال 1/n أن يختار إغلاق حلقة تتضمن اسمه. على سبيل المثال، لنفترض أن آمي تختار. اسم آمي موجود بالفعل لدى بوب، واسم بوب موجود بالفعل لدى تشارلي، واسم تشارلي لا يزال في سلة المهملات. بوجود n اسم لا يزال في سلة المهملات، هناك احتمال 1/n أن تختار آمي اسم تشارلي، مما يُغلق حلقة.
إذا لم يتم اختيار اسم الشخص الذي يقوم بالتقاط الصورة بالفعل، فهناك فرصة 1/n لأن تختار إيمي اسمها، مما يؤدي إلى إغلاق الحلقة.
على أي حال، إذا لم تُغلق المُلتقطة حلقة، فهي تُشارك في جزء من سلسلة أخرى، والتي سيُغلقها شخص آخر في النهاية. يجب احتساب كل سلسلة مرة واحدة فقط عند إغلاقها.
وبالتالي فإن الإجابة هي 1/100 + 1/99 + 1/98 + ... + 1/1 =~ 5.187377518.
التقدير لأي عدد كبير بما فيه الكفاية من اللاعبين، n، هو ln(n).
تم طرح السؤال ومناقشته في المنتدى الخاص بي في Wizard of Vegas .
ما هو المبلغ الذي ستكون عليه قيمة البرية الإضافية المضمونة في لعبة ماكينة القمار بالفيديو؟
يعتمد ذلك على عوامل كثيرة. سأفسر سؤالك على النحو التالي: ما قيمة الرمز البري الإضافي الذي يزيد عن متوسط الرقم الذي يحصل عليه اللاعب عادةً؟ مع أن الإجابة ستختلف اختلافًا كبيرًا من لعبة لأخرى، إلا أن عاملًا مهمًا هو عدد الصفوف على الشاشة. إذا كان هناك ثلاثة صفوف، فإن الرمز البري الإضافي سيؤثر على ثلث خطوط الدفع. وبالمثل، إذا كان هناك أربعة صفوف، فستقل قيمته، ويؤثر على ربع خطوط الدفع.
للإجابة على سؤالك، اطلعتُ على لعبة كليوباترا ، التي قمتُ بتحليلها. يوضح الجدول التالي الزيادة في القيمة المتوقعة لرمز بديل، مقارنةً بعدد عشوائي من رموز البديل.
قيمة Extra Wild في كليوباترا
| بكرة | 3 صفوف | 4 صفوف |
|---|---|---|
| 1 | 95.71% | 71.79% |
| 2 | 99.76% | 74.82% |
| 3 | 76.24% | 57.18% |
| 4 | 21.25% | 15.93% |
| 5 | 1.96% | 1.47% |