يوصي المعالج
-
$مكافأة ترحيبية بقيمة 11000 -
مكافأة ترحيبية 100% -
$مكافأة ترحيبية بقيمة 3000
اسأل الساحر #318
ما هي أفضل استراتيجية للعب لعبة Race على السعر الصحيح، على افتراض أن اللاعب ليس لديه فكرة عن أسعار الجوائز؟
ولمصلحة القراء الذين ليسوا على دراية باللعبة، إليكم مقطع فيديو لها.
أعتقد أن الاستراتيجية التالية تُنتج متوسطًا أدنى لعدد الأدوار. هناك العديد من الاستراتيجيات التي تُعادلها، لكنني لا أعتقد أن أيًا منها يُمكن أن يُنافسها.
لاستخدام الاستراتيجية، قم بتسمية علامات الأسعار الأربعة بالأرقام 1 و2 و3 و4. ضعها على الجوائز الأربع وفقًا لسجل عدد الجوائز التي حصلت عليها بشكل صحيح في الماضي، بدءًا من الدور الأول على اليسار.
استراتيجية لعبة السباق
| تاريخ | الجائزة 1 | الجائزة 2 | الجائزة 3 | الجائزة 4 |
|---|---|---|---|---|
| لا أحد | 1 | 2 | 3 | 4 |
| 0 | 2 | 1 | 4 | 3 |
| 0,0 | 3 | 4 | 2 | 1 |
| 0,0,0 | 4 | 3 | 1 | 2 |
| 0,0,2 | 3 | 4 | 1 | 2 |
| 0,0,2,0 | 4 | 3 | 2 | 1 |
| 0,2 | 2 | 3 | 4 | 1 |
| 0,2,0 | 4 | 1 | 2 | 3 |
| 0,2,1 | 2 | 4 | 1 | 3 |
| 0,2,1,0 | 3 | 1 | 4 | 2 |
| 1 | 1 | 3 | 4 | 2 |
| 1,0 | 2 | 4 | 3 | 1 |
| 1,0,0 | 3 | 1 | 2 | 4 |
| 1,0,0,0 | 4 | 2 | 1 | 3 |
| 1,1 | 1 | 4 | 2 | 3 |
| 1,1,0 | 2 | 3 | 1 | 4 |
| 1,1,0,0 | 3 | 2 | 4 | 1 |
| 1,1,0,0,0 | 4 | 1 | 3 | 2 |
| 2 | 2 | 1 | 3 | 4 |
| 2,0 | 1 | 2 | 4 | 3 |
| 2,1 | 1 | 3 | 2 | 4 |
| 2,1,0 | 4 | 2 | 3 | 1 |
| 2،1،1 | 1 | 4 | 3 | 2 |
| 2,1,1,0 | 3 | 2 | 1 | 4 |
يوضح الجدول التالي احتمالية استغراق ترتيب بطاقات الأسعار الأربعة من 1 إلى 5 دورات من أصل 24 طريقة ممكنة.
عدد الأدوار المطلوبة
| المنعطفات | رقم | احتمال |
|---|---|---|
| 1 | 1 | 4.17% |
| 2 | 4 | 16.67% |
| 3 | 8 | 33.33% |
| 4 | 9 | 37.50% |
| 5 | 2 | 8.33% |
| المجموع | 24 | 100.00% |
إذا أخذنا حاصل الضرب النقطي، فإن متوسط عدد الدورات المطلوبة، بموجب هذه الاستراتيجية، هو 3.29167.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
في حلقة 18 سبتمبر 2019 من برنامج "جيوباردي"، كان هناك تصنيف بعنوان "وصف لعبة الكازينو". أحد الأدلة كان: "مرتدي ملابس أنيقة ويلعب حتى الـ 9؛ ساعات عمل المصرفي؛ ما الذي جاء بك إلى موناكو يا سيد بوند؟"
الإجابة المُقدّمة كانت "باكارا"، والتي اعتُبرت صحيحة. ألم يكن بوند يلعب لعبة "الشمان دي فير"؟
نعم، كان بوند يلعب لعبة "الشوم دو فير" بالفعل، وليس الباكارات . للتذكير، الاختلافات الرئيسية هي:
- يدور دور المصرف حول الطاولة. يتولى لاعب المصرف تلقائيًا يد المصرف*.
- يتمتع كل من اللاعب* والمصرفي بحرية الإرادة في سحب بطاقة ثالثة، طالما لا يمتلك أي منهما بطاقتين طبيعيتين من النوع 8 أو 9.
ملحوظة:
كما هو الحال عادة، عندما أكتب عن الباكارات أو الشمان دو فير، أقوم بكتابة أسماء الرهانات بأحرف كبيرة، لتجنب الخلط مع اللاعبين الذين يلعبون اللعبة.
ومع ذلك، فإن المشهد الأول من هذا القبيل موجود في مقطع دكتور نو أدناه، حيث لا يدور البنك فحسب، بل يتمتع اللاعبون بالإرادة الحرة في البطاقة الثالثة، ولكن بوند يشير بالفعل إلى اللعبة لفظيًا باسم "chemin de fer" في النقطة 2:11 في الفيديو:
يُظهر الفيديو التالي ثلاثة مشاهد من لعبة chemin de fer من ثلاثة أفلام مختلفة.
وهنا نقاط البداية لكل مشهد:
- 2:09 — كرة الرعد
- 4:19 — حول الخدمة السرية لجلالة الملكة
- 7:30 — لعينيك فقط
في كل هذه الألعاب نرى اللاعبين يعتمدون على البنوك ويختارون بحرية في قرار البطاقة الثالثة، وخاصة في لعبة For Your Eyes Only، حيث تتم مناقشة الاحتمالات.
وأخيرًا، أدناه المشهد من فيلم Goldeneye.
هنا نرى مجددًا تناوب الرهان على البنك، والاختيار الحر في سحب البطاقة الثالثة. مع ذلك، تُشير الشخصية الأنثوية إلى اللعبة باسم "باكارات" عند الدقيقة 0:45. أنصح بتصنيف هذا تحت "خطأ في الشخصية".
في الختام، لا شك أن بوند كان يلعب لعبة "الشمان دو فير" في كل فيلم. من الناحية الفنية، أعتقد أن الحكام أخطأوا في قبول "الباكارات" كإجابة صحيحة. مع ذلك، لا ألومهم. حتى بمعايير برنامج "جيوباردي"، فإن توقع معرفة اللاعب العادي للباكارات من لعبة "الشمان دو فير" أمرٌ مُبالغ فيه. وكما يتضح من قبول إجابة "الموتش" بدلاً من أنتوني سكاراموتشي، فإنهم يزدادون تساهلاً.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
كما سئل في فيلم Mean Girls ، ما هو:
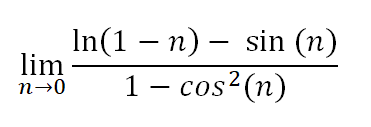
لنبدأ بالنظر إلى رسم بياني لـ n (محور x) وf(n) (محور y).
كما ترى، يقترب الحد من ∞ من اليسار و-∞ من اليمين. ولأنه لا ينعكس إلى نفس المكان من كلا الجانبين، فلا يوجد حد.
مع ذلك، لنُجِب على السؤال دون تمثيل بياني. تنص قاعدة لوبيتال على أنه إذا كانت نهاية f(x)/g(x) = 0/0، فإن lim f(x)/g(x) = lim f'(x)/g'(x). لذا، لنُحَل قيم f'(x) وg'(x).
f'(n) = ((ln(1-n) - sin(n)) d/dn = -1/(1-n) - cos(n)
g'(n) = (1 - cos 2 (n)) d/dn = sin 2 (n) d/dn
دعنا نستخدم قاعدة الضرب لحل sin 2 (n) d/dn
الخطيئة 2 (ن) د/دن = الخطيئة(ن) × الخطيئة(ن) د/دن =
الخطيئة (ن) × جتا (ن) + جتا (ن) × الخطيئة (ن) =
2sin(n)cos(n).
الآن، دعنا نحل f'(n) و g'(n) عند n = 0.
f'(0) = -1/(1-0) - cos(0) = -2.
g'(0) = 2sin(0)cos(0) = 0
إذًا، f'(0)/g'(0) = -2/0 = -∞. وبالتالي، فإن نهاية الدالة الأصلية غير موجودة.
أود أن أشيد بكتاب فيلم "فتيات لئيمات" على دقة حساباتهم. حتى الأفلام الرياضية الجادة، مثل "غود ويل هانتينغ"، غالبًا ما تُخفق في تطبيقها.