WOO logo

يوصي المعالج

اسأل الساحر #422

جدليًا، بافتراض وجود عدد لا نهائي من مجموعات أوراق البلاك جاك، يُسمح بإعادة تقسيم الأوراق لعدد لا نهائي، وسيقسم اللاعب أي زوج. ما هو احتمال أي عدد معين من الأيدي النهائية التي يلعبها اللاعب؟

مجهول

احتمال إعادة التقسيم إلى n يد هو (combin(2*(n-1),n-1)/n) × (1/13)^(n-1) × (12/13)^n. لمزيد من المعلومات حول هذا المصطلح الأول، والذي احتجتُ إلى بعض المساعدة فيه، ابحث عن الأعداد الكاتالونية .

يوضح الجدول التالي احتمالية ظهور يد نهائية من ١ إلى ٢٠ يدًا. عمود الثواني هو عدد "الأشجار"، وهو الرقم الكاتالوني في العبارة أعلاه.

اليدين الأشجار احتمال
1 1 0.9230769230769
2 1 0.0655439235321
3 2 0.0093080128093
4 5 0.0016523099661
5 14 0.0003285065968
6 42 0.0000699777366
7 132 0.0000156163334
8 429 0.0000036037693
9 1430 0.0000008529631
10 4862 0.0000002059225
11 16796 0.0000000505114
12 58786 0.0000000125531
13 208012 0.0000000031540
14 742900 0.0000000007998
15 2674440 0.0000000002045
16 9694845 0.0000000000526
17 35357670 0.0000000000136
18 129644790 0.0000000000035
19 477638700 0.0000000000009
20 1767263190 0.0000000000002

سمعتُ أن هناك عددًا لا نهائيًا من ثلاثيات فيثاغورس. هل من طريقة صيغية لإيجادها؟

مجهول

نعم، هناك عدد لا نهائي من ثلاثيات فيثاغورس الفريدة! لمن لا يعرف هذا المصطلح، فهي مثلثات قائمة حيث يكون كل ضلع فيها عددًا صحيحًا. أشهرها هو 3-4-5. للحصول على مجموعة فريدة (أي غير قابلة للاختزال)، اختر أي قيمة صحيحة لثلاثية فيثاغورس a وb، حيث a < b، وواحد منها فردي والآخر زوجي.

  • الساق 1 = ب 2 - أ 2
  • الساق 2 = 2ab
  • الوتر = أ 2 + ب 2

يوضح الجدول التالي جميع الثلاثيات فيثاغورس غير القابلة للاختزال حيث تكون جميع الأضلاع 101 أو أقل.

أ،ب المرحلة 1 المرحلة الثانية وتر
1,2 3 4 5
1,4 8 15 17
1,6 12 35 37
1,8 16 63 65
1,10 20 99 101
2,3 5 12 13
2,5 20 21 29
2,7 28 45 53
2,9 36 77 85
3,4 7 24 25
3,6 27 36 45
3,8 48 55 73
4,5 9 40 41
4,7 33 56 65
4,9 65 72 97
5,6 11 60 61
5,8 39 80 89
6,7 13 84 85

ما هو احتمال الحصول على مجموع كلي، باستخدام نردين، غير السبعة، مرتين على الأقل، قبل الحصول على سبعة؟

Garrison

الحيلة في أسئلة مثل هذا هي أن الاحتمال هو نفسه إذا كان الوقت بين اللفات يتبع توزيعًا أسيًا بمتوسط 1. في هذه الحالة، يمكن إعطاؤه بالصيغة التالية.

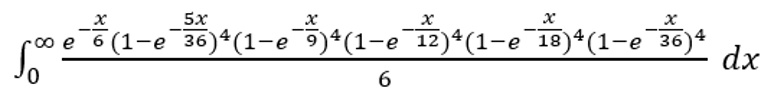
لوضعها في شكل نص: exp(-x/6)*(1-exp(-5x/36))^4*(1-exp(-4x/36))^4*(1-exp(-3x/36))^4*(1-exp(-2x/36))^4*(1-exp(-1x/36))^4/6

لحل مثل هذه التكاملات، أوصي باستخدام حاسبة التكامل هذه.

الجواب هو 7864581698887803455719/10946915593544650625105200 =~ 0.0007184290069364848.