ألعاب غير كازينو - التعليمات
أحب لعب بوكر الكاذبين بأوراق الدولار. ما احتمال ظهور أي رقم من نفس النوع على ورقة نقدية؟ شكرًا لك. إذا كنت ألعب مع ثلاثة أشخاص، فما احتمال ظهور أي رقم واحد؟
دعوني أولاً أجيب على السؤال غير المطروح حول احتمال ظهور رقم معين n مرة على ورقة نقدية عشوائية. تحتوي الورقة النقدية على 8 أرقام، لذا فإن احتمال ظهور رقم معين n هو: combin(8,n)*0.1 n *0.9 8-n /10 8. إليكم جدولًا يوضح احتمال ظهور رقم معين من 0 إلى 8.
احتمالات رقم محدد في لعبة البوكر الكاذبة
| رقم | احتمال |
|---|---|
| 8 | 0.00000001 |
| 7 | 0.00000072 |
| 6 | 0.00002268 |
| 5 | 0.00040824 |
| 4 | 0.00459270 |
| 3 | 0.03306744 |
| 2 | 0.14880348 |
| 1 | 0.38263752 |
| 0 | 0.43046721 |
| المجموع | 1.00000000 |
يوضح الجدول التالي احتمالية كل نوع ممكن من الأوراق النقدية، مُصنّفًا حسب عدد كل ن من نفس النوع. على سبيل المثال، الرقم التسلسلي 66847680 سيحتوي على ثلاثة أنواع، وزوج واحد، وثلاثة أنواع مفردة، باحتمالية 0.1693440.
الاحتمالات العامة في لعبة البوكر الكاذب
| 8 بلوط | 7 بلوط | 6 بلوط | 5 بلوط | 4 بلوط | 3 بلوط | 2 بلوط | 1 بلوط | احتمال |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.0000001 | |||||||
| 1 | 1 | 0.0000072 | ||||||
| 1 | 1 | 0.0000252 | ||||||
| 1 | 2 | 0.0002016 | ||||||
| 1 | 1 | 0.0000504 | ||||||
| 1 | 1 | 1 | 0.0012096 | |||||
| 1 | 3 | 0.0028224 | ||||||
| 2 | 0.0000315 | |||||||
| 1 | 1 | 1 | 0.0020160 | |||||
| 1 | 2 | 0.0015120 | ||||||
| 1 | 1 | 2 | 0.0211680 | |||||
| 1 | 4 | 0.0211680 | ||||||
| 2 | 1 | 0.0020160 | ||||||
| 2 | 2 | 0.0141120 | ||||||
| 1 | 2 | 1 | 0.0423360 | |||||
| 1 | 1 | 3 | 0.1693440 | |||||
| 1 | 5 | 0.0846720 | ||||||
| 4 | 0.0052920 | |||||||
| 3 | 2 | 0.1270080 | ||||||
| 2 | 4 | 0.3175200 | ||||||
| 1 | 6 | 0.1693440 | ||||||
| 8 | 0.0181440 | |||||||
| المجموع | 1.0000000 | |||||||
البلوط = "من نوع ما"
لمزيد من المعلومات، راجع صفحتي على liars poker .
يقدم بنك أوف أمريكا عرضًا لمضاعفة إيداع محدد يوميًا في أجهزة الصراف الآلي بثلاثة أضعاف. تستمر المسابقة لمدة شهرين تقريبًا. هل فرصي أفضل عند إيداع 300 دولار... لإجراء ثلاث إيداعات بقيمة 100 دولار أو إيداع واحد بقيمة 300 دولار... أم أن فرصي الإجمالية منخفضة جدًا بحيث لا يستحق العناء؟
ربحك المتوقع ثابت بغض النظر عن عدد مرات تقسيم إيداعاتك. الاستراتيجية الجيدة هي إيداع وسحب نفس المبلغ مرارًا وتكرارًا قدر الإمكان. مع ذلك، قد تكون فرصك ضئيلة جدًا بحيث لا يستحق الأمر كل هذا العناء.
سؤال حول لعبة نرد شرقية، حيث يُفترض باللاعبين تخمين أي وجه من وجوه النرد سيظهر. يضع اللاعبون رهاناتهم أولاً على الأرقام 1، 2، 3، 4، 5، 6 (كما في الروليت)، ثم يقوم الموزع برمي 3 نرد في آنٍ واحد. تكون نسبة العائد 1:1 إذا ظهرت الأرقام المختارة مرة واحدة (على أيٍّ من النردات الثلاثة)، و2:1 إذا ظهر الرقم "لا" مرتين، و3:1 إذا ظهر الرقم المختار على جميع النردات الثلاثة. بما أن اللاعب يستطيع وضع أي عدد من الرهانات على اللوحة، فما هو العدد الأمثل للرهانات؟ (بافتراض أن جميع رهاناتي متساوية في الحجم)
احتمال مطابقة ثلاثة أرقام هو ١/٢١٦. احتمال مطابقتين هو ٣*٥/٢١٦. احتمال مطابقة واحدة هو ٢٥*٥/٢١٦. احتمال عدم مطابقة أي رقم هو ٥*٥*٥/٢١٦. لذا، فإن العائد المتوقع هو ٣*(١/٢١٦)+٢*(١٥/٢١٦)+١*(٧٥/٢١٦)-١*(١٢٥/٢١٦)=-١٧/٢١٦=-٧.٨٧٪. لا يوجد عدد مثالي للرهانات، وستخسر ٧.٨٧٪ من إجمالي قيمة الرهان مهما فعلت.
يمكن إجراء هذه الرهانات في كل من لعبة sic bo ولعبة chuck a luck .
ما هي احتمالات الفوز في لعبة Klondike Solitaire القياسية كما في إصدار Windows؟
ربما يكون هذا هو السؤال الأكثر شيوعًا الذي أتلقاه والذي لا أملك إجابة عليه. لم يسبق لأحد أن لعب لعبة سوليتير كلوندايك كاملة. ربما، عندما تصبح أجهزة الكمبيوتر أسرع بملايين المرات، سيفعلها أحدهم في النهاية. مع ذلك، يُشاع أن كازينوهات فيغاس كانت تُقدم اللعبة منذ خمسينيات القرن الماضي على الأقل. لقد طلبت من عدد من مُحبي فيغاس القدامى التحقق من ذلك، لكن لم يتمكن أي منهم من ذلك حتى الآن.
لقد رميتُ مؤخرًا، خلال لعبة طاولة زهر، رقمًا مزدوجًا ستة أربع مرات متتالية. ما احتمالات تكرار ذلك؟
مع كل لفة جديدة، احتمال أن تكون اللفات الأربع التالية كلها ستة مزدوجة هو (1/36) 4 = 1 في 1679616.
مرحباً، على موقع www.transience.com.au/pearl.html ، توجد لعبة تُسمى "لآلئ الخنازير". اللآلئ مُجمّعة في ثلاثة صفوف (5 + 4 + 3)، وفي دورك، يمكنك إزالة أي عدد تريده من اللآلئ من صف واحد. هدف اللعبة هو ترك آخر اللآلئ لخصمك ليأخذها. اللاعب (أنا) هو من يبدأ اللعبة دائماً (ويخسر دائماً). لماذا لا أفوز أبداً؟ لدى خصمي نظام ذكي للفوز دائماً، هل يمكنك كشف سره؟
ابدأ بإزالة لؤلؤتين من الصف الذي يحتوي على 3 لؤلؤات، ليتبقى 1+4+5. بغض النظر عما يفعله خصمك في دورك التالي، اتركه مع أيٍّ من الخيارات التالية: 1+1+1، 1+2+3، أو 4+4. من أيٍّ من هذه الخيارات، اجبر خصمك على وضع كومتين من لؤلؤتين أو أكثر، أو عدد فردي من الأكوام من لؤلؤة واحدة.
ما هي أفضل مجموعة في لعبة المونوبولي؟
أفضل المجموعة البرتقالية، فهي توفر أفضل عائد استثمار. على سبيل المثال، يبلغ سعر الفندق ٥٠٠ دولار للمجموعة البرتقالية، ومتوسط إيجاره ٩٦٦.٦٧ دولارًا، بنسبة إيجار إلى مصاريف ١.٩٣. المجموعة الوحيدة ذات النسبة الأعلى هي المجموعة الزرقاء الفاتحة، بنسبة ٢.٢٧. مع ذلك، يبلغ الحد الأقصى للإيجار للمجموعة الزرقاء الفاتحة ٦٠٠ دولار فقط. إيجارات المنازل المكونة من ثلاثة منازل في المجموعة البرتقالية مماثلة لإيجارات الفنادق في المجموعة الزرقاء الفاتحة، ولكنها أقل بنسبة ٢٠٪، مع وجود مساحة لبناء المزيد. كما أن المجموعة البرتقالية جاهزة للسكن فور خروجك من السجن. لذا، اتبع نصيحتي، وحاول عند التداول الحصول على المجموعة البرتقالية.
ما هي نصيحتك للعبة الحجارة/الورقة/المقص؟
أفضل نصيحة في هذا الموقع قد تكون: في الجولة الأولى، اختر الورقة دائمًا. وذلك لأن اللاعبين الهواة يميلون إلى اختيار الحجر من المرة الأولى. ما عليك سوى مد يدك في كل موضع، واحدًا تلو الآخر، وستجد أن الحجر هو الخيار الأكثر راحة وطبيعية. إذا لعبت جولات متكررة، فيجب عليك اختيار ما يهزم خصمك في الجولة الأخيرة باحتمالية أقل من الثلث. وذلك لأنني أعتقد أن الهواة يكررون أقل من ثلث الوقت. إذا كنت تلعب مع لاعب محترف تخشى أن يتسلل إلى رأسك، فقم بالاختيار العشوائي من خلال النظر إلى عقرب الثواني في ساعتك، واقسم عدد الثواني على ثلاثة وخذ الباقي، ثم قم بربط الباقي على النحو التالي: 0 = حجر، 1 = مقص، 2 = ورقة (أو أي ربط آخر طالما تم تحديده مسبقًا). لذا في المرة القادمة التي تذهب فيها إلى مطعم على الطريقة الهولندية، أقترح عليك لعب جولة واحدة للفحص ثم اختر الورقة. يمكنك أن تشكرني لاحقًا.
من لديه الأفضلية في لعبة Risk عندما يقوم المهاجم برمي ثلاثة نرد ويقوم المدافع برمي نردين؟
لمن لا يعرف لعبة "ريسك"، فهي أعظم لعبة لوحية على الإطلاق. من لم يلعبها لم يعشها بعد. للإجابة على سؤالك في معركة 3 ضد 2 الشائعة، إليك النتائج المحتملة:
- المدافع يخسر كلاهما: 37.17%
- كل واحد يخسر واحد: 33.58%
- يخسر المهاجم كلاهما: 29.26%
في لعبة الياتزي، إذا بقيت فقط بطاقة الياتزي نفسها على البطاقة، ما هو احتمال الحصول عليها؟
يوضح الجدول التالي احتمال النجاح في اللفة الأخيرة وفقًا لعدد النرد الإضافي الذي تحتاجه لصنع Yahtzee.
احتمالات لعبة ياهتزيز في آخر لفة
| ضروري | احتمال من النجاح |
| 0 | 1 |
| 1 | 0.166667 |
| 2 | 0.027778 |
| 3 | 0.00463 |
| 4 | 0.000772 |
يوضح الجدول التالي احتمالات التحسن. يوضح العمود الأيسر عدد النرد اللازم قبل أي رمية، بينما يوضح العمود العلوي العدد اللازم بعد الرمية. يوضح الجدول احتمالية درجة التحسن المحددة.
احتمالات التحسين
| الحاجة قبل اللفة | 0 | 1 | 2 | 3 | 4 | المجموع |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0.166667 | 0.833333 | 0 | 0 | 0 | 1 |
| 2 | 0.027778 | 0.277778 | 0.694444 | 0 | 0 | 1 |
| 3 | 0.00463 | 0.069444 | 0.37037 | 0.555556 | 0 | 1 |
| 4 | 0.000772 | 0.01929 | 0.192901 | 0.694444 | 0.092593 | 1 |
الجدول التالي يوضح احتمالية الحاجة إلى 0 إلى 4 أحجار نرد إضافية في اللفة الأولية لتكوين Yahtzee.
احتمالات لعبة ياهتزيه في اللفة الأولى
| ضروري | احتمال |
| 0 | 0.000772 |
| 1 | 0.019290 |
| 2 | 0.192901 |
| 3 | 0.694444 |
| 4 | 0.092593 |
يوضح الجدول التالي احتمالية التحسن، ثم النجاح النهائي، وفقًا للعدد المطلوب بعد الرمية الأولى. على سبيل المثال، إذا احتاج اللاعب إلى 3 أحجار نرد إضافية لتشكيل ياتزي، فإن احتمالية التحسن إلى الحاجة إلى حجرين إضافيين بعد الرمية الثانية والفوز بالياتزي في الرمية الثالثة هي 0.010288066.
احتمالات لعبة ياتزي بعد اللفة الأولى وفقًا للعدد المطلوب قبل وبعد اللفة الثانية
| الحاجة قبل اللفة | 0 | 1 | 2 | 3 | 4 | المجموع |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0.166667 | 0.138889 | 0 | 0 | 0 | 0.305556 |
| 2 | 0.027778 | 0.046296 | 0.01929 | 0 | 0 | 0.093364 |
| 3 | 0.00463 | 0.011574 | 0.010288 | 0.002572 | 0 | 0.029064 |
| 4 | 0.000772 | 0.003215 | 0.005358 | 0.003215 | 0.000071 | 0.012631 |
للحصول على الإجابة النهائية، احسب حاصل الضرب النقطي للعدد المطلوب بعد رمية النرد الأولى على طاولتين، ثم احسب احتمالية النجاح في العمود الأخير على طاولة واحدة. هذا يساوي 0.092593*0.012631+ 0.694444*0.029064 + 0.192901*0.093364 + 0.019290*0.305556 + 0.000772*1 = 4.6028643%. للتأكد من ذلك، أجريت محاكاة للعبة 100,000,000، وكانت احتمالية المحاكاة 4.60562%.
إذا تم تقديم الديناميت كخيار في لعبة الحجر والورق والمقص، حيث يتغلب الديناميت على الحجر والورق، ولكن المقص يتغلب على الديناميت، فما هي الاستراتيجية المثالية التي يجب اتباعها إذا كان هناك منطقيان مثاليان يلعبان؟
أولاً، يمكننا استبعاد فكرة لعب الورق. بغض النظر عمّا يرميه اللاعب الآخر، ستُحقق نتيجة مساوية أو أفضل برمي الديناميت على الورقة. بمجرد استبعاد الورقة، يصبح الديناميت هو الورقة الجديدة، متغلبًا على الحجرة ومُخسرًا أمام المقص. لذا، فإن الاستراتيجية المثالية هي الاختيار عشوائيًا، وباحتمالات متساوية، بين الحجرة والمقص والديناميت.
ما هي أفضل استراتيجية في أحد تلك الأكشاك مع الأموال التي تطير في كل مكان بينما يتعين عليك جمع أكبر قدر ممكن في فترة زمنية محدودة؟
طرحتُ هذا السؤال على راندي هيل من شركة "فن إندستريز" . قال إنه يجب عليك مد ذراعيك، وراحة يديك للأسفل، وترك النقود تتدفق على باطن يديك وذراعيك. عندما يتراكم لديك ما يكفي، ضعها في الفتحة.
لنفترض أن لدينا لعبة قمار. عُرضت عملة معدنية غير متحيزة بشكل متكرر. في كل رمية، علينا دفع روبية واحدة. هناك نتيجتان محتملتان: H أو T. إذا أصبح الفرق بين رمية الرأس ورمية الكتابة 3، فسنحصل على 8 روبيات من المقامر. هل يجب أن نلعب اللعبة، ولماذا؟ ما هو احتمال فوزنا؟ ما الذي يجب أن يؤثر على احتمال الفوز عندما نحصل على 7 أو 9 روبيات؟
دعونا نطلق على x عدد التقلبات المتوقعة من نقطة البداية.
دعونا نسمي y عدد التقلبات المتبقية المتوقعة إذا كان أحد الجانبين هو تقلب واحد في الأغلبية.
دعونا نطلق على z العدد المتوقع للتقلبات المتبقية إذا كان أحد الجانبين يحتوي على تقلبين في الأغلبية.
E(x) = 1 + E(y)
E(y) = 1 + 0.5*E(x) + 0.5*E(z)
E(z) = 1 + 0.5*E(y)
من السهل إذن، من خلال جبر المصفوفات، أن نلاحظ أن E(x) = 9، وE(y) = 8، وE(z) = 5. لذا، في المتوسط، سيستغرق الأمر 9 رميات ليصبح الفرق بين النقش والكتابة 3. لذا، عند 8 روبيات، يُعد هذا رهانًا جيدًا لمن يحصل على روبية واحدة في كل رمية، لأنه سيحصل في المتوسط على 9 روبيات، لكنه سيسدد 8 روبيات فقط. تبلغ نسبة ربح الكازينو للمقامر 11.11%. عند 9 روبيات، يُعد رهانًا عادلًا، أما عند 7 روبيات، فتبلغ نسبة ربح الكازينو 22.22%.
في مقالك بتاريخ ٢٨ نوفمبر ٢٠٠٢، تناولتَ الاستراتيجية المناسبة للعبة "لآلئ قبل الخنازير" . هناك أيضًا جزء ثانٍ بعنوان "لآلئ قبل الخنازير ٢" . كيف يُمكنني الفوز بهذه النسخة؟
أشرح في عمود ٢٨/١١/٢٠٠٢ كيفية اللعب عندما يتبقى ثلاثة صفوف فقط. إليك استراتيجيتي للعب بأربعة صفوف. عندما يحين دورك، انظر إلى ترتيب الصفوف على طول العمود الأيسر والعب ما هو موجود في العمود الأيمن. على سبيل المثال، موضع البداية ٣٤٥٦ هو الأخير، ويُظهر أنه يجب عليك إزالة ٤ لآلئ من الصف الذي يحتوي على ٥، ليتبقى ١٣٤٦. إذا كان العمود الأيسر يقول "خسارة"، فلا سبيل للفوز إذا اتبع الخصم الاستراتيجية المثلى، وهو ما يبدو أن لعبة Transcience تفعله دائمًا.
يبدو أن أحد أنماط هذا الجدول هو إجبار الخصم على وضع يكون فيه مجموع اللآلئ في أصغر وأكبر الصفوف مساويًا لمجموع اللآلئ في المنتصف. وهذا يشمل ترك صفر في الصف الذي يحتوي على أقل عدد من اللآلئ.
استراتيجية لآلئ قبل الخنازير الجزء الثاني
| لديك | يترك |
| 1111 | 111 |
| 1112 | 111 |
| 1113 | 111 |
| 1114 | 111 |
| 1115 | 111 |
| 1116 | 111 |
| 1122 | يخسر |
| 1123 | 1122 |
| 1124 | 1122 |
| 1125 | 1122 |
| 1126 | 1122 |
| 1133 | يخسر |
| 1134 | 1133 |
| 1135 | 1133 |
| 1136 | 1133 |
| 1144 | يخسر |
| 1145 | 1144 |
| 1146 | 1144 |
| 1155 | يخسر |
| 1156 | 1155 |
| 1222 | 1122 |
| 1223 | 1122 |
| 1224 | 1122 |
| 1225 | 1122 |
| 1226 | 1122 |
| 1233 | 123 |
| 1234 | 123 |
| 1235 | 123 |
| 1236 | 123 |
| 1244 | 1144 |
| 1245 | 145 |
| 1246 | 246 |
| 1255 | 1155 |
| 1256 | يخسر |
| 1333 | 1133 |
| 1334 | 1133 |
| 1335 | 1133 |
| 1336 | 1133 |
| 1344 | 1144 |
| 1345 | 145 |
| 1346 | يخسر |
| 1355 | 1155 |
| 1356 | 1256 |
| 1444 | 1144 |
| 1445 | 1144 |
| 1446 | 1144 |
| 1455 | 1155 |
| 1456 | 1346 |
| 2222 | يخسر |
| 2223 | 2222 |
| 2224 | 2222 |
| 2225 | 2222 |
| 2226 | 2222 |
| 2233 | يخسر |
| 2234 | 2233 |
| 2235 | 2233 |
| 2236 | 2233 |
| 2244 | يخسر |
| 2245 | 2244 |
| 2246 | 2244 |
| 2255 | يخسر |
| 2256 | 2255 |
| 2333 | 2233 |
| 2334 | 2233 |
| 2335 | 2233 |
| 2336 | 2233 |
| 2344 | 2244 |
| 2345 | يخسر |
| 2346 | 1346 |
| 2355 | 2255 |
| 2356 | 2345 |
| 2444 | 2244 |
| 2445 | 2244 |
| 2446 | 2244 |
| 2455 | 2255 |
| 2456 | 2345 |
| 3333 | يخسر |
| 3334 | 3333 |
| 3335 | 3333 |
| 3335 | 3333 |
| 3336 | 3333 |
| 3344 | يخسر |
| 3345 | 3344 |
| 3346 | 3344 |
| 3355 | يخسر |
| 3356 | 3355 |
| 3444 | 3344 |
| 3445 | 3344 |
| 3446 | 3344 |
| 3455 | 3355 |
| 3456 | 1346 |
كتب براد س. ليضيف استراتيجية عامة لأي عدد من اللآلئ والصفوف. أولًا، عليك تقسيم كل صف إلى مكوناته الثنائية. على سبيل المثال، نقطة بداية لعبة Transcience ستكون كما يلي.
- 3 = 2 + 1
- 4 = 4
- 5 = 4 + 1
- 6 = 4 + 2
ثم حاول ترك عدد زوجي من كل قوة من قوى 2. على سبيل المثال، في المثال السابق، يوجد رقمان 1، ورقمان 2، وثلاثة أرقام 4. وبالتالي، يصبح لديك 4 إضافية. ثم احذف 4 من أي صف يحتوي على حد 4. استمر في ذلك حتى تتمكن من تقليص عدد أرقام خصمك إلى 2، أو 2، أو عدد فردي من الأرقام 1.
جرب هذه الاستراتيجية في لعبة بيرل 3 ، ستفوز دائمًا. إذا بدأتَ بخسارة كما فعلتُ في اللعبة 10 (4+7+8+11)، يمكنك الضغط على "انطلق" لجعله يبدأ أولًا.
أنا لا أفهم لعبة نيم الخاصة بك! لطالما اعتقدت أن مفتاح الفوز هو ترك خصمك (في هذه الحالة، الحاسوب) مع نقاط مجموعها يساوي العدد الأدنى التالي الذي يساوي مجموعها بالأرقام الثنائية، أي إذا كان لديّ 17 نقطة، فسأأخذ 2 وأترك 15، أي مجموع الأرقام الثنائية 1، 2، 4، 8. لكن يبدو أن هذا لا ينجح. هل أنا على صواب أم خطأ؟
أنت على الطريق الصحيح مع الأرقام الثنائية، ولكن هذه ليست استراتيجية الفوز تمامًا. أولًا، إذا استطعت ترك خصمك بعدد فردي من الصفوف، كل صف يحتوي على رقم واحد، فافعل ذلك. وإلا، فقسّم كل صف إلى مكوناته الثنائية. على سبيل المثال، 99 يساوي 64 + 32 + 2 + 1. ثم اجمع عدد كل مكون على جميع الصفوف. ثم ابحث عن طريقة تجعل خصمك يمتلك عددًا زوجيًا من جميع المكونات الثنائية على جميع الصفوف.
لنلقِ نظرة على مثال. لنفترض أن دورك في السيناريو التالي.
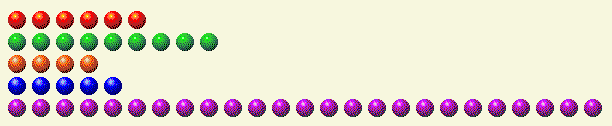
يقوم الجدول التالي بتقسيم كل صف إلى مكوناته الثنائية.
دور اللاعب 1
| صف | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 25 | 1 | 0 | 0 | 1 | 1 |
| المجموع | 3 | 1 | 3 | 2 | 1 |
كما ترى، هناك عدد فردي من الآحاد والاثنينات والأربعات والستة عشر. من الواضح أننا نحتاج إلى وضع صف الـ ٢٥ تحت ١٦ لحذف الوحدة ١٦. وللحفاظ على مجموع العناصر الثنائية زوجيًا، نحتاج إلى حذف ١، وإضافة ٢، وإضافة ٤، والإبقاء على ٨، ثم حذف ١٦. هذا يعني أن أفضل طريقة هي ٢ + ٤ + ٨ = ١٤ في الصف الأخير. وبترك ١٤ في الصف السفلي، نحصل على ما يلي.
دور الكمبيوتر 1
| صف | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 14 | 0 | 1 | 1 | 1 | 0 |
| المجموع | 2 | 2 | 4 | 2 | 0 |
يأتي دور الكمبيوتر، ويترك لنا هذا.
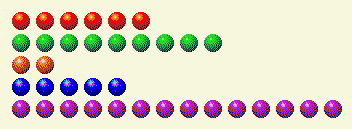
وهنا التقسيم الثنائي لذلك.
دور اللاعب الثاني
| صف | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 14 | 0 | 1 | 1 | 1 | 0 |
| المجموع | 2 | 3 | 3 | 2 | 0 |
هنا نحتاج إلى حذف ٢ و٤ لنحصل على المجموعين متساويين. يوجد صف واحد فقط، وهو الصف ١٤، والذي يحتوي على كلا العنصرين. لذا، نحذف ٦ منه، ليتبقى ٨.
دور الكمبيوتر الثاني
| صف | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 0 |
| المجموع | 2 | 2 | 2 | 2 | 0 |
يأتي دور الكمبيوتر، ويترك لنا هذا.
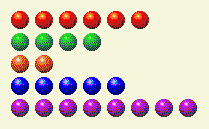
الآن نحتاج إلى تغيير الأعمدة 1 و 4 و 8.
دور اللاعب الثالث
| صف | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 0 |
| المجموع | 1 | 2 | 3 | 1 | 0 |
يمكن القيام بذلك عن طريق تغيير الصف من 8 إلى 5 على النحو التالي.
دور الكمبيوتر الثالث
| صف | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| المجموع | 2 | 2 | 4 | 0 | 0 |
يأتي دور الكمبيوتر، ويترك لنا هذا.
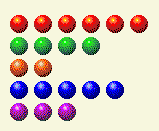
الآن نحتاج إلى تغيير الإجمالي 2 و 4.
دور اللاعب الرابع
| صف | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| المجموع | 2 | 3 | 3 | 0 | 0 |
يمكن القيام بذلك عن طريق تغيير الرقم 6 إلى 0.
دور الكمبيوتر الرابع
| صف | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| المجموع | 2 | 2 | 2 | 0 | 0 |
يأتي دور الكمبيوتر، ويترك لنا هذا.
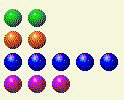
الآن نحتاج إلى تغيير 2 و 4.
دور اللاعب الخامس
| صف | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| المجموع | 2 | 3 | 1 | 0 | 0 |
يمكن تحقيق ذلك عن طريق تغيير الصف من 5 إلى 3. إذا تمكنت يومًا ما من جعل خصمك يصل إلى موقف x،x،y،y، فلن يمكنك إلا الفوز، إذا تمكنت من الحفاظ على نفس الموقف حتى النهاية.
دور الكمبيوتر الخامس
| صف | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| المجموع | 2 | 4 | 0 | 0 | 0 |
في الحركات القليلة التالية، أبقي الحاسوب على أنماط س، س، ص، ص. هنا يتركني الحاسوب مع ٢، ٢، ٣، ٢؛ لذا أتركه مع ٢، ٢، ٢، ٢.

ثم يُعطيني الحاسوب ٢، ٢، ١، ٢. فأتركه مع ٢، ٢، ١، ١.
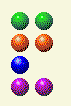
ثم يتركني الحاسوب مع ٢، ٢، ١. فأتركه مع ٢، ٢. إذا استطعتَ يومًا ما أن تجعل خصمك يصل إلى صفين متساويين، فلا مفر من الفوز، فقط حافظ على تساوي الصفين.

ثم يتركني الكمبيوتر مع كومة واحدة من 2، وأقوم بإزالة 1.

وهنا نهاية اللعبة.
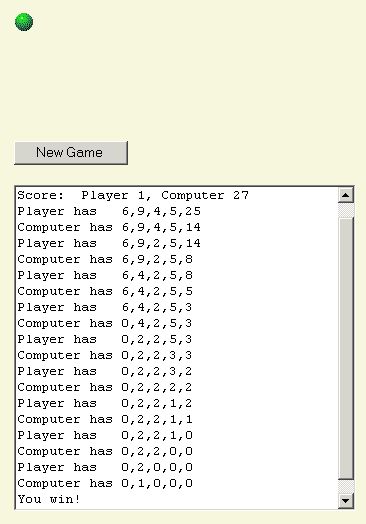
اشتريتُ مؤخرًا عجلة كرنفال كانت ملكًا لعمي الأكبر، عمرها حوالي مئة عام، وأحاول تطوير لعبة حولها. مرقمة من ١ إلى ٦٠ عشوائيًا، وتتناوب بين الأسود والأحمر مع نجمة خضراء كل خمسة عشر. هل يمكنك مساعدتي في تحديد قيمة المكافآت لكل دورة؟
إذن، لدينا 30 رقمًا أسود، و30 رقمًا أحمر، و4 أرقام خضراء. هذا يعني أن احتمالية اللون الأسود هي 30/64، والأحمر 30/64، والأخضر 4/64. إذا كان احتمال وقوع حدث ما هو p، فإن الاحتمالات العادلة هي (1-p)/p إلى 1. لذا، فإن الاحتمالات العادلة لأي لون أحمر هي (34/64)/(30/64) = 34 إلى 30 = 17 إلى 15. وينطبق الأمر نفسه على اللون الأسود. والاحتمالات العادلة للون الأخضر هي (60/64)/(4/64) = 60 إلى 4 = 15 إلى 1. وبالنسبة لرقم محدد، فإن الاحتمالات العادلة هي (63/64)/(1/64) إلى 63 إلى 1.
أقترح دفع 1 إلى 1 على الأحمر والأسود، و14 إلى 1 على الأخضر، و60 إلى 1 على أي رقم فردي. إحدى صيغ نسبة ربح الكازينو هي (ta)/(t+1)، حيث t هي الاحتمالات الحقيقية، وa هي الاحتمالات الفعلية. في هذه الحالة، تكون نسبة ربح الكازينو على رهان الأحمر أو الأسود (63-60)/(63+1) = 3/64 = 4.69%. أما على رهان الأخضر، فتبلغ نسبة ربح الكازينو (15-14)/(15+1) = 1/16 = 6.25%. أما على الأرقام الفردية، فتبلغ نسبة ربح الكازينو (63-60)/(63+1) = 3/64 = 4.69%.
في ولاية نيويورك، توجد أجهزة يانصيب فيديو (VLT) في أماكن المراهنات خارج المضمار. تسمع عبارة "تقترب الآلة من نقطة الضبط" عندما تصبح آلة VP "ساخنة" وتوزع يدًا رابحة تلو الأخرى. هذا يفسر سبب قيام نفس الآلة بالدفع في يوم ما وعدم رغبتها في معرفة رصيدك في أيام أخرى. كما أن معظم هذه الآلات لا تسمح لك بخسارة يد رابحة. تخلص منها وستُعيد لك يدًا مساوية أو أفضل. ما رأيك في هذا الموضوع؟
ألعاب VLT هي ألعاب سحب ألسنة مُمجدّة. هناك مجموعة نتائج مُحددة مُسبقًا. عند اللعب، تختار اللعبة نتيجة عشوائية من المجموعة، وتعرض الفوز للاعب على شكل ماكينة قمار أو لعبة فيديو بوكر. ولأن النتيجة مُقدّرة مُسبقًا، فإن أي عنصر من عناصر المهارة يكون خياليًا. على سبيل المثال، إذا قُدّمت لك مجموعة رويال فلاش ورميتها بعيدًا، فستحصل على واحدة أخرى عند السحب. عادةً ما أقول إنه في المقامرة، لا يُهم الماضي، ولكن في هذه الحالة، هناك تأثير الإزالة. إذا لعبت مرة واحدة وخسرت، فسيُحسّن ذلك بشكل طفيف احتمالات نتائج اللعبة المتبقية، حتى ينفد مخزون مجموعات السحب الافتراضية، وأفترض أن الطبلة الافتراضية تُملأ مُجددًا. أعتقد أن تقلباتك المُتذبذبة هي مجرد حظ طبيعي، وأي قدر مُسبق هو من نسج الخيال.
أضاف أحد القراء فيما بعد ما يلي إلى هذا الموضوع.
لديّ تعليق على مقالتك "اسأل الساحر" المنشورة في ١٤ فبراير (العدد ١٨٣). لا علاقة له بالسؤال الذي أجبتَ عنه، بل هو مجرد شيء قد يثير اهتمامك.
قبل إقرار الاقتراح 1A، الذي سمح بإقامة ألعاب كاملة من الفئة 3، كان لدينا نظام VLT محدود لمدة عامين. في نظامنا، الذي كانت تديره SDG (وهي الآن جزء من Bally)، بدأ مجموع الجوائز بأربعة ملايين سحب. عندما خُفِّض مجموع الجوائز وتبقى مليونان، أُضيفت الجائزة التالية، وهي 4 ملايين، ليصل المجموع الإجمالي إلى ستة ملايين سحب. وعندما خُفِّض مجموع الجوائز إلى مليونين مرة أخرى، تكررت العملية.
ما هو العدد المتوقع من اللفات اللازمة للحصول على ياتزيه؟
بافتراض أن اللاعب يحمل دائمًا الرقم الأكثر تمثيلًا، يكون المتوسط ١١٫٠٩. فيما يلي جدول يوضح توزيع عدد الرميات على محاكاة عشوائية لـ ٨٢٫٦ مليون محاولة.
تجربة ياتزي
| لفات | الحوادث | احتمال |
| 1 | 63908 | 0.00077371 |
| 2 | 977954 | 0.0118396 |
| 3 | 2758635 | 0.0333975 |
| 4 | 4504806 | 0.0545376 |
| 5 | 5776444 | 0.0699327 |
| 6 | 6491538 | 0.0785901 |
| 7 | 6727992 | 0.0814527 |
| 8 | 6601612 | 0.0799227 |
| 9 | 6246388 | 0.0756221 |
| 10 | 5741778 | 0.0695131 |
| 11 | 5174553 | 0.0626459 |
| 12 | 4591986 | 0.0555931 |
| 13 | 4022755 | 0.0487016 |
| 14 | 3492745 | 0.042285 |
| 15 | 3008766 | 0.0364257 |
| 16 | 2577969 | 0.0312103 |
| 17 | 2193272 | 0.0265529 |
| 18 | 1864107 | 0.0225679 |
| 19 | 1575763 | 0.019077 |
| 20 | 1329971 | 0.0161013 |
| 21 | 1118788 | 0.0135446 |
| 22 | 940519 | 0.0113864 |
| 23 | 791107 | 0.00957757 |
| 24 | 661672 | 0.00801056 |
| 25 | 554937 | 0.00671837 |
| 26 | 463901 | 0.00561624 |
| 27 | 387339 | 0.00468933 |
| 28 | 324079 | 0.00392347 |
| 29 | 271321 | 0.00328476 |
| 30 | 225978 | 0.00273581 |
| 31 | 189012 | 0.00228828 |
| 32 | 157709 | 0.00190931 |
| 33 | 131845 | 0.00159619 |
| 34 | 109592 | 0.00132678 |
| 35 | 91327 | 0.00110565 |
| 36 | 76216 | 0.00092271 |
| 37 | 63433 | 0.00076795 |
| 38 | 52786 | 0.00063906 |
| 39 | 44122 | 0.00053417 |
| 40 | 36785 | 0.00044534 |
| 41 | 30834 | 0.00037329 |
| 42 | 25494 | 0.00030864 |
| 43 | 21170 | 0.0002563 |
| 44 | 17767 | 0.0002151 |
| 45 | 14657 | 0.00017745 |
| 46 | 12410 | 0.00015024 |
| 47 | 10299 | 0.00012469 |
| 48 | 8666 | 0.00010492 |
| 49 | 7355 | 0.00008904 |
| 50 | 5901 | 0.00007144 |
| 51 | 5017 | 0.00006074 |
| 52 | 4227 | 0.00005117 |
| 53 | 3452 | 0.00004179 |
| 54 | 2888 | 0.00003496 |
| 55 | 2470 | 0.0000299 |
| 56 | 2012 | 0.00002436 |
| 57 | 1626 | 0.00001969 |
| 58 | 1391 | 0.00001684 |
| 59 | 1135 | 0.00001374 |
| 60 | 924 | 0.00001119 |
| 61 | 840 | 0.00001017 |
| 62 | 694 | 0.0000084 |
| 63 | 534 | 0.00000646 |
| 64 | 498 | 0.00000603 |
| 65 | 372 | 0.0000045 |
| 66 | 316 | 0.00000383 |
| 67 | 286 | 0.00000346 |
| 68 | 224 | 0.00000271 |
| 69 | 197 | 0.00000238 |
| 70 | 160 | 0.00000194 |
| 71 | 125 | 0.00000151 |
| 72 | 86 | 0.00000104 |
| 73 | 79 | 0.00000096 |
| 74 | 94 | 0.00000114 |
| 75 | 70 | 0.00000085 |
| 76 | 64 | 0.00000077 |
| 77 | 38 | 0.00000046 |
| 78 | 42 | 0.00000051 |
| 79 | 27 | 0.00000033 |
| 80 | 33 | 0.0000004 |
| 81 | 16 | 0.00000019 |
| 82 | 18 | 0.00000022 |
| 83 | 19 | 0.00000023 |
| 84 | 14 | 0.00000017 |
| 85 | 6 | 0.00000007 |
| 86 | 4 | 0.00000005 |
| 87 | 9 | 0.00000011 |
| 88 | 4 | 0.00000005 |
| 89 | 5 | 0.00000006 |
| 90 | 5 | 0.00000006 |
| 91 | 1 | 0.00000001 |
| 92 | 6 | 0.00000007 |
| 93 | 1 | 0.00000001 |
| 94 | 3 | 0.00000004 |
| 95 | 1 | 0.00000001 |
| 96 | 1 | 0.00000001 |
| 97 | 2 | 0.00000002 |
| 102 | 1 | 0.00000001 |
| المجموع | 82600000 | 1 |
هل تعرف أي موقع يحتوي على تحليل جيد لاحتمالات/إحصائيات/فرص لعبة الطاولة، وهل هناك أي كتب معينة يمكنك التوصية بها حول أي جانب من جوانب اللعبة؟
الطاولة من ألعاب القمار المفضلة لدي. لا أكتب عنها لأن ألعاب اللاعبين ضد بعضهم البعض صعبة التحليل. كما أنني لا أجد أي مجال جديد لأتقدم فيه. لذا، سأترك النصائح للآخرين. إليكم مصادري المقترحة:
الطاولة بقلم بول ماجرييل: لو كان هناك كتاب مقدس عن الطاولة، لكان هذا هو. أنا فخور بامتلاكي نسخة قديمة بغلاف مقوى. سيكون هذا الكتاب نقطة انطلاق رائعة. على الرغم من أنه كُتب عام ١٩٧٦، إلا أن نصائحه لا تزال قيّمة.
٥٠١ مسألة أساسية في لعبة الطاولة بقلم بيل روبرتي: أحاول قراءة هذا الكتاب منذ سنوات، وما زلت في منتصف الطريق. من المُحبط أن أخطئ في نصف المسائل، لدرجة تجعلني أعتقد أنني سيئ في لعبة الطاولة كما هو الحال في لعبة الغولف. مع ذلك، مع كل مسألة أغفلها، هناك درسٌ قيّمٌ يجب تعلمه. يُعد هذا الكتاب أداةً تعليميةً قيّمةً ومُشجعةً للاعبين من المستوى المتوسط إلى المتقدم.
برنامج طاولة سنوي : ألعب حوالي ألف لعبة سنويًا ضد هذه اللعبة. لا يقتصر برنامج سنوي على تقديم أداء شبه مثالي فحسب، بل يُخبرك أيضًا بدقة بمدى تكلفة أخطائك عند ارتكابها. هناك العديد من الميزات الأخرى التي لم أستكشفها من قبل. إذا كان هناك شيء واحد تعلمته من سنوي، فهو أن أكبر مشكلة في لعبتي هي الأخطاء الفادحة التي قد تؤدي أحيانًا إلى عدم وضوح الحركات تمامًا. وكما هو الحال في الشطرنج، فإن حركة خاطئة واحدة قد تُلغي مئة حركة جيدة.
موقع موتيف : قبل شراء سنوي، لعبتُ عددًا لا يُحصى من الألعاب ضد موتيف. استراتيجية موتيف فعّالة جدًا، برأيي. لا شيء يُضاهي اللعب ضد خصم أقوى لتحسين أدائك.
في عمود ١١ أبريل ٢٠٠٤، طُرح سؤال حول الاستراتيجية الصحيحة في عرض "السعر مناسب". بافتراض اتباع الاستراتيجية المثلى، ما احتمال فوز كل لاعب؟
يوضح الجدول التالي احتمالية فوز كل لاعب، وفقًا للدورة الأولى للاعب الأول، حيث يبدأ اللاعب 1 أولاً، يليه اللاعب 2، ثم اللاعب 3. يوضح الصف السفلي إجمالي احتمالات الفوز قبل الدورة الأولى.
احتمالات في عرض السعر الصحيح
| الدوران 1 | الاستراتيجية | اللاعب 1 | اللاعب 2 | اللاعب 3 |
| 0.05 | يلف | 20.59% | 37.55% | 41.85% |
| 0.10 | يلف | 20.59% | 37.55% | 41.86% |
| 0.15 | يلف | 20.57% | 37.55% | 41.87% |
| 0.20 | يلف | 20.55% | 37.55% | 41.9% |
| 0.25 | يلف | 20.5% | 37.56% | 41.94% |
| 0.30 | يلف | 20.43% | 37.56% | 42.01% |
| 0.35 | يلف | 20.33% | 37.58% | 42.10% |
| 0.40 | يلف | 20.18% | 37.60% | 42.22% |
| 0.45 | يلف | 19.97% | 37.64% | 42.39% |
| 0.50 | يلف | 19.68% | 37.71% | 42.61% |
| 0.55 | يلف | 19.26% | 37.81% | 42.93% |
| 0.60 | يلف | 18.67% | 37.96% | 43.36% |
| 0.65 | يلف | 17.86% | 38.21% | 43.93% |
| 0.70 | يقضي | 21.56% | 38.28% | 40.16% |
| 0.75 | يقضي | 28.42% | 35.21% | 36.38% |
| 0.80 | يقضي | 36.82% | 31.26% | 31.92% |
| 0.85 | يقضي | 46.99% | 26.35% | 26.66% |
| 0.90 | يقضي | 59.17% | 20.36% | 20.47% |
| 0.95 | يقضي | 73.61% | 13.19% | 13.21% |
| 1.00 | يقضي | 90.57% | 4.72% | 4.72% |
| متوسط | 30.82% | 32.96% | 36.22% |
إليكم عدد التركيبات الفائزة من أصل 6×20 6 ممكنة.
اللاعب 1: 118,331,250اللاعب 2: 126,566,457
اللاعب 3: 139,102,293
ما هي الاستراتيجية الصحيحة لرهان "آسي ديوسي" في لعبة البوكر المنزلية؟ طريقة اللعب هي: إذا تطابقت الورقة الثالثة مع إحدى الورقتين الأوليين، يكون الرهان متعادلاً.
طريقة اللعب، حيث تكون مباراة البطاقة الثالثة متعادلة، تميل احتمالات الفوز لصالحك عندما يكون هناك ستة صفوف على الأقل بين أول بطاقتين (فارق ست بطاقات). كما لعبتُ في مقاطعة أورانج، كانت مباراة البطاقة الثالثة تؤدي إلى خسارة مضاعفة. بموجب هذه القاعدة، تكون احتمالات الفوز متعادلة مع فارق ثماني بطاقات. إذا انتهت مباراة البطاقة الثالثة بخسارة مضاعفة، فأنت بحاجة إلى فارق سبع بطاقات لتكون احتمالات الفوز في صالحك.
لعبة بوكر الورقة الواحدة تتكون من ثلاث أوراق: الآس، والاثنين، والثلاثي. الآس هو الأقل قيمةً والثلاثي هو الأعلى قيمةً. يضع كل لاعب دولاراً واحداً في الرهان. ثم يحصل كل لاعب على ورقة واحدة. ترتيب الرهانات محدد مسبقاً، حيث يبدأ اللاعب الأول بالرهان. يمكن للاعب الأول إما المراهنة بدولار واحد أو الشيك. إذا راهن اللاعب الأول، يمكن للاعب الثاني إما المراهنة بدولار واحد أو الشيك. إذا راهن اللاعب الأول، وراهن اللاعب الثاني، يمكن للاعب الأول المراهنة بدولار واحد أو الشيك. إذا راهن اللاعب الأول، وراهن اللاعب الثاني، يمكن للاعب الأول المراهنة بدولار واحد أو الشيك. إذا راهن اللاعبان، أو راهن كلاهما، تفوز الورقة الأعلى بالرهان. بافتراض أن كلا اللاعبين منطقيان، ما هي الاستراتيجية الأمثل لكل لاعب؟
أتمنى أن تكون سعيدًا؛ فقد قضيتُ اليوم كله في هذا. تجد الإجابة والحل على موقعي الآخر mathproblems.info ، أو على المسألة ٢٠٣، أو على الورقة الأكاديمية "نظرية الألعاب والبوكر" لجيسون سوانسون.
أبحث عن قرض عقاري. إحدى الشركات تعرض سعر فائدة ٥.٧٥٪، مضافًا إليه نقطة مئوية، على قرض ثابت لمدة ٣٠ عامًا. وأخرى تفرض سعر فائدة ٥.٨٧٥٪ بدون نقطة مئوية. أيهما أفضل؟
لمصلحة القراء الآخرين، النقطة هي عمولة تُفرض على القرض. على سبيل المثال، في قرض بقيمة 250,000 دولار أمريكي، تُعادل النقطة 2,500 دولار أمريكي. سأفترض أن المقترض سيضيف النقطة إلى رصيده الأصلي، ولن يُسدد أصل القرض مُبكرًا.
الجدول التالي يبين سعر الفائدة المكافئ بدون النقطة، وفقاً لسعر الفائدة بنقطة واحدة والأجل.
معدل فائدة مكافئ بدون نقاط
| سعر الفائدة بنقطة واحدة | 10 سنوات | 15 سنة | 20 سنة | 30 سنة | 40 سنة |
| 4.00% | 4.212% | 4.147% | 4.115% | 4.083% | 4.067% |
| 4.25% | 4.463% | 4.398% | 4.366% | 4.334% | 4.318% |
| 4.50% | 4.714% | 4.649% | 4.617% | 4.585% | 4.570% |
| 4.75% | 4.965% | 4.900% | 4.868% | 4.836% | 4.821% |
| 5.00% | 5.216% | 5.151% | 5.119% | 5.088% | 5.073% |
| 5.25% | 5.467% | 5.402% | 5.370% | 5.339% | 5.324% |
| 5.50% | 5.718% | 5.654% | 5.621% | 5.590% | 5.576% |
| 5.75% | 5.969% | 5.905% | 5.873% | 5.842% | 5.827% |
| 6.00% | 6.220% | 6.156% | 6.124% | 6.093% | 6.079% |
| 6.25% | 6.471% | 6.407% | 6.375% | 6.344% | 6.330% |
| 6.50% | 6.723% | 6.658% | 6.626% | 6.596% | 6.582% |
| 6.75% | 6.974% | 6.909% | 6.878% | 6.847% | 6.834% |
| 7.00% | 7.225% | 7.160% | 7.129% | 7.099% | 7.085% |
| 7.25% | 7.476% | 7.412% | 7.380% | 7.350% | 7.337% |
| 7.50% | 7.727% | 7.663% | 7.631% | 7.602% | 7.589% |
| 7.75% | 7.978% | 7.914% | 7.883% | 7.853% | 7.841% |
| 8.00% | 8.229% | 8.165% | 8.134% | 8.105% | 8.093% |
| 8.25% | 8.480% | 8.416% | 8.385% | 8.357% | 8.344% |
| 8.50% | 8.731% | 8.668% | 8.637% | 8.608% | 8.596% |
| 8.75% | 8.982% | 8.919% | 8.888% | 8.860% | 8.848% |
| 9.00% | 9.233% | 9.170% | 9.140% | 9.112% | 9.100% |
| 9.25% | 9.485% | 9.421% | 9.391% | 9.363% | 9.352% |
| 9.50% | 9.736% | 9.673% | 9.642% | 9.615% | 9.604% |
| 9.75% | 9.987% | 9.924% | 9.894% | 9.867% | 9.856% |
| 10.00% | 10.238% | 10.175% | 10.145% | 10.119% | 10.108% |
يُظهر هذا أن معدل فائدة ٥.٧٥٪ مع نقطة واحدة يُعادل ٥.٨٤٢٪ بدون نقاط. بمعنى آخر، سيكون الدفع متساويًا في كلا الحالتين، بافتراض إضافة النقطة المُضافة إلى الرصيد الأصلي. كان عرضك الآخر ٥.٨٧٥٪ بدون نقاط، وهو أعلى من ٥.٨٤٢٪، لذا سأقبل ٥.٧٥٪ مع النقطة.
PS: بالنسبة لأولئك منكم الذين يتساءلون عن كيفية حل i، فقد استخدمت وظيفة المعدل في Excel.
ابني نجح في حفرتين في ملعب واحد خلال أسبوعين. ما هي احتمالات نجاحه؟ ابني لديه إعاقة واحدة. الأولى ١٥١ ياردة والثانية ١٣٧ ياردة، في ملعبين مختلفين.
وفقًا لكتاب Life: the Odds (and How to Improve Them) بقلم جريجوري بير، فإن احتمالات الحصول على حفرة واحدة في حفرة ذات ثلاث ضربات في جولة PGA هي 1 من 2491. أعتقد أن هذه المسافات تقع ضمن نطاق الثلاث ضربات.
إن معدل إعاقة واحد جيد جدًا، لذا لن أقدم خصمًا كبيرًا مقارنةً بلاعبي جولة PGA. لنفترض أن احتمالية فوز ابنك في كل حفرة من 3 بار هي 1 من 3000. عادةً ما يحتوي ملعب الجولف الذهبي على حوالي أربعة حفر من 3 بار. لنفترض أن ابنك يلعب يوميًا، أي 28 حفرة من 3 بار أسبوعيًا. احتمالية الفوز بحفرتين بالضبط في حفرة واحدة هي (28،2) × (1/3000) 2 × (2999/3000) 26 = 1 من 24017.
شاركتُ مؤخرًا في سحب على 7033 جائزة، ويُقال إن احتمال الفوز بها هو 1 من 13. اشتريتُ 5 تذاكر. ما هي احتمالاتي الفعلية للفوز؟ هناك أيضًا 40 جائزة كبيرة. ما هي احتمالاتي للفوز بجائزة كبيرة؟
لتبسيط الأمر، دعونا نتجاهل حقيقة أنه كلما زادت التذاكر التي تشتريها، انخفضت قيمة كل تذكرة لأنك تتنافس مع نفسك. مع ذلك، فإن احتمال خسارة جميع التذاكر الخمس هو (١٢/١٣) ٥ = ٦٧.٠٢٪. لذا، فإن احتمال الفوز بجائزة واحدة على الأقل هو ٣٢.٩٨٪. يوجد ٧٠٣٣ × ١٣ = ٩١٤٢٩ تذكرة إجمالية في الأسطوانة قبل شراء أي منها. ٩١٤٢٩ - ٤٠ = ٩١٣٨٩ ليست جوائز كبيرة. واحتمال عدم الفوز بأي جوائز كبيرة بخمس تذاكر هو (٩١٣٨٩ / ٩١٤٢٩) ٥ = ٩٩.٧٨٪. لذا، فإن احتمال الفوز بجائزة كبيرة واحدة على الأقل هو ٠.٢٢٪، أو ١ من ٤٥٨.
في لعبة القلوب، يُعطى كل لاعب ١٣ ورقة. تُسمى الورقة التي تحتوي على أكبر عدد من الأوراق "الورقة الطويلة"، والتي يمكن أن تحتوي على من ٤ إلى ١٣ ورقة. ما احتمالية كل من هذه النتائج؟
احتمالات البدلة الطويلة في القلوب
| بطاقات | التركيبات | احتمال |
| 4 | 222766089260 | 0.35080524800183 |
| 5 | 281562853572 | 0.44339660045899 |
| 6 | 105080049360 | 0.16547685914958 |
| 7 | 22394644272 | 0.03526640326564 |
| 8 | 2963997036 | 0.00466761219692 |
| 9 | 235237860 | 0.00037044541245 |
| 10 | 10455016 | 0.00001646424055 |
| 11 | 231192 | 0.00000036407412 |
| 12 | 2028 | 0.00000000319363 |
| 13 | 4 | 0.00000000000630 |
| المجموع | 635013559600 | 1 |
تنص قاعدة ٧٢ على تقسيم معدل العائد السنوي على ٧٢، وهذا يُعطيك عدد السنوات اللازمة لمضاعفة أموالك. على سبيل المثال، استثمارٌ يُدرّ ١٠٪ سنويًا سيستغرق ٧٢/١٠ = ٧.٢ سنوات لمضاعفة قيمته. سؤالي البسيط هو: لماذا ٧٢؟
أولاً، "قاعدة 72" هي تقدير تقريبي للمدة اللازمة لمضاعفة أموالك، وليست إجابة دقيقة. يوضح الجدول التالي قيم "قاعدة 72" وعدد السنوات بدقة، لمعدلات فائدة سنوية مختلفة.
قاعدة الـ 72 - سنوات لمضاعفة المال
| سعر الفائدة | قاعدة 72 | بالضبط | اختلاف |
|---|---|---|---|
| 0.01 | 72.00 | 69.66 | 2.34 |
| 0.02 | 36.00 | 35.00 | 1.00 |
| 0.03 | 24.00 | 23.45 | 0.55 |
| 0.04 | 18.00 | 17.67 | 0.33 |
| 0.05 | 14.40 | 14.21 | 0.19 |
| 0.06 | 12.00 | 11.90 | 0.10 |
| 0.07 | 10.29 | 10.24 | 0.04 |
| 0.08 | 9.00 | 9.01 | -0.01 |
| 0.09 | 8.00 | 8.04 | -0.04 |
| 0.10 | 7.20 | 7.27 | -0.07 |
| 0.11 | 6.55 | 6.64 | -0.10 |
| 0.12 | 6.00 | 6.12 | -0.12 |
| 0.13 | 5.54 | 5.67 | -0.13 |
| 0.14 | 5.14 | 5.29 | -0.15 |
| 0.15 | 4.80 | 4.96 | -0.16 |
| 0.16 | 4.50 | 4.67 | -0.17 |
| 0.17 | 4.24 | 4.41 | -0.18 |
| 0.18 | 4.00 | 4.19 | -0.19 |
| 0.19 | 3.79 | 3.98 | -0.20 |
| 0.20 | 3.60 | 3.80 | -0.20 |
لماذا ٧٢؟ ليس بالضرورة أن يكون ٧٢ بالضبط. هذا هو الرقم المناسب لمعدلات الفائدة الواقعية التي من المرجح أن تراها على أي استثمار. وهو يُطابق تقريبًا معدل فائدة ٧٫٨٤٦٩٪. لا يوجد شيء مميز في ٧٢، كما هو الحال مع π أو e. لماذا يُجدي أي رقم نفعًا؟ إذا كان معدل الفائدة هو i، فلنحسب عدد السنوات (y) اللازمة لمضاعفة الاستثمار.
2 = (1+i) y
ln(2)= ln(1+i) y
ln(2)= y×ln(1+i)
y = ln(2)/ln(1+i)
قد لا تكون هذه أفضل إجابة لي على الإطلاق، ولكن حاول اتباع هذا المنطق: دع y = ln (x).
dy/dx=1/x.
1/x =~ x عند قيم x قريبة من 1.
وبالتالي فإن dy/dx =~ 1 لقيم x القريبة من 1.
وبالتالي فإن ميل ln(x) سيكون قريبًا من 1 لقيم x القريبة من 1.
وبالتالي فإن ميل ln(1+x) سيكون قريبًا من 1 لقيم x القريبة من 0.
تقول "قاعدة 72" أن .72/i =~ .6931/ln(1+i).
لقد أثبتنا أن i وln(1+i) متشابهتان لقيم i القريبة من 0.
لذا فإن 1/i و1/ln(1+i) متشابهان لقيم i القريبة من 0.
يؤدي استخدام 72 بدلاً من 69.31 إلى تعديل الاختلافات بين i وln(1+i) لقيم i حوالي 8%.
آمل أن يكون هذا منطقيًا. حساباتي صدئة نوعًا ما؛ استغرق شرح هذا لنفسي ساعات.
تم طرح هذا السؤال ومناقشته في منتدى موقعي المرافق Wizard of Vegas .
في معرض شعبي أقيم مؤخرًا، أُقيمت لعبةٌ فيها حقلٌ من الأرقام، وفيه أكوابٌ سطحيةٌ وكوبٌ من الكرات، وتتضمن اللعبة جمعًا. لم أسأل عن اسم اللعبة، وبحثتُ عنها على الإنترنت لساعةٍ تقريبًا، لكنني لم أجد شيئًا عنها. ظننتُ أن لديكم بعض المعلومات عنها، أو عن احتمالاتها، أو على الأقل اسمها.
يُطلق على هذه اللعبة في عالم الصناعة اسم "رازل دازل". أتذكر رؤيتها في جنوب كاليفورنيا عندما كنت طفلاً، والعام الماضي في سان فيليبي، المكسيك. عادةً ما تُصمَّم لتبدو وكأنها لعبة كرة قدم. هذه اللعبة، في رأيي، أسوأ عمليات الاحتيال في ألعاب الكرنفال. يجب أن تخجل ولاية نيويورك من السماح بها. بناءً على بعض الأبحاث، تختلف القواعد من مكان لآخر، لكن جوهر الاحتيال يبقى واحدًا دائمًا.
يعتمد هذا الرهان على نفس وهم رهان الحقل في لعبة الكرابس. لمن لا يعرف رهان الحقل، يفوز اللاعب إذا كان مجموع رميتي نرد 2، 3، 4، 9، 10، 11، أو 12. الأرقام الخاسرة هي 5، 6، 7، و8. تُدفع أرباح متساوية في كل رهان، باستثناء الرقم 2 الذي يدفع 2 إلى 1، والرقم 12 الذي يدفع 3 إلى 1 (باستثناء كازينوهات هارا البخيلة، حيث تدفع 2 إلى 1 فقط على الرقم 12). قد يظن المقامر الذي لا يملك خبرة في الرياضيات أن هذا رهان جيد، لأن هناك 7 أرقام فائزة و4 أرقام خاسرة فقط. والسبب في أن احتمالات الفوز في صالح الكازينو هي أن الأرقام الخاسرة لديها أكبر فرصة للفوز.
فيما يلي القواعد المحددة للعبة Razzle Dazzle، كما تم أخذها من المقال "احتمالات الفوز في لعبة كرنفال معينة" بقلم دونالد أ. بيري ورونالد ر. ريجال، والذي ظهر في عدد نوفمبر 1978 من مجلة The American Statistician.
- هدف اللعبة هو التقدم مسافة 100 ياردة عبر ملعب كرة القدم. سيحصل اللاعب على جائزة قيّمة عند تحقيق ذلك.
- يبدأ اللاعب بدفع رسوم محددة لكل لعبة، مثل 1 دولار.
- سيُسقط اللاعب ٨ كرات زجاجية على شبكة ١١ × ١٣. ستسقط كل كرة زجاجية في إحدى الثقوب الـ ١٤٣.
- تحتوي كل حفرة على عدد من النقاط من 1 إلى 6. يوضح الجدول التالي تكرار كل عدد من النقاط.
توزيع نقاط رازل دازل
نقاط رقم
صعد على متنهااحتمال 1 11 0.076923 2 19 0.132867 3 39 0.272727 4 44 0.307692 5 19 0.132867 6 11 0.076923 المجموع 143 1.000000 - سيتم إضافة إجمالي النقاط. سيبحث الكارنيه عن إجمالي النقاط في جدول التحويل لمعرفة عدد الياردات التي قطعها اللاعب. يظهر جدول التحويل أدناه.
مخطط تحويل رازل دازل
نقاط ياردات
اكتسبت8 100 9 100 10 50 11 30 12 50 13 50 14 20 15 15 16 10 17 5 من 18 إلى 38 0 39 5 40 5 41 15 42 20 43 50 44 50 45 30 46 50 47 100 48 100 - إذا حصل اللاعب على مجموع 29، فسيتم مضاعفة الرسوم لجميع الرميات اللاحقة، وسيتم منح اللاعب جائزة إضافية إذا وصل إلى الطرف الآخر من ملعب كرة القدم.
متوسط النقاط لكل كرة زجاجية هو 3.52، والانحراف المعياري هو 1.31. لاحظ أن احتمالية الحصول على 3 و4 نقاط هي الأعلى. هذا يُبقي الانحراف المعياري منخفضًا، ومجموع الكرات الزجاجية قريبًا من التوقعات. بالمقارنة، الانحراف المعياري لرمية نرد واحدة هو 1.71.
لاحظ الآن وجود ٢٠ مجموع فوز و٢١ مجموع خسارة في جدول تحويل المسافات. قد يظنّ المراهنون على ألعاب الكرنفال، وهم ساذجون، أن احتمالية فوزهم هي ٢٠/٤١ أو ٤٨.٨٪. لن أتفاجأ إذا ادّعى أصحاب الكازينو زورًا أن هذه هي احتمالات الفوز. مع ذلك، وكما هو الحال في رهان الميدان، فإن النتائج الأكثر احتمالية لا تفوز بأي شيء.
يوضح الجدول التالي احتمالية كل عدد من النقاط في كل دورة، والمسافات المكتسبة، والمسافات المتوقعة. تُظهر الخلية السفلية اليمنى أن متوسط المسافة المكتسبة في كل دورة هو 0.0196.
الياردات المتوقعة المكتسبة في كل دورة
| نقاط | احتمال | ياردات اكتسبت | مُتوقع ياردات اكتسبت |
| 8 | 0.00000000005 | 100 | 0.00000000464 |
| 9 | 0.00000000176 | 100 | 0.00000017647 |
| 10 | 0.00000002586 | 50 | 0.00000129285 |
| 11 | 0.00000022643 | 30 | 0.00000679305 |
| 12 | 0.00000143397 | 50 | 0.00007169849 |
| 13 | 0.00000713000 | 50 | 0.00035650022 |
| 14 | 0.00002926510 | 20 | 0.00058530196 |
| 15 | 0.00010234709 | 15 | 0.00153520642 |
| 16 | 0.00031168305 | 10 | 0.00311683054 |
| 17 | 0.00083981462 | 5 | 0.00419907311 |
| 18 | 0.00202563214 | 0 | 0.00000000000 |
| 19 | 0.00441368617 | 0 | 0.00000000000 |
| 20 | 0.00874847408 | 0 | 0.00000000000 |
| 21 | 0.01586193216 | 0 | 0.00000000000 |
| 22 | 0.02642117465 | 0 | 0.00000000000 |
| 23 | 0.04056887936 | 0 | 0.00000000000 |
| 24 | 0.05757346716 | 0 | 0.00000000000 |
| 25 | 0.07566411880 | 0 | 0.00000000000 |
| 26 | 0.09221675088 | 0 | 0.00000000000 |
| 27 | 0.10431970222 | 0 | 0.00000000000 |
| 28 | 0.10958441738 | 0 | 0.00000000000 |
| 29 | 0.10689316272 | 0 | 0.00000000000 |
| 30 | 0.09677806051 | 0 | 0.00000000000 |
| 31 | 0.08125426057 | 0 | 0.00000000000 |
| 32 | 0.06317871335 | 0 | 0.00000000000 |
| 33 | 0.04540984887 | 0 | 0.00000000000 |
| 34 | 0.03009743061 | 0 | 0.00000000000 |
| 35 | 0.01833921711 | 0 | 0.00000000000 |
| 36 | 0.01023355162 | 0 | 0.00000000000 |
| 37 | 0.00520465303 | 0 | 0.00000000000 |
| 38 | 0.00239815734 | 0 | 0.00000000000 |
| 39 | 0.00099365741 | 5 | 0.00496828705 |
| 40 | 0.00036673565 | 5 | 0.00183367827 |
| 41 | 0.00011909673 | 15 | 0.00178645089 |
| 42 | 0.00003349036 | 20 | 0.00066980729 |
| 43 | 0.00000797528 | 50 | 0.00039876403 |
| 44 | 0.00000155945 | 50 | 0.00007797235 |
| 45 | 0.00000023832 | 30 | 0.00000714969 |
| 46 | 0.00000002632 | 50 | 0.00000131607 |
| 47 | 0.00000000176 | 100 | 0.00000017647 |
| 48 | 0.00000000005 | 100 | 0.00000000464 |
| المجموع | 1.00000000000 | 0 | 0.01961648451 |
فيما يلي بعض نتائج المحاكاة العشوائية لـ 17.5 مليون لعبة.
نتائج محاكاة رازل دازل
| سؤال | إجابة |
| احتمال التقدم في كل دورة | 0.0028 |
| الياردات المتوقعة المكتسبة في كل دورة | 0.0196 |
| الياردات المتوقعة المكتسبة لكل تقدم | 6.9698 |
| عدد الأدوار المتوقعة لكل لعبة | 5238.7950 |
| متوسط الضربات الثنائية في كل مباراة | 559.9874 |
| متوسط الجوائز لكل لعبة | 560.9874 |
كنت أود الإشارة إلى متوسط إجمالي الرهان لكل لعبة، لكن جهازي لا يستطيع التعامل مع أرقام كبيرة كهذه. في اللعبة المتوسطة، ضاعف اللاعب رهانه 560 مرة خلال متوسط 5239 دورة في اللعبة. في إحدى ألعاب المحاكاة، ضاعف اللاعب رهانه 1800 مرة. حتى مع متوسط 560 ضعفًا، سيكون الرهان لكل رمية 3.77 دولار × 10 168 ، بافتراض رهان ابتدائي بقيمة دولار واحد. هذا أكبر بكثير من عدد الذرات في الكون المعروف ( المصدر ).
حتى أكثر اللاعبين سذاجةً لن يلعبوا طويلًا إذا كان يتقدم مرة واحدة كل 355 لعبة فقط. ما سيفعله عاملو الكازينو هو الغش لصالح اللاعب في البداية. قد يلاحظون رميات اللاعب المجانية، أو يكذبون في جمع النقاط، مما يمنح اللاعب مجموع نقاط الفوز لتعزيز ثقته بنفسه. لم ألعب هذه اللعبة من قبل، لكنني أتخيل أنه عندما يقترب اللاعب من المنطقة الحمراء (20 ياردة أو أقل من الهبوط)، سيبدأ عامل الكازينو باللعب بنزاهة. قد يتساءل اللاعب عن سبب عدم تحقيقه أي تقدم مفاجئ، ولكن مع استثماره للمال بالفعل، وقربه الشديد من خط النهاية، سيتردد في الانسحاب والتخلي عن المسافة التي دفع ثمنها بالفعل.
الروابط
- رازل دازل ، مقتطف من كتاب "على الطريق".
- لعبة Razzle Dazzle Carny Board Game Arcade Scam .
- احتمالات الفوز في لعبة كرنفال معينة بقلم دونالد أ. بيري ورونالد ر. ريجال
عُرضت لعبةٌ على غرار لعبة "إكس أو" في كرنفالٍ حديث. مقابل جنيه إسترليني واحد، تُقذف ثلاث كراتٍ فائقة النطاط نحو صندوقٍ خشبيٍّ كبيرٍ ذي تسعة جيوبٍ في أسفله. بافتراض أن كل كرةٍ سقطت في مربعٍ مُحدد، ما احتمال الفوز؟
هناك ثماني طرق للفوز: ثلاثة صفوف، ثلاثة أعمدة، وقطران. هناك مجموع (9، 3) = 84 طريقة لاختيار 3 مربعات من أصل 9. لذا، فإن احتمال الفوز هو 8/84 = 9.52%.
تم طرح هذا السؤال ومناقشته في منتدى موقعي المرافق Wizard of Vegas .
ما هي نصيحتك للعب المونوبولي؟
هذه هي الاستراتيجية الأساسية التي يتبعها ساحري في لعبة المونوبولي:
- اشترِ كل شيء. قد يستثني اللاعبون المتقدمون العقار إذا لم يُمكّنك من تحقيق احتكار، أو منع شخص آخر، أو إذا كانت قيمته ضئيلة كورقة مساومة. كما يُمكن رفض شراء المرافق في حالة نقص السيولة.
- تاجر بأفضل ما يمكنك. هنا تبرز المهارة. حاول التداول للحصول على أفضل مجموعة ممكنة. إليك ترتيبي لها بشكل عام: برتقالي، أصفر، أزرق فاتح، أزرق داكن، بنفسجي فاتح، أحمر، أخضر، بنفسجي داكن. يختلف هذا الترتيب باختلاف الظروف. في لعبة ذات ميزانية محدودة، اختر المجموعات الأرخص في التطوير، مثل الأزرق الفاتح. أما في لعبة ذات ميزانية غنية، فاختر المجموعات التي توفر إمكانية إنفاق المال عليها، مثل الأصفر أو الأزرق الداكن.
- بمجرد حصولك على مجموعة، سواءً بشكل طبيعي أو عن طريق المبادلة، ابدأ ببناء منزل بسرعة. حاول الوصول إلى ثلاثة منازل في كل عقار بأسرع وقت ممكن. سينخفض العائد الهامشي لكل منزل بعد ثلاثة منازل. رهِن معظم عقاراتك الأخرى وأنفق نقودك. من الأفضل أن تترك بعض رأس المال للنفقات الصغيرة. عدم إنفاق أموالك أشبه بجندي في المعركة لا يستخدم رصاصه.
- خالف جميع قواعد اللعبة السخيفة. ينطبق هذا تحديدًا على جائزة الموقف المجاني (لا أطيقها!). إذا كنت أكثر مهارة من خصومك، فعليك تقليل عشوائية اللعبة.
إذا كان قرد يلعب بمكعب روبيك، ما هي احتمالات وجوده في النمط المحلول في أي وقت معين؟
الوجوه المركزية الستة للمكعب ثابتة. بتدوير الوجوه، كل ما يمكنك فعله هو إعادة ترتيب الزوايا والحواف. إذا فككتَ المكعب، فسيكون هناك 8 طرق لترتيب الزوايا الثمانية، بغض النظر عن اتجاه كل قطعة. وبالمثل، هناك 12 طريقة لترتيب الحواف الاثني عشر، بغض النظر عن اتجاهها.
هناك ثلاث طرق لتوجيه كل زاوية، بإجمالي ٣ ⁸ = ٦٥٦١ اتجاهًا للزوايا. وبالمثل، هناك طريقتان لتوجيه كل حافة، بإجمالي ٢ ⁸ = ٤٠٩٦ اتجاهًا للحافة.
لذا، إذا فككنا المكعب وأعدنا ترتيب مجموعات الحواف والزوايا، فسيكون لدينا 8! × 12! × 3 8 × 2 12 = 519,024,039,293,878,000,000 تبديل ممكن. مع ذلك، لا يمكن الوصول إلى جميع هذه التبديلات من نقطة البداية بتدوير الوجوه.
أولًا، من المستحيل تدوير زاوية واحدة فقط وترك باقي القطع كما هي. لا يمكن لأي مجموعة من الدورات تحقيق ذلك. باختصار، لكل فعل رد فعل. إذا أردت تدوير زاوية واحدة، فسيؤدي ذلك إلى اضطراب القطع الأخرى بطريقة ما. وبالمثل، من المستحيل قلب قطعة حافة واحدة فقط. لهذه الأسباب، يجب قسمة عدد التباديل على 3 × 2 = 6.
ثانيًا، من المستحيل تبديل قطعتين من الحافة دون إزعاج باقي المكعب. هذا هو الجزء الأصعب في هذه الإجابة للشرح. كل ما يمكنك فعله بمكعب روبيك هو تدوير وجه واحد في كل مرة. كل حركة تدور أربع قطع من الحافة وأربع قطع من الزوايا ليصبح المجموع ثماني قطع متحركة. يمكن تمثيل سلسلة الدورات بعدد من حركات القطع القابلة للقسمة على 8. غالبًا ما تؤدي سلسلة الحركات إلى إلغاء حركتين لبعضهما البعض. ومع ذلك، سيكون هناك دائمًا عدد زوجي من القطع المتحركة مع أي سلسلة من الدورات. إن تبديل قطعتين من الحافة سيكون حركة واحدة، وهو عدد فردي، لا يمكن تحقيقه بمجموع أي مجموعة من الأرقام الزوجية. سيطلق علماء الرياضيات على هذه مشكلة التكافؤ. لذلك يتعين علينا القسمة على 2 أخرى لأنه لا يمكن تبديل قطعتين من الحافة دون إزعاج القطع الأخرى.
إذن، هناك ١٢ مجموعة محتملة من تبديلات مكعب روبيك. إذا فككتَ مكعب روبيك وأعدتَ تركيبه عشوائيًا، فإن احتمال حله هو ١ من ١٢. لذا، فإن العدد الإجمالي للتبديلات في مكعب روبيك هو ٨! × ١٢! × ٣ ١٢ × ٢ ١٢ ÷ ١٢ = ٤٣,٢٥٢,٠٠٣,٢٧٤,٤٨٩,٩٠٠,٠٠٠. إذا كان لديك سبعة مليارات قرد، أي ما يعادل تقريبًا عدد سكان العالم، يلعبون عشوائيًا بمكعب روبيك، بمعدل دورة واحدة في الثانية، فسيمر المكعب عبر الموضع الذي تم حله مرة واحدة كل ١٩٦ عامًا في المتوسط.
الروابط
كنت ألعب هارتس، وتلقّيت ١٠ منها. ما هي احتمالات ذلك؟
لمن لا يعرف قواعد لعبة القلوب، تبدأ اللعبة بتوزيع ١٣ بطاقة على أربعة لاعبين. لنوع القلوب أهمية كبيرة في اللعبة، لذا فإن عدد البطاقات التي تحصل عليها مهم. يوضح الجدول التالي احتمالات الحصول على من ٠ إلى ١٣ بطاقة.
احتمالية الحصول على 0 إلى 13 قلبًا من أصل 13 بطاقة
| قلوب | التركيبات | احتمال | معكوس |
|---|---|---|---|
| 13 | 1 | 0.0000000000016 | 1 من 635,013,559,600.0 |
| 12 | 507 | 0.0000000007984 | 1 من 1,252,492,228.0 |
| 11 | 57,798 | 0.0000000910185 | 1 من 10,986,773.9 |
| 10 | 2,613,754 | 0.0000041160601 | 1 من 242,950.8 |
| 9 | 58,809,465 | 0.0000926113531 | 1 من 10,797.8 |
| 8 | 740,999,259 | 0.0011669030492 | 1 في 857.0 |
| 7 | 5,598,661,068 | 0.0088166008164 | 1 من 113.4 |
| 6 | 26,393,687,892 | 0.0415639752774 | 1 من 24.1 |
| 5 | 79,181,063,676 | 0.1246919258321 | 1 من 8.0 |
| 4 | 151,519,319,380 | 0.2386080062219 | 1 في 4.2 |
| 3 | 181,823,183,256 | 0.2863296074662 | 1 في 3.5 |
| 2 | 130,732,371,432 | 0.2058733541286 | 1 من 4.9 |
| 1 | 50,840,366,668 | 0.0800618599389 | 1 من 12.5 |
| 0 | 8,122,425,444 | 0.0127909480376 | 1 في 78.2 |
| المجموع | 635,013,559,600 | 1.0000000000000 |
تم طرح هذا السؤال ومناقشته في منتدى موقعي المرافق Wizard of Vegas .
بالنسبة لعروض الكازينو التي لا تزال تستخدم التذاكر العادية في أسطوانة حقيقية (وليس الإلكترونية)، حيث تطبع تذاكرك على مكتب اللاعبين وتضعها في الأسطوانة، هل تثني/تطوي تذاكرك قبل وضعها في الأسطوانة؟ هل تعتقد أن التذاكر المنحنية لديها فرصة أفضل للفوز؟
أتمنى أن تكون سعيدًا. للإجابة على هذا السؤال، اشتريتُ لفافة تذاكر كبيرة من متجر أوفيس ديبوت. ثم وضعتُ 500 تذكرة في كيس ورقي، نصفها مطوي إلى نصفين بزاوية 90 درجة تقريبًا، والنصف الآخر مفتوح. ثم طلبتُ من ستة متطوعين سحب ما بين 40 و60 تذكرة واحدة تلو الأخرى، مع استبدالها، بينما كنتُ أسجل النتائج. إليكم النتائج.
تجربة رسم التذكرة
| موضوع | مطوية | مكشوفة | المجموع |
|---|---|---|---|
| 1 | 25 | 25 | 50 |
| 2 | 38 | 22 | 60 |
| 3 | 25 | 15 | 40 |
| 4 | 34 | 16 | 50 |
| 5 | 27 | 23 | 50 |
| 6 | 26 | 24 | 50 |
| المجموع | 175 | 125 | 300 |
وبالتالي، تم طي 58.3% من التذاكر المسحوبة!
إذا افترضنا أن طيّ البطاقات لم يكن له تأثير، فإن هذه النتائج ستكون بعيدة عن التوقعات بمقدار 2.89 انحراف معياري. احتمال الحصول على هذا العدد من البطاقات المطوية، أو أكثر، بافتراض أن طيّ البطاقات لم يؤثر على احتمالات الفوز، هو 0.19%، أو 1 من 514.
أود أن أضيف أن المشاركين الذين سحبوا التذاكر على عجل كانوا أكثر عرضة لسحب بطاقات مطوية. أما أولئك الذين حرصوا على وقتهم في كل سحب، فكانت نسبة فوزهم متساوية تقريبًا.
لذا، استنتاجي هو بالتأكيد أن أطويهم.
لمناقشة هذا السؤال، يرجى زيارة منتدياتي في Wizard of Vegas .