WOO logo

يوصي المعالج

احتمال - النرد

إذا كنت تقوم برمي 6 أحجار نرد قياسية ذات ستة أوجه، ما هي احتمالات الحصول على ستة من نفس النوع؟

Jeff B. من Miami, Florida

الإجابة هي 6*(1/6) 6 = 6/46,656 = 1/7,776 =~ 0.0001286 .
ما هو متوسط عدد الرميات حتى يخرج اللاعب "سبعة"؟ أعلم أن الرقم 7 سيظهر كل 6 رميات، ولكن مع رميات "الخروج" 7-11 و"الكرابس"، بالإضافة إلى إمكانية حصول اللاعبين على نقاط متعددة، أعتقد أن متوسط عدد الرميات قد يكون أعلى من المتوقع. هل هناك أي مرجع رياضي في هذا الشأن؟

Grshooter من Kansas City, Missouri

متوسط عدد الرميات لكل لاعب هو 8.525510. لمعرفة احتمالية رميتين إلى 200 رمية بالضبط، يُرجى مراجعة صفحة احتمالية البقاء في لعبة الكرابس .
ما هي احتمالات (وتواتر) خسارة رهان DP في 100000 لفة من النرد (خط النرد/عدم المرور) 2x، 3x، 4x، 5x، 6x، 7x، 8x أو 9x على التوالي.

Derick من Minneapolis, USA

يوضح ملحق الكرابس كيفية حساب احتمالات أي رهان. ستجد هنا أن احتمال خسارة رهان "عدم المرور" هو ٢٩٢٨/٥٩٤٠. واحتمال خسارة n رهان متتالي هو (٢٩٢٨/٥٩٤٠) n . ويمكن تقريب تكرار الخسارة بالضبط n لكل ١٠٠,٠٠٠ رهان إلى ١٠٠,٠٠٠ × (٢٩٢٨/٥٩٤٠) n+٢ .
ما هي احتمالات الحصول على نفس الرقم باستخدام ستة أحجار نرد في رمية واحدة؟

Kyle Hill من Colstrip, Montana

احتمالات الحصول على ستة من نفس الرقم باستخدام ستة أحجار نرد هي 6*(1/6) 6 =1/7776 =~ 0.01286%.
كم مرة يمكنك رمي نرد ٢٨ مرة دون الحصول على ٧؟ كيف عرفت ذلك؟ تهانينا على موقعك الرائع.

Arturo G. من Mexico City, Mexico

شكراً على الإطراء. أعتقد أنك تقصد ما هو احتمال رمي حجري نرد ٢٨ مرة دون الحصول على ٧؟ احتمال عدم الحصول على ٧ في أي رمية هو ٥/٦. واحتمال عدم الحصول على ٧ في ٢٨ رمية هو (٥/٦) ٢٨ = ٠.٠٠٦٠٦٦، أو حوالي ١ من ١٦٥.
سؤال حول لعبة نرد شرقية، حيث يُفترض باللاعبين تخمين أي وجه من وجوه النرد سيظهر. يضع اللاعبون رهاناتهم أولاً على الأرقام 1، 2، 3، 4، 5، 6 (كما في الروليت)، ثم يقوم الموزع برمي 3 نرد في آنٍ واحد. تكون نسبة العائد 1:1 إذا ظهرت الأرقام المختارة مرة واحدة (على أيٍّ من النردات الثلاثة)، و2:1 إذا ظهر الرقم "لا" مرتين، و3:1 إذا ظهر الرقم المختار على جميع النردات الثلاثة. بما أن اللاعب يستطيع وضع أي عدد من الرهانات على اللوحة، فما هو العدد الأمثل للرهانات؟ (بافتراض أن جميع رهاناتي متساوية في الحجم)

Jansen من Toronto, Canada

احتمال مطابقة ثلاثة أرقام هو ١/٢١٦. احتمال مطابقتين هو ٣*٥/٢١٦. احتمال مطابقة واحدة هو ٢٥*٥/٢١٦. احتمال عدم مطابقة أي رقم هو ٥*٥*٥/٢١٦. لذا، فإن العائد المتوقع هو ٣*(١/٢١٦)+٢*(١٥/٢١٦)+١*(٧٥/٢١٦)-١*(١٢٥/٢١٦)=-١٧/٢١٦=-٧.٨٧٪. لا يوجد عدد مثالي للرهانات، وستخسر ٧.٨٧٪ من إجمالي قيمة الرهان مهما فعلت.

يمكن إجراء هذه الرهانات في كل من لعبة sic bo ولعبة chuck a luck .
سيد الساحر، ما هو احتمال الحصول على زوجين عند رمي أربعة نرد؟

Brian من St. Catherines, Canada

هناك 15 مجموعة أزواج مختلفة ممكنة. هناك 6 طرق لرمي النرد. هناك 6^4 = 1296 طريقة لرمي أربعة نرد. لذا، فإن الاحتمال هو 90/1296 = 6.9444%.
إذا رميتُ نردًا، فإن احتمال ظهور النتيجة ستة هو ١/٦. إذا رميتُ نردين، فهل يزداد احتمال ظهور النتيجة ستة على أحدهما، أم يبقى ١/٦؟

Mike R. من Rosemount

إذا رميتَ x نردًا، فإن احتمال الحصول على الرقم 6 مرة واحدة على الأقل هو 1-(5/6) 2. وفي حالة رمي نردين، تكون هذه النسبة 30.56%.
كم عدد الطرق المختلفة للحصول على 3 آحاد باستخدام 6 نرد؟

Jamie من Croydon, England

أولاً، هناك دالة الجمع (6، 3) = 20 طريقة لاختيار ثلاثة أحجار نرد من أصل 6 للحصول على الرقم واحد. ثم يمكن أن يكون كل رقم من الأرقام الثلاثة الأخرى أيًا من خمسة أرقام. إذن، مجموع الطرق هو 20 × 5 = 3 = 2500. إجمالي عدد طرق رمي جميع أحجار النرد هو 6 = 46656، لذا فإن احتمال الحصول على ثلاثة أرقام واحدة فقط هو 2500/46656 = 0.0536. للحصول على مساعدة في دالة الجمع، راجع قسم الاحتمالات في البوكر .
ما هو احتمال ظهور نتيجة واحدة على حجر نرد واحد عند رمي ثلاثة أحجار نرد معًا؟ حسب فهمي، يجب أن تكون النسبة ٥٠٪ (١/٦ + ١/٦ + ١/٦ = ١/٢ --> ٥٠٪)، ولكن في جدول الاحتمالات الخاص بك، كانت النسبة ٣٤.٧٢٪. أرجو المساعدة.

John C. من Singapore

احتمال الحصول على الرقم واحد فقط بثلاثة أحجار نرد هو 3*(5/6) 2 *(1/6) = 75/216 = 34.72%.
ما هو احتمال ظهور "زوج" عند رمي 4 أحجار نرد؟

Anthony من Toronto, Canada

يمكن أن يكون الزوج أي رقم من ستة أرقام. يمكن أن يكون الرقمان المنفردان الآخران من بين الأرقام الخمسة الأخرى. إذن، لدينا 6 × مجموعة (5، 2) = 60 تركيبة. لدينا مجموعة (4، 2) = 6 تركيبات من النرد يمكن أن يظهر عليها الزوج. يمكن ترتيب الرقمين المنفردين بطريقتين. إذن، لدينا 60 × 12 = 720 طريقة لرمي زوج. العدد الإجمالي لجميع طرق رمي النرد هو 6 × 4 = 1296. لذا، فإن الاحتمال هو 720/1296 = ~ 55.56%.
صديقي يملك بارًا، ولديه "ميلك شيك اليوم" حيث توجد عشرة أحجار نرد في وعاء بلاستيكي. ما احتمال مطابقة 8 من 10 في ميلك شيك واحد؟ شكرًا لوقتك.

August من Oshkosh, USA

احتمال رمي ١٠ أحجار نرد وتطابق ٨ أرقام بالضبط هو ٦*combin(١٠,٨)*(١/٦) ٨ *(٥/٦) ٢ = ١/٨٩٥٧.٩٥٢. احتمال مطابقة ٨ أرقام على الأقل هو ٦*[combin(١٠,٨)*(١/٦) ٨ *(٥/٦) ٢ + combin(١٠,٩)*(١/٦) ٩ *(٥/٦) + (١/٦) ١٠ ] = ١/٨٥٦٩.٤٦٩.
لقد رميتُ مؤخرًا، خلال لعبة طاولة زهر، رقمًا مزدوجًا ستة أربع مرات متتالية. ما احتمالات تكرار ذلك؟

David من Sunland, USA

مع كل لفة جديدة، احتمال أن تكون اللفات الأربع التالية كلها ستة مزدوجة هو (1/36) 4 = 1 في 1679616.
ما هو احتمال الحصول على ستريت برمية واحدة لخمسة نرد؟

Teodoro C. Deocares من Dagupan, Philippines

هناك نطاقان محتملان: من ١ إلى ٥ ومن ٢ إلى ٦. يمكن ترتيب كلٍّ من هذين النطاقين بـ ٥ طرق = ١٢٠ طريقة. هناك ٦ طرق = ٥ = ٧٧٧٦ طريقة لرمي خمسة أحجار نرد. لذا، فإن الاحتمال هو ٢ × ١٢٠ / ٧٧٧٦ = ٣.٠٩٪. يبدو أن هذا الاحتمال أعلى بكثير بعد أن وضعتُ العلامة ٠ للسلسلة الكبيرة أثناء لعبة ياهتز.
رُمي حجر نرد ذي وجهين ٣٠ مرة. ما هو العدد المتوقع لظهور الرقم ١؟ ما هو احتمال ظهور الرقم ١ في العدد المتوقع؟

مجهول

العدد المتوقع من الآحاد هو 30*(1/6) = 5. احتمال الحصول على 5 آحاد بالضبط هو combin(30,5)*(1/6) 5 *(5/6) 25 = 19.21%.
إذا كان لدي أي عدد من النرد، ما هو احتمال أنه إذا قمت برميها كلها، فإن واحدة على الأقل ستسقط على الرقم واحد؟

مجهول

احتمال ألا تكون جميع أحجار النرد واحدًا هو (5/6) n . لذا، فإن احتمال ظهور رقم واحد على الأقل هو 1-(5/6) n . لنأخذ مثالًا لخمسة أحجار نرد. الإجابة هي 1-(5/6) 5 = 59.81%.
إذا قمت برمي 36 نردًا، ما هو احتمال الحصول على ستة واحدة على الأقل؟

مجهول

1-(5/6) 36 = 99.86%
إذا واصلت الرمي وأزلت كل الستة في كل مرة، فكيف يمكنني التنبؤ بالعدد النظري للنرد المتبقي بعد عدد معين من الرميات؟

مجهول

في كل رمية، يُتوقع بقاء 5/6 من النرد. لذا، فإن العدد المتوقع للنرد المتبقي بعد n رمية هو 36*(5/6) n . على سبيل المثال، بعد 10 رميات، يتبقى لديك 5.81 نرد، في المتوسط.
إذا قمت برمي ثلاثة أحجار نرد، ما هو احتمال الحصول على رقمين متماثلين على الأقل؟

مجهول

احتمال اختلاف جميع الأرقام هو (5/6)*(4/6)=20/36. لذا، احتمال تطابق رقمين على الأقل هو 1-(20/36) = 16/36 = 44.44%.
إذا رمى شخصان نردًا، فما احتمال أن يكون العدد نفسه؟ هل هناك صيغة لحساب ذلك؟

مجهول

نعم. ببساطة، احسب مجموع الأرقام من ٢ إلى ١٢، ثم حدد احتمال ظهور كل رقم مرتين. ستكون الإجابة (١/٣٦) ٢ + (٢/٣٦) ٢ + (٣/٣٦) ٢ + (٤/٣٦) ٢ + (٥/٣٦) ٢ + (٦/٣٦) ٢ + (٥/٣٦) ٢ + (٤/٣٦) ٢ + (٣/٣٦) ٢ + (٢/٣٦) ٢ + (١/٣٦) ٢ = ١١٫٢٧٪.
حضرتُ مؤخرًا حفلًا في مستشفى. كانت هناك جائزة سيارة جديدة إذا نتج عن رمية واحدة ٧ نردات ٧ سداسيات. سعر الرمية الواحدة جنيه إسترليني واحد. احتمالات الفوز مرتفعة، ولكن ما مدى ارتفاعها؟

مجهول

احتمال ظهور سبعة أرقام ستاتية بسبعة نرد هو (1/6) 7 = 1 من 279,936. لذا، يجب أن تكون قيمة السيارة 279,936 جنيهًا إسترلينيًا أو أكثر ليكون هذا رهانًا جيدًا. حتى سيارة رولز رويس العادية لا تساوي هذا المبلغ، لذا أعتقد أن هذا رهان سيئ.

[يضيف بلو جاي: أجل، لكن أعتقد أن المغزى كان أنه كان للأعمال الخيرية. ما هو الأكثر متعة: التبرع بجنيه إسترليني واحد للأعمال الخيرية دون الحصول على أي شيء سوى الشعور الجميل بالمساعدة، أم التبرع بجنيه إسترليني واحد والحصول على شعور جيد بالإضافة إلى فرصة ضئيلة للفوز بسيارة؟]

ما هي احتمالات الحصول على 5 متماثلة، أو 4 متماثلة، أو 3 متماثلة، أو فول هاوس، أو زوجين، أو زوج، أو ستريت، أو لا شيء عند رمي خمسة نرد؟

مجهول

  • خمسة من نفس النوع: 6/6 5 = 0.08% (واضح)
  • أربعة من نفس النوع: 5*6*5 = 1.93% (خمسة مواضع ممكنة للبطاقة المفردة * 6 مراتب للبطاقة المفردة * 5 مراتب للبطاقة المفردة).
  • الفول هاوس: combin(5,3)*6*5/6 5 = 3.86% (combin(5,3) موضعًا للثلاثي المتماثل * 6 مراتب للثلاثي المتماثل * 2 مرتبة للزوج).
  • ثلاثة من نفس النوع: COMBIN(5,3)*COMBIN(2,1)*6*COMBIN(5,2) / 6 5 = 15.43%. (combin(5,3) موضعًا للثلاثة من نفس النوع * combin(2,1) موضعًا للأكبر من العناصر الفردية * 6 مراتب للثلاثة من نفس النوع * combin(5,2) مرتبة للعنصرين الفرديين.
  • زوجان: COMBIN(5,2)*COMBIN(3,2)*COMBIN(6,2)*4 / 6 5 = 23.15% (combin(5,2) موضع للزوج الأعلى * combin(3,2) موضع للزوج الأدنى * combin(6,4) مرتبة للزوجين * 4 مرتبة للعنصر المفرد.
  • الزوج: COMBIN(5,2)*fact(3)*6*combin(5,3) / 6 5 = 46.30% (combin(5,2) موضع للزوج * fact(3) موضع للعناصر الفردية الثلاثة * 6 مراتب للزوج * combin(5,3) مرتبة للعناصر الفردية.
  • مستقيم: 2*fact(5) / 6 5 = 3.09% (2 مدى للطرق المستقيمة {1-5 أو 2-6} * fact(5) لترتيب الطلب).
  • لا شيء: ((COMBIN(6,5)-2)*FACT(5)) / 6 5 = 6.17% (combin(6,5) طرق لاختيار 5 رتب من أصل ستة، ناقص 2 للمستقيمات، * fact(5) طرق لترتيب الترتيب.
مرحباً يا ساحر، أردتُ معرفة إن كان بإمكانك الإجابة على هذا السؤال. في لعبة قمار شهيرة في فرنسا في القرن السابع عشر، كان اللاعب يرمي نرداً ٢٤ مرة. يفوز برهانه إذا كانت إحدى هذه الرميات على الأقل رقم ستة مزدوج. كان هناك جدلٌ آنذاك حول ما إذا كان احتمال الفوز أعلى أم أقل من ٥٠٪. هل يمكنك مساعدتي؟

مجهول

بالتأكيد، هذا سهل. احتمال ظهور رقم ١٢ مرة واحدة على الأقل في ٢٤ رمية هو ١-(٣٥/٣٦) ٢٤ = ٤٩.١٤٪. لذا، فإن الاحتمالات ترجح المراهنة ضد الرقم ١٢. هذا رهان ذكي لأن العدد المتوقع لأرقام ١٢ في ٢٤ رمية هو ٢/٣. مع ذلك، هذا لا يعني أن احتمال ظهور الرقم ١٢ هو ٢/٣، لأنه في بعض الأحيان قد يكون هناك أكثر من رقم ١٢ واحد، واللاعب الذي يراهن على الرقم ١٢ لا يفوز بأي أرقام ١٢ إضافية بعد الرمية الأولى. إذا كان احتمال الفوز في أي محاولة هو ص، وعدد المحاولات هو ن، واحتمال الفوز مرة واحدة على الأقل هو و، فإن حل قيمة n بدلالة ص و و يعطينا...

w=1-(1-p) n
1-w = (1-p) n
log(1-w) = log((1-p) n )
log(1-w) = n*log(1-p)
n= log(1-w)/log(1-p)

في مثالنا، n = log(1-.5) / log(1-(1/36)) = log(0.5) / log(35/36) = 24.6051. لذا، إذا كانت احتمالية النجاح 50% في 24.6 رمية، فيجب أن تكون أقل قليلاً في 24 رمية.

ما هو احتمال الحصول على 1،2،3،4،5،6 باستخدام ستة أحجار نرد، ست مرات على التوالي؟

مجهول

يمكن التعبير عن احتمالية الحصول على العدد ١٢٣٤٥٦ بستة أحجار نرد في رمية واحدة على النحو التالي: احتمال (عدم تطابق النرد الثاني مع النرد الأول) * احتمال (عدم تطابق النرد الثالث مع النرد الأول أو الثاني) * ... = ١*(٥/٦)*(٤/٦)*(٣/٦)*(٢/٦)*(١/٦) = ٠٫٠١٥٤٣٢. وبالتالي، فإن احتمالية حدوث ذلك ست مرات متتالية هي ٠٫٠١٥٤٣٢. ٦ = ١ في ٧٤٫٠٣٧٫٢٠٨٫٤١١.
إذا قمت برمي حجر نرد واحد 6 مرات، ما هو احتمال الحصول على "2" 4 مرات بالضبط؟

مجهول

الجمع (6،2) * (1/6) 4 * (5/6) 2 = 0.008037551.
ما هو احتمال الحصول على 13 أو أكثر باستخدام 3 و4 و5 أحجار نرد، إذا سُمح لك بالاحتفاظ بأعلى ثلاثة أحجار نرد في رميتك؟

مجهول

وهنا الاحتمالات:

3 نرد: 25.93%
4 نرد: 48.77%
5 نرد: 66.13%.

لنفترض أننا ألقينا ثلاثة أحجار نرد عادية سداسية الأوجه. ما هو الاحتمال الشرطي أن يظهر النرد الأول العدد 4، علمًا بأن مجموع الأرقام الثلاثة الظاهرة هو 12؟

Shikha من North Ryde

احتمالية الحصول على A مع B هي احتمالية الحصول على A وB مقسومة على احتمالية الحصول على B. في هذه الحالة، احتمالية الحصول على 4 عند رمي النرد الأول، ثم الحصول على 8 عند رمي النردين الآخرين هي (1/6)*(5/36) = 5/216. احتمالية الحصول على 12 عند رمي 3 نرد هي 25/216، كما هو موضح في قسم لعبة sic bo . لذا، الإجابة هي (5/216)/(25/216) = 5/25 = 20%.
في تمرين برمجة حديث، طُلب مني ومن طلاب آخرين وصف حجر نرد سداسي الأوجه باستخدام الكود، ثم استخدام حجر النرد لتحديد طريقة لعب لعبة بسيطة. كان هدف اللعبة رمي النرد حتى يصل مجموع الرميات إلى 100 بالضبط. أي رمية تزيد المجموع عن 100 لن تُضاف، بل تُضاف فقط إلى الإحصائيات. وسرعان ما حُدد أن 17 رمية هي أقل عدد من الرميات اللازمة للوصول إلى 100. إلا أن حساب احتمالات حدوث ذلك كان صعب المنال. فحساب احتمالات تسلسل معين من الرميات أمر بسيط، ولكن كيف يُمكن للمرء أن يأخذ في الاعتبار الترتيب غير المحدد للرميات، والطرق المختلفة للوصول إلى 100 في 17 رمية (16*6 + 1*4 و15*6 + 2*5)؟

Björn من Göteborg, Sweden

الطريقتان اللتان ذكرتهما هما الطريقتان الوحيدتان للحصول على إجمالي ١٠٠ في ١٧ رمية. احتمال الحصول على ١٦ سداسية وواحدة من الأربع هو ١٧*(١/٦) ١٧. يوجد ١٧ موضعًا محتملًا للرقم ٤، ولكل متتالية احتمال (١/٦)*(١/٦)*...*(١/٦) مع ١٧ حدًا. عدد طرق الحصول على ١٥ سداسية و٢ خماسيتين هو الجمع (١٧، ٢) = ١٣٦. لذا، فإن احتمال الحصول على ١٥ سداسية و٢ خماسيتين هو ١٣٦*(١/٦) ١٧. لذا، فإن الاحتمال الإجمالي هو (١٧+١٣٦)*(١/٦) ١٧ = ١ في ١١٠,٦٣١,٧٦١,٠٧٧.
هناك ثلاثة أحجار نرد، اثنان منها سداسي الأوجه، وواحد نرد جميع أوجهه تحتوي على الرقم ستة. جميع النردات في جيبي. أخرجتُ نردًا عشوائيًا ورميته. النتيجة ٦. ما احتمال أن يكون النرد أحد النردات الصحيحة بستة قيم مختلفة؟

Annojh من Toronto

دع A = اختيار النرد الطبيعي
دع B = رمي الرقم 6 باستخدام نرد تم اختياره عشوائيًا
الإجابة = Pr(A معطاة B) = Pr(A وB)/pr(B) = ((2/3)*(1/6))/((2/3)*(1/6)+(1/3)*1) = (2/18)/((2/18)+(6/18)) = 1/4.
إذا كان بإمكانك رمي ستة نرد مرة واحدة فقط، ما هو احتمال رمي 6،6،6،6،1، و4 بأي ترتيب؟

Aubrey من Kokomo

هناك 6!/(4!*1!*1!) = 30 طريقة لترتيب هذه الأعداد بأي ترتيب. وبعبارة أخرى، هناك 6 مواضع لوضع الرقم 1، و5 مواضع متبقية لوضع الرقم 4، لذا 6*5 = 30. احتمال الحصول على العدد 666614 بهذا الترتيب بالضبط هو 1 من 6 = 1 من 46656. اضرب هذا في 30 للترتيبات الثلاثين المحتملة، والإجابة هي 30/46656 = 0.0643%، أو 1 من 1552.2.
أفهم أن "وقت الانتظار" لحدث ما هو مقلوب احتمال وقوعه. أرغب في حساب وقت الانتظار للحصول على رقم 2 متتالي باستخدام حجر نرد واحد. في محاكاة، أحصل على 42 رمية في المتوسط. كيف أربط ذلك باحتمال الحصول على رقم 2 متتالي؟

Lee من Andover

صحيح أنه في حالة الأحداث الفردية، إذا كان الاحتمال p، فإن متوسط وقت الانتظار هو 1/p. لكن الأمر يزداد تعقيدًا مع الأحداث المتتالية. لنفترض أن x هي الحالة التي لم تكن فيها آخر رمية 2. هذه هي الحالة أيضًا في البداية. لنفترض أن y هي الحالة التي كانت فيها آخر رمية 2. بعد الرمية الأولى، هناك احتمال 5/6 أن نبقى في الحالة x، واحتمال 1/6 أن نكون في الحالة y. لنفترض أن Ex(x) هو العدد المتوقع للرميات من الحالة x، وأن Ex(y) هو العدد المتوقع من الحالة y. إذًا...

Ex(x) = 1 + (5/6)*ex(x) + (1/6)*ex(y)، و
Ex(y) = 1 + (5/6)*ex(x)

حل هاتين المعادلتين...

Ex(x) = 1 + (5/6)*ex(x) + (1/6)*( 1 + (5/6)*Ex(x))
Ex(x) = 7/6 + (35/36)*Ex(x)
(1/36)*Ex(x) = 7/6
Ex(x) = 36*(7/6) = 42

وبالتالي فإن متوسط وقت الانتظار للحصول على اثنين متتاليين هو 42 لفة.

لدي نفس النوع من المشكلة، فقط من المتوقع أن تحصل على رأسين، في موقعي لمشاكل الرياضيات ، انظر المشكلة 128.

هل يمكنك إخباري باحتمالات رمي رقمين متطابقين باستخدام حجري نرد، أو ثلاثة، أو أربعة؟ أتساءل عن عدد أحجار النرد التي يجب رميها في المرة الواحدة لتكون الاحتمالات لصالح الشخص الذي يرمي النرد. (لا يهم أي رقم مضاعف).

Mary من Minneapolis, MN

إليك احتمالية الحصول على رقم واحد على الأقل أكثر من مرة وفقًا لعدد اللفات:

احتمال وجود زوج أو أكثر

لفات احتمال
2 لفافة 16.67%
3 لفات 44.44%
4 لفات 72.22%
5 لفات 90.74%
6 لفات 98.46%

لذا إذا كنت تريد حجز هذا، يجب عليك تقديم "نعم" مع 3 لفات أو "لا" مع 4 لفات.
ما احتمال الحصول على مجموع أكبر من ١٠٠ عند رمي ٢٠ نردًا؟ مع تحياتي.

Terje من Stockholm

بدأتُ باستخدام التقريب الطبيعي لحل هذه المسألة، لكن احتمالية تجاوز 100 نقطة منخفضة جدًا بحيث لا تكون هذه الطريقة دقيقة. لذلك، أجريتُ محاكاة عشوائية لـ 8.25 مليون تجربة، وكان عدد التجارب التي بلغت 101 نقطة أو أكثر 127. لذا، فإن الاحتمالية هي حوالي 1 من 65,000.
يا ساحر، هل يمكنك من فضلك وصف احتمالات الفوز في كاليفورنيا سوبر لوتو بلس (1 من 41.4 مليون)، من حيث عدد مرات رمي الرقم 7 أو 11 المتتالية؟ سمعتُ ذلك من قبل. معظم الناس لا يفهمون احتمالات اليانصيب. لكن رمي النرد... يفهمونه.

Tim من Belmont, CA

لتكن إجابتك n. احتمال ظهور ٧ أو ١١ هو ٨/٣٦. لإيجاد قيمة n:

(8/36) ن = 1/41,400,000

log((8/36) n ) = log(1/41,400,000)

n × log(8/36) = log(1/41,400,000)

n = log(1/41,400,000)/log(8/36)

ن = -7.617 / -0.65321

ن = 11.6608

إذن، احتمال الفوز في اليانصيب الكبير يساوي رمي الرقم سبعة أو أحد عشر 11.66 مرة متتالية. ولمن لا يفهمون الرمية الجزئية، أقول إن الاحتمال يقع بين 11 و12 رمية متتالية.

نحن في خلاف بين العمال. يوجد حانة في نهاية الشارع تُقدم شيكًا يوميًا. وهو أن ترمي خمسة أحجار نرد دفعة واحدة، ويجب أن تكون جميعها متشابهة "مثل لعبة الياهتز"، لكنه يمنحك ثلاث فرص. لكن يجب عليك التقاط جميع النرد ثلاث مرات. إذًا، السؤال هو: ما هي احتمالات تكرار الشيك في شيك واحد؟ وما هي احتمالات تكراره في الشيك الثلاث المسموح بها؟ شكرًا، إذا أجبت على هذا السؤال من قبل، فأنا آسف، لكنني لم أتمكن من العثور عليه.

Dan and co workers at maple island من Forest Lake

احتمال ظهور خمسة نردات متشابهة في رمية واحدة هو 6 × (1/6) 5 = 1/1296. هذا لأن هناك ستة نردات متشابهة (واحد إلى ستة)، واحتمال ظهور هذا العدد في كل نرد هو (1/6). احتمال عدم ظهور خمسة نردات متشابهة هو 1-(1/1296) = 1295/1296. احتمال عدم ظهور ثلاثة نردات متشابهة في ثلاث محاولات هو (1295/1296) 3 = 99.77%. لذا، فإن احتمال ظهور نرد واحد على الأقل من خمسة نردات متشابهة في ثلاث محاولات هو 100% - 99.77% = 0.23%.
ما هو العدد المتوقع من الرميات المطلوبة للحصول على نتيجة واحدة على الأقل من كل نتيجة ممكنة على حجر نرد غير متحيز ذي 6 أوجه؟

Michael من Melbourne

إذا كان احتمال حدوث شيء ما هو ص، فسيستغرق حدوثه في المتوسط 1/ص من المحاولات الأولى. من البديهي أنك ستشطب رقمًا واحدًا في الرمية الأولى. أما احتمال ظهور أحد الأرقام الخمسة الأخرى بعد ذلك فهو 5/6. لذا، سيستغرق حدوث ذلك في المتوسط 1/(5/6) = 6/5 = 1.2 رمية. باتباع هذا المنطق حتى النهاية، فإن عدد الرميات المتوقع هو (6/6) + (6/5) + (6/4) + (6/3) + (6/2) + (6/1) = 14.7.
ما هو الاحتمال الكلاسيكي للحصول على مجموع 12 عند رمي 5 نرد متوازنة؟

Kennith H. من Winters

أتمنى أن تكون سعيدًا، لقد أضفتُ قسمًا جديدًا يُجيب على أسئلة كهذه لأسئلة تتراوح من 1 إلى 25 حجر نرد. وكما يُظهر جدول النردات الخمسة، فإن احتمال الحصول على 12 هو 0.039223251028807.

إذا تم رمي نردين مرارًا وتكرارًا، حتى يحدث أي من الحدثين التاليين، فأيهما من المرجح أن يحدث أولاً:

  • يتم الحصول على مجموع ستة وثمانية، بأي ترتيب، مع السماح بالتكرارات.
  • يتم الحصول على العدد سبعة مرتين.

راهنني أحدهم على أن الرقمين ستة وثمانية سيظهران أولاً. قبلتُ الرهان لأن الرقم سبعة هو الأرجح. مع ذلك، خسرتُ ٢٥٠٠ دولار بسبب تكرار هذا الأمر. ما هي احتمالات ذلك؟

Anthony من Indiana

أخشى أنك راهنت على الجانب المربع. احتمال ظهور رقمي سبعة قبل ستة وثمانية هو ٤٥٫٤٤٪. إليك جميع النتائج المحتملة. العمود الأول هو ترتيب رميات النرد المحتملة لنتيجة الرهان، مع تجاهل جميع الاحتمالات الأخرى.

رهان سبعتين قبل ستة وثمانية

لفات ذات صلة احتمال صيغة حصيلة
6,8 0.142045 (16/5)*(11/5) يخسر
8,6 0.142045 (16/5)*(11/5) يخسر
6،7،8 0.077479 (16/5)*(11/6)*(11/5) يخسر
7،6،8 0.053267 (16/6)*(16/5)*(11/5) يخسر
8،7،6 0.077479 (16/5)*(11/6)*(11/5) يخسر
7،8،6 0.053267 (16/6)*(16/5)*(11/5) يخسر
7,7 0.140625 (16/6)*(16/6) يفوز
6،7،7 0.092975 (16/5)*(11/6)*(11/6) يفوز
8،7،7 0.092975 (16/5)*(11/6)*(11/6) يفوز
7،6،7 0.06392 (16/6)*(16/5)*(11/6) يفوز
7،8،7 0.06392 (16/6)*(16/5)*(11/6) يفوز

في الأساس، السبب في أن 6 و8 هما الجانب الأفضل هو أنه يمكنك ضرب هذه الأرقام بأي ترتيب: 6 ثم 8، أو 8 ثم 6. مع وجود سبعتين، هناك ترتيب واحد فقط، 7 ثم 7 آخر.

سؤالان من فضلكم: ١) ما احتمال ظهور ٦، ٦، ٦، ٦، ٦، ٦ مرة واحدة باستخدام حجر نرد ذي ستة أوجه؟ ٢) ما احتمال ظهور ١، ٢، ٣، ٤، ٥، ٦ مرة واحدة باستخدام حجر نرد ذي ستة أوجه؟ شكرًا! هذا يُرهقني!

Heather من Petaluma

احتمال الحصول على ستة سداسيات هو (1/6) 6 = 1 في 46656. احتمال الحصول على 1،2،3،4،5،6 بستة أحجار نرد هو 6 ! /6 6 = 1 في 64.8
ما هو احتمال الحصول على أي رقم معين أكثر من مرة إذا قمت برمي النرد عشر مرات؟

Ryan من Silay

1-(5/6) 10 -10 × (1/6) × (5/6) 9 = 51.55%.
في لعبة تُسمى "الضرائب والتهرب الضريبي"، يرمي اللاعب زوجًا من النرد. في أي رمية، إذا كان المجموع ٧ أو ١١ أو ١٢، يُحاسب اللاعب؛ أما في أي رمية أخرى، فيتجنب الضرائب. إذا رمى اللاعب زوج النرد ٥ مرات، فما احتمال تهربه من الضرائب؟

George P. من Stevens Point, WI

احتمال ظهور ٧، ١١، أو ١٢ هو (٦ + ٢ + ١) / ٣٦ = ٩/٣٦ = ١/٤. راجع قسمي حول أساسيات احتمالات النرد لمعرفة كيفية التوصل إلى هذا الرقم. احتمال ظهور أي نتيجة أخرى هو ٣/٤. احتمال تكرار خمس رميات دون ظهور ٧، ١١، أو ١٢ هو (٣/٤) ٥ = ٢٣.٧٣٪.
كم عدد رميات النرد اللازمة قبل أن يُرجَّح أنك رميت الأرقام ١، ٢، ٣، ٤، ٥، و٦ مرة واحدة على الأقل في كل مرة؟ هل لديكم أي أفكار لتعميم هذا على نرد ذي n وجه؟

Asif من Columbia, SC

ليس أنك سألت، ولكن دعني أتناول المتوسط الحسابي أولًا. لنرد ذي ستة أوجه، العدد المتوقع للرميات للحصول على كل وجه مرة واحدة على الأقل هو (6/6)+(6/5)+(6/4)+(6/3)+(6/2)+(6/1) = 14.7. لنرد ذي n وجه، العدد المتوقع للرميات هو (n/n) + (n/(n-1)) + (n/(n-2)) + ... + n. متوسط عدد الرميات المطلوبة هو 13. احتمال الحصول على 13 رمية أو أقل هو 51.4%، واحتمال الحصول على 13 رمية أو أكثر هو 56.21%.
أعلم أنك متشكك في التحكم بالنرد. لقد كنت أتدرب على ضبط النرد والتحكم في الرمي لمدة ثلاثة أشهر. ما هو احتمال ظهور 78 رقمًا سبعةً من أصل 655 رمية عشوائيًا؟ شكرًا لمساعدتك :)

Eric B. من Boston, MA

بالنسبة لعدد كبير من الرميات، يُمكننا استخدام تقريب منحنى غاوس. العدد المتوقع للسبعات في 655 رمية هو 655 × (1/6) = 109.1667. التباين هو 655 × (1/6) × (5/6) = 90.9722. الانحراف المعياري هو sqr(90.9722) = 9.5379. عدد السبعات الـ 78 لديك أقل من المتوقع بمقدار 109.1667 − 78 = 31.1667. هذا يساوي (31.1667 - 0.5) / 9.5379 = 3.22 انحراف معياري عن المتوقع. احتمالية انخفاض 3.22 انحراف معياري أو أكثر عن المتوقع هي 0.000641، أو 1 من 1560. حصلت على هذا الرقم في Excel، باستخدام الصيغة normsdist(-3.22).
يتعلق هذا الأمر بالتحكم في النرد في لعبة الكرابس. سبق أن ناقشتَ تجربة ستانفورد وونغ ، وقلتَ: "كانت شروط الرهان هي ما إذا كان بإمكان الرماة الدقيقين رمي أقل من 79.5 رقم سبعة في 500 رمية. العدد المتوقع في لعبة عشوائية هو 83.33. احتمال رمي 79 رقم سبعة أو أقل في 500 رمية عشوائية هو 32.66%... واحتمال رمي 74 رقم سبعة أو أقل في 500 رمية عشوائية هو 14.41%."

السؤال الذي لدي بخصوص هذا الرهان هو أن 14.41% لا يزال غير "ذو دلالة إحصائية" [أي p < 0.05]، وهو ما يُفهم عادةً على أنه يعني أكبر من انحرافين معياريين عن المتوسط - أو احتمال أقل من 5% * مجتمعة* من وقوع الحدث عشوائيًا في أي من طرفي السلسلة.

كم عدد السبعات التي يجب أن تظهر في 500 لفة قبل أن تتمكن من القول أن هناك فرصة أقل من 2.5٪ أن النتيجة كانت عشوائية تمامًا (أي أن النتيجة كانت ذات دلالة إحصائية)؟

شكرا جزيلا وبالمناسبة، موقعك هو أفضل موقع على الإطلاق فيما يتعلق بموضوع احتمالات وفرص المقامرة التي وجدتها .... استمر في العمل الجيد !!!

Plexus من Warwick, Rhode Island

شكراً لكلماتك الطيبة. لا يجب أن تُصرّح بأن احتمالية عدم عشوائية الرميات هي p. بل يجب أن تُصاغ على أن احتمالية أن تُسفر لعبة عشوائية عن مثل هذه النتيجة هي p. لم يتوقع أحد أن تُثبت 500 رمية أي شيء أو تُدحضه. لم أكن أنا من حدد الخط عند 79.5 سبعات، لكنني أشك في أنه تم اختياره ليكون ذا دلالة إحصائية؛ بل أظن أنه كان نقطةً يتفق عندها الطرفان على الرهان.

مستوى الدلالة 2.5% يساوي 1.96 انحرافًا معياريًا عن التوقعات. يمكن حساب ذلك باستخدام الصيغة =normsinv(0.025) في برنامج إكسل. الانحراف المعياري لـ 500 رمية هو sqr(500*(1/6)*(5/6)) = 8.333. لذا، فإن 1.96 انحرافًا معياريًا يساوي 1.96 * 8.333 = 16.333 رمية أقل من التوقعات. العدد المتوقع للسبعات في 500 رمية هو 500*(1/6) = 83.333. لذا، فإن 1.96 انحرافًا معياريًا أقل من ذلك يساوي 83.333 − 16.333 = 67. وبالتحقق من ذلك باستخدام التوزيع الثنائي، فإن الاحتمال الدقيق لـ 67 أو أقل من السبعات هو 2.627%.

ما هو العدد المتوقع من اللفات اللازمة للحصول على ياتزيه؟

Ian F. من Provo

بافتراض أن اللاعب يحمل دائمًا الرقم الأكثر تمثيلًا، يكون المتوسط ١١٫٠٩. فيما يلي جدول يوضح توزيع عدد الرميات على محاكاة عشوائية لـ ٨٢٫٦ مليون محاولة.

تجربة ياتزي

لفات الحوادث احتمال
1 63908 0.00077371
2 977954 0.0118396
3 2758635 0.0333975
4 4504806 0.0545376
5 5776444 0.0699327
6 6491538 0.0785901
7 6727992 0.0814527
8 6601612 0.0799227
9 6246388 0.0756221
10 5741778 0.0695131
11 5174553 0.0626459
12 4591986 0.0555931
13 4022755 0.0487016
14 3492745 0.042285
15 3008766 0.0364257
16 2577969 0.0312103
17 2193272 0.0265529
18 1864107 0.0225679
19 1575763 0.019077
20 1329971 0.0161013
21 1118788 0.0135446
22 940519 0.0113864
23 791107 0.00957757
24 661672 0.00801056
25 554937 0.00671837
26 463901 0.00561624
27 387339 0.00468933
28 324079 0.00392347
29 271321 0.00328476
30 225978 0.00273581
31 189012 0.00228828
32 157709 0.00190931
33 131845 0.00159619
34 109592 0.00132678
35 91327 0.00110565
36 76216 0.00092271
37 63433 0.00076795
38 52786 0.00063906
39 44122 0.00053417
40 36785 0.00044534
41 30834 0.00037329
42 25494 0.00030864
43 21170 0.0002563
44 17767 0.0002151
45 14657 0.00017745
46 12410 0.00015024
47 10299 0.00012469
48 8666 0.00010492
49 7355 0.00008904
50 5901 0.00007144
51 5017 0.00006074
52 4227 0.00005117
53 3452 0.00004179
54 2888 0.00003496
55 2470 0.0000299
56 2012 0.00002436
57 1626 0.00001969
58 1391 0.00001684
59 1135 0.00001374
60 924 0.00001119
61 840 0.00001017
62 694 0.0000084
63 534 0.00000646
64 498 0.00000603
65 372 0.0000045
66 316 0.00000383
67 286 0.00000346
68 224 0.00000271
69 197 0.00000238
70 160 0.00000194
71 125 0.00000151
72 86 0.00000104
73 79 0.00000096
74 94 0.00000114
75 70 0.00000085
76 64 0.00000077
77 38 0.00000046
78 42 0.00000051
79 27 0.00000033
80 33 0.0000004
81 16 0.00000019
82 18 0.00000022
83 19 0.00000023
84 14 0.00000017
85 6 0.00000007
86 4 0.00000005
87 9 0.00000011
88 4 0.00000005
89 5 0.00000006
90 5 0.00000006
91 1 0.00000001
92 6 0.00000007
93 1 0.00000001
94 3 0.00000004
95 1 0.00000001
96 1 0.00000001
97 2 0.00000002
102 1 0.00000001
المجموع 82600000 1
لنفترض لعبة افتراضية تعتمد على رمي نرد. إذا استقر النرد على الرقم ١، يخسر اللاعب دولارًا واحدًا وتنتهي اللعبة. إذا استقر النرد على أي شيء آخر، يربح اللاعب دولارًا واحدًا. عند هذه النقطة، يمكن للاعب ترك الأمر كما هو أو الانسحاب. يمكن للاعب الاستمرار في اللعب، مع مضاعفة كل رهان، حتى يخسر أو ينسحب. ما هي أفضل استراتيجية؟

Byron P. من Newington, CT

من أجل تعظيم القيمة المتوقعة فقط، يجب على اللاعب اللعب للأبد. مع أن احتمال خسارة اللاعب في النهاية هو 1، إلا أن القيمة المتوقعة في أي نقطة قرار تُفضّل دائمًا إعادة اللعب. يبدو الأمر متناقضًا. يكمن الجواب في أن بعض الأحداث لها احتمال 1، ولكنها قد لا تحدث. على سبيل المثال، إذا رميت سهمًا على خط أعداد من 0 إلى 10، فإن احتمال عدم إصابة باي هو 1 تمامًا، ولكنه لا يزال واردًا.

مع ذلك، ولأغراض عملية، ثمة نقطة توقف. ذلك لأن السعادة التي يجلبها المال لا تتناسب طرديًا مع المبلغ. فبينما من المتعارف عليه أن زيادة المال تجلب سعادة أكبر، إلا أنه كلما ازداد ثراءك، قلّت سعادتك مع كل دولار إضافي.

أعتقد أن الحل الأمثل لهذا السؤال هو تطبيق معيار كيلي على المسألة. وفقًا لكيلي، على اللاعب اتخاذ كل قرار بهدف تعظيم اللوغاريتم المتوقع لرصيده بعد الرهان. ولاختصار هذا (لقد حذفتُ الكثير من الحسابات)، يجب على اللاعب الاستمرار في مضاعفة رهانه حتى يتجاوز 96.5948% من إجمالي ثروته. تُعرّف الثروة بأنها مجموع المبلغ الذي ربحه بالإضافة إلى أي مبلغ كان يملكه اللاعب قبل وضع رهانه الأول. على سبيل المثال، إذا كان لدى اللاعب 100,000 دولار أمريكي في البداية، فعليه الاستمرار في مضاعفة الرهان حتى 23 مرة، ليصل إلى ربح قدره 4,194,304 دولارات أمريكية. عندها، ستكون ثروة اللاعب الإجمالية 4,294,304 دولارات أمريكية. وسوف يُطلب منه المراهنة بمبلغ 4,194,304/4,294,304 = 96.67% من إجمالي ثروته، وهو أكبر من نقطة التوقف 96.5948%، لذا يجب عليه التوقف.

يرمي اللاعبان أ و ب زوجًا من النرد. يفوز اللاعب أ إذا رمى بمجموع 6 قبل أن يرمي ب مجموع 7، ويفوز ب إذا رمى بمجموع 7 قبل أن يرمي أ 6. إذا بدأ أ، فأظهر أن فرص فوز أ هي 30/61.

Sangeeta من Mumbai, India

لنفترض أن إجابة هذا السؤال هي p. احتمال ظهور ستة هو ٥/٣٦، واحتمال ظهور سبعة هو ٦/٣٦. إذا لم تفهم السبب، يُرجى مراجعة قسمي حول أساسيات احتمالات النرد . يمكننا تعريف p على النحو التالي:

p = احتمال (6 في اللفة الأولى) + احتمال (لا يوجد 6 في اللفة الأولى) * احتمال (لا يوجد 7 في اللفة الثانية) * p.

يرجع ذلك إلى أنه إذا لم يفوز أي لاعب بعد الرميتين الأوليين، تعود اللعبة إلى حالتها الأصلية، ويظل احتمال فوز اللاعب أ كما هو.

إذن لدينا:

ص = (5/36) + (31/36)×(30/36)×ص
ص = 5/36 + (930/1296)×ص
ص * (1-(930/1296)) = 5/36.
ص * (366/1296) = 5/36
ص = (5/36)×(1296/366) = 30/61.

كم عدد الطرق المتاحة لرمي نرد ذي ستة أوجه غير متمايزة؟ كما ذكرنا، النرد غير متمايز، لذا، مع خمسة نرد مثلاً، تُعتبر النتائج 1-1-3-5-6 و1-6-5-1-3 هي نفس النتيجة. مع نردين، من السهل تحديد أن الإجابة هي 21، لكنني لا أستطيع إيجاد حل شامل ودقيق.

Don من New York

يمكن التعبير عن الإجابة بالصيغة combin(n+5,n) = (n+5)!/(120×n!). إليك الإجابة لعدد من أحجار النرد يتراوح بين 1 و20 حجر نرد.

مجموعات النرد غير المميزة

النرد التركيبات
1 6
2 21
3 56
4 126
5 252
6 462
7 792
8 1287
9 2002
10 3003
11 4368
12 6188
13 8568
14 11628
15 15504
16 20349
17 26334
18 33649
19 42504
20 53130
21 65780
22 80730
23 98280

يعود الفضل إلى آلان تاكر، مؤلف كتاب التركيبات التطبيقية .

هل يمكنك حساب احتمال ظهور رقمين متتاليين في رمية النرد؟ بمعنى آخر، ما هو احتمال ظهور رقمين 4 أو 6 أو 7 متتاليين؟ أُدرك أن الماضي لا يُمكنه التنبؤ بالمستقبل، ولكن هل هناك طريقة لحساب حاصل ضرب 7/36 × 7/36 متتاليين؟ آمل أن يكون هذا منطقيًا.

James من Birmingham

بالتأكيد. هذا سيكون Pr(2) 2 + Pr(3) 2 + ... + Pr(12) 2 = (1/36) 2 + (2/36) 2 + (3/36) 2 + (4/36) 2 + (5/36) 2 + (6/36) 2 + (5/36) 2 + (4/36) 2 + (3/36) 2 + (2/36) 2 + (1/36) 2 = 11.27%.
في 180 رمية متتالية للنرد، كم مرة يمكنني أن أتوقع رؤية ما يلي:

سبعتان على التوالي؟
ثلاث سبعات على التوالي؟
أربع سبعات على التوالي؟

شكرا على وقتك :-).

Melanie D. من Elizabeth City, NC

لا أستطيع أن أفكر في أي سبب مفيد لمعرفة هذه المعلومات، ولكن يُطرح عليّ هذا النوع من الأسئلة كثيرًا، لذا سأجيبك.

من الأسهل قليلاً الحصول على سلسلة محددة من السبعات تبدأ بالرمية الأولى أو تنتهي بالرمية الأخيرة، لأن السلسلة محدودة من جانب واحد. على وجه التحديد، احتمال الحصول على سلسلة من s من السبعات، تبدأ بالرمية الأولى أو تنتهي بالأخيرة، هو (1/6) س × (5/6). الحد 5/6 هو لأنه يجب الحصول على رقم غير 7 في النهاية المفتوحة للسلسلة.

احتمال بدء سلسلة من s سبعة في أي نقطة في منتصف السلسلة هو (1/6) s × (5/6) 2 . نقوم بتربيع الحد 5/6، لأنه يجب على اللاعب الحصول على رقم غير 7 في كلا طرفي السلسلة.

إذا كان هناك r رمية، فسيكون هناك خانتان للتسلسل الداخلي، وrn-1 خانة لسلسلة من n سبعات. بوضع هذه المعادلات في جدول، إليك العدد المتوقع لتسلسلات السبعات، من 1 إلى 10. العمود "الداخلي" هو 2*(5/6)*(1/6) r ، والعمود "الخارجي" هو (179-r)*(5/6) 2 *(1/6) r ، حيث r هو عدد السبعات في السلسلة. لذا، يمكننا توقع 3.46 رمية من سبعتين، و0.57 رمية من ثلاث سبعات، و0.10 رمية من أربع سبعات.

المتوقع تشغيل السبعات في 180 لفة

يجري داخل الخارج المجموع
1 0.277778 20.601852 20.87963
2 0.046296 3.414352 3.460648
3 0.007716 0.565844 0.57356
4 0.001286 0.093771 0.095057
5 0.000214 0.015539 0.015754
6 0.000036 0.002575 0.002611
7 0.000006 0.000427 0.000433
8 0.000001 0.000071 0.000072
9 0 0.000012 0.000012
10 0 0.000002 0.000002
يتم رمي حجري نرد حتى يصبح المجموع 12 أو مجموعين متتاليين 7. ما هو احتمال أن يتم رمي الرقم 12 أولاً؟

مجهول

يمكن العثور على الإجابة والحل على موقعي المرافق، mathproblems.info ، المشكلة رقم 201.
أنا لاعب طاولة، وكنتُ أجري نقاشًا مع أصدقائي حول النرد الصلب الأفلاطوني غير المكعب (إذا كنتَ مهووسًا باللعبة، فهذا يعني d4 وd8 وd12 وd20). جادلوا بأن هذه هي النردات الوحيدة التي ستكون عادلة بشكل واضح. وجادلتُ بأن تصنيعها لتكون عادلة سيكون صعبًا للغاية. كما أن الألعاب الوحيدة المتاحة ستكون نسخًا مختلفة من لعبة الكرابس، والتي تُصبح مُرهقة للغاية بسبب عدد النتائج الإضافية. هل سبق لأي كازينو أن استخدم نردًا سداسي الأوجه غير تقليدي؟

Bayani من Carnagie, PA


هذه ليزا فورمان، عارضة الأزياء من مراجعتي لكازينو M. عندما حاولتُ إبهارها بالقول إن شكل البالون على اليسار هو مجسم عشروني الوجوه مقطوع ، ابتسمت فقط وقلبت عينيها.

لا تجرؤ على تحدي مؤهلاتي كخبير رياضيات! عندما كنت طالبًا في السنة الثانية من المرحلة الثانوية، لم أقم فقط ببناء جميع الأشكال الأفلاطونية باستخدام لوح ملصقات وشريط كهربائي، بل أيضًا جميع الأشكال الأرخميدية .

إذا اقتصرت على المضلعات المنتظمة، وأردت أن يكون لكل وجه نفس الاحتمال، فستقتصر على المجسمات الأفلاطونية. ومع ذلك، إذا استطعت رفع شرط المضلع المنتظم، فيمكنك إضافة المجسمات الكاتالونية الثلاثة عشر أيضًا.

للإجابة على سؤالك الآخر، لا، لم أرَ قط لعبةً في كازينو تستخدم نردًا غير المكعبات. قبل حوالي عشر سنوات، شاهدتُ لعبةً عُرضت في معرض ألعاب في أتلانتيك سيتي، أعتقد أنها استخدمت مجسمًا ثلاثي السطوح معينيًا ، وهو أحد الأشكال المجسمة الكاتالونية، لكنني لا أعتقد أنها عُرضت في كازينو قط. هناك لعبةٌ أراها عامًا بعد عام في معرض الألعاب العالمي تستخدم قمةً دوارة (مثل الدريدل)، لكن للأسف، لم أرَ ذلك في كازينو أيضًا.

إذا قمت برمي ثلاثة أحجار نرد ذات ستة أوجه، ما هي احتمالات الحصول على نتيجة متتالية، وأيضًا، ما هي احتمالات الحصول على نتيجة ثلاثة من نفس النوع؟

Mark من Fargo, ND

هناك 6 = 3 = 216 طريقة لرمي ثلاثة أحجار نرد. ست من هذه التركيبات ستؤدي إلى نتيجة ثلاثية متماثلة (1-1-1 إلى 6-6-6). لذا، فإن احتمال الحصول على نتيجة ثلاثية متماثلة هو 6/216 = 1/36. هناك أربع فترات زمنية ممكنة لرمية متتالية (1-2-3 إلى 4-5-6). كما توجد 3 = 6 طرق لترتيب النرد الثلاثة في متتالية. وبالتالي، هناك 4 × 6 = 24 تركيبة متتالية. وبالتالي، فإن احتمال الحصول على نتيجة متتالية هو 24/216 = 1/9.
ما هو متوسط الناتج عند رمي أربعة أحجار نرد سداسية الأوجه بعد طرح أقل نتيجة (المعروفة بـ 4d6-L)؟ ما هو الانحراف المعياري لهذه الرمية؟

Aaron من New York

يوضح الجدول التالي عدد التركيبات لجميع الإجماليات المحتملة من 3 إلى 18.

التركيبات في 4d6-L

حصيلة التركيبات
3 1
4 4
5 10
6 21
7 38
8 62
9 91
10 122
11 148
12 167
13 172
14 160
15 131
16 94
17 54
18 21
المجموع 1296

المتوسط الحسابي هو 12.2446، والانحراف المعياري هو 2.8468.

سؤالي مبني على احتمالات النرد. أعلم أن هناك ست طرق للحصول على ٧ وطريقة واحدة للحصول على ١٢، ولكن ما هي احتمالات الحصول على ست نقاط ٧ قبل نقطة ١٢ واحدة؟ هل هما زوجية، وإن لم يكونا كذلك، فكم عدد النقاط ١٢ التي يجب إضافتها إلى المعادلة لجعلها زوجية؟

nick

احتمال ظهور الرقم ٧ هو ١/٦، واحتمال ظهور الرقم ١٢ هو ١/٣٦. واحتمال ظهور الرقم ٧، إذا كانت الرمية ٧ أو ١٢، هو (١/٦)/((١/٦)+(١/٣٦)) = ٦/٧. لذا، فإن احتمال ظهور الرقم ٦ في أول ست مرات من الرميات، أي ٦ مرات، هو ( ٦/٧ ) = ٣٩.٦٦٪.

إذا أعدت صياغة السؤال ليكون: ما هو احتمال ظهور خمس نتائج 6 قبل ظهور 12؟ الإجابة هي (6/7) 5 = 46.27%. بأربع رميات، تكون النسبة (6/7) 4 = 53.98%. لذا، لا يوجد عدد من نتائج 7 قبل ظهور 12 بنسبة 50/50 تمامًا. إذا كنت تبحث عن رهان خاسر جيد، فننصحك إما بظهور أربع نتائج 7 قبل ظهور 12، أو ظهور 12 قبل ظهور خمس نتائج 7.

تم طرح هذا السؤال ومناقشته في منتدى موقعي المرافق Wizard of Vegas .

هل هناك طريقة سهلة لحساب احتمال الحصول على مجموع t باستخدام d نرد مكون من 6 أوجه؟

Anon E. Mouse

إليكم خدعة عملية، مقدمة من روبرت جودهاند من سومرست، المملكة المتحدة. أولًا، ضعوا ستة آحاد في صف واحد، محاطة بخمسة أصفار على كلا الجانبين، كما يلي:

احتمالات النرد الواحد

مجموع النرد 1 2 3 4 5 6
نرد واحد 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0

هذا يمثل عدد التركيبات الناتجة عن رمي نرد واحد من ١ إلى ٦. أعلم أن الأمر واضح جدًا. لكن تابع معي. لنردين، أضف صفًا آخر إلى الأسفل، ولكل خلية، احسب مجموع الصف الذي يسبقه والخمس خلايا على يساره. ثم أضف خمسة أصفار وهمية أخرى إلى اليمين، إذا أردت الاستمرار. هذا يمثل تركيبات رمي نرد إجمالي من ٢ إلى ١٢.

احتمالات النرد

مجموع النرد 2 3 4 5 6 7 8 9 10 11 12
نرد واحد 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0
نردتان 0 0 0 0 0 1 2 3 4 5 6 5 4 3 2 1 0 0 0 0 0

لثلاثة نرد، كرّر العملية. هذا يمثل عدد المجموعات من ٣ إلى ١٨.

توسيع احتمالات النرد الثلاثة

مجموع النرد 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
نرد واحد 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
نردتان 0 0 0 0 0 1 2 3 4 5 6 5 4 3 2 1 0 0 0 0 0 0 0 0 0 0
ثلاثة نرد 0 0 0 0 0 1 3 6 10 15 21 25 27 27 25 21 15 10 6 3 1 0 0 0 0 0

للحصول على احتمالية أي مجموع معطى، اقسم عدد مجموعات هذا المجموع على العدد الإجمالي للمجموعات. في حالة ثلاثة أحجار نرد، يكون المجموع 216، والذي يُحسب بسهولة أيضًا على أنه 6 3. على سبيل المثال، احتمالية الحصول على مجموع 13 بثلاثة أحجار نرد هي 21/216 = 9.72%.

بالنسبة لنرد d، ستحتاج إلى الانتقال من 1 إلى d-1. يمكن إنجاز ذلك بسهولة باستخدام أي جدول بيانات.

كم عدد رميات النرد التي يجب أن نحصل على فرصة 50/50 للحصول على الرقم 12 مرة واحدة على الأقل؟

Maff

هذه مسألة شائعة في تاريخ علم الاحتمالات. يعتقد الكثيرون خطأً أن الإجابة هي 18، لأن احتمال الحصول على 12 هو 1 من 36، و18×(1/36)=50%. ومع ذلك، ووفقًا لهذا المنطق، فإن احتمال الحصول على 12 في 36 رمية هو 100%، وهو أمر غير صحيح تمامًا. إليك الحل الصحيح. ليكن r هو عدد الرميات. احتمال ألا تكون الرمية 12 هو 35/36. احتمال وجود 0 رميات 12 في r رمية هو (35/36) r . لذا، علينا إيجاد r في المعادلة التالية:

(35/36) r = 0.5
log(35/36) r = log(0.5)
r × log(35/36) = log(0.5)
r = log(0.5)/log(35/36)
ر = 24.6051

إذن، لا توجد إجابة تقريبية. احتمال الحصول على ١٢ في ٢٤ رمية هو ١-(٣٥/٣٦) ٢٤ = ٤٩.١٤٪. واحتمال الحصول على ١٢ في ٢٥ رمية هو ١-(٣٥/٣٦) ٢٥ = ٥٠.٥٥٪.

إذا أردتَ المراهنة على هذا، فلنفترض أنك تستطيع الحصول على ١٢ في ٢٥ رمية، أو أن شخصًا آخر لا يستطيع ذلك في ٢٤ رمية. في كلتا الحالتين، ستكون لديك أفضلية عند تساوي المبلغ.

في لعبة حروب النرد ، ما احتمالية نجاح أي عدد مُحدد من النرد المهاجم والمدافع؟ كمهاجم، ما هي نسبة أعلى ربح متوقع؟

odiousgambit

لمن لا يعرف اللعبة، يقوم كلٌّ من المهاجم والمدافع برمي نرد من 1 إلى 8، وفقًا لعدد جيوش كلٍّ منهما في تلك المرحلة من المعركة. يفوز صاحب العدد الأكبر. أما المدافع فيتعادل. إذا خسر المهاجم، فسيحتفظ بجيش واحد في المنطقة التي بدأ منها الهجوم. لهذا السبب، يجب أن يكون لديه جيشان على الأقل للهجوم، فإذا فاز، يُمكن لأحدهما أن يسكن المنطقة المُحتلة والآخر أن يبقى.

يوضح الجدول التالي احتمال فوز المهاجم وفقًا لجميع التركيبات الـ 64 لإجمالي النرد.

احتمال فوز المهاجم

مهاجم المدافع
الجيش الأول جيشان 3 جيوش 4 جيوش 5 جيوش 6 جيوش 7 جيوش 8 جيوش
2 0.837963 0.443673 0.152006 0.035880 0.006105 0.000766 0.000071 0.000005
3 0.972994 0.778549 0.453575 0.191701 0.060713 0.014879 0.002890 0.000452
4 0.997299 0.939236 0.742831 0.459528 0.220442 0.083423 0.025450 0.006379
5 0.999850 0.987940 0.909347 0.718078 0.463654 0.242449 0.103626 0.036742
6 0.999996 0.998217 0.975300 0.883953 0.699616 0.466731 0.259984 0.121507
7 1.000000 0.999801 0.994663 0.961536 0.862377 0.685165 0.469139 0.274376
8 1.000000 0.999983 0.999069 0.989534 0.947731 0.843874 0.673456 0.471091

يوضح الجدول التالي الربح المتوقع للمهاجم، والمُعرَّف بـ pr (فوز المهاجم) * (عدد نرد المدافع) + pr (فوز المدافع) * (عدد نرد المهاجم -1). ويُظهر أن أكبر ربح متوقع هو الهجوم بـ 8 ضد خصم بـ 5.

صافي الربح من فوز المهاجم

مهاجم المدافع
الجيش الأول جيشان 3 جيوش 4 جيوش 5 جيوش 6 جيوش 7 جيوش 8 جيوش
2 0.675926 0.331019 -0.391976 -0.820600 -0.963370 -0.994638 -0.999432 -0.999955
3 0.918982 1.114196 0.267875 -0.849794 -1.575009 -1.880968 -1.973990 -1.995480
4 0.989196 1.696180 1.456986 0.216696 -1.236464 -2.249193 -2.745500 -2.929831
5 0.999250 1.927640 2.365429 1.744624 0.172886 -1.575510 -2.860114 -3.559096
6 0.999976 1.987519 2.802400 2.955577 1.996160 0.134041 -1.880192 -3.420409
7 1.000000 1.998408 2.951967 3.615360 3.486147 2.221980 0.098807 -2.158736
8 1.000000 1.999847 2.990690 3.884874 4.372772 3.970362 2.428384 0.066365

ما هو احتمال تكوين لعبة ياهتز باستخدام ما يصل إلى n لفة من النرد؟

مجهول

لفائدة القراء الآخرين، لعبة ياتزي هي لعبة خمسة من نفس النوع بخمسة نرد. في لعبة ياتزي، يمكن للاعب حمل أي نرد يشاء وإعادة رمي الباقي. يمكنه القيام بذلك حتى ثلاث رميات.

يمكن للاعب إعادة رمي النرد الذي كان يحمله سابقًا إن رغب. على سبيل المثال، إذا كانت رميته الأولى 3-3-4-5-6، وكان يحمل الرقم 3، ثم حصل على الرقم 3-3-5-5-5 بعد الرمية الثانية، فيمكنه الاحتفاظ بالرقم 5 وإعادة رمي الرقم 3 في رميته الثالثة.

يوضح الجدول التالي أقصى عدد من النرد المتشابه الوجه من رمية واحدة إلى 20. ويُظهر الجدول أن احتمالية الحصول على ياهتز خلال ثلاث رميات تبلغ حوالي 4.6%.

احتمالات ياتزي

لفات الحد الأقصى لعدد النرد من نفس الوجه
واحد اثنين ثلاثة أربعة خمسة
1 0.092593 0.694444 0.192901 0.019290 0.000772
2 0.008573 0.450103 0.409022 0.119670 0.012631
3 0.000794 0.256011 0.452402 0.244765 0.046029
4 0.000074 0.142780 0.409140 0.347432 0.100575
5 0.000007 0.079373 0.337020 0.413093 0.170507
6 0.000001 0.044101 0.263441 0.443373 0.249085
7 0.000000 0.024501 0.199279 0.445718 0.330502
8 0.000000 0.013612 0.147462 0.428488 0.410438
9 0.000000 0.007562 0.107446 0.398981 0.486011
10 0.000000 0.004201 0.077416 0.362855 0.555528
11 0.000000 0.002334 0.055317 0.324175 0.618174
12 0.000000 0.001297 0.039279 0.285674 0.673750
13 0.000000 0.000720 0.027757 0.249063 0.722460
14 0.000000 0.000400 0.019543 0.215313 0.764744
15 0.000000 0.000222 0.013720 0.184883 0.801175
16 0.000000 0.000124 0.009610 0.157896 0.832371
17 0.000000 0.000069 0.006719 0.134258 0.858954
18 0.000000 0.000038 0.004692 0.113753 0.881517
19 0.000000 0.000021 0.003272 0.096100 0.900607
20 0.000000 0.000012 0.002280 0.080994 0.916714


تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
أتساءل ما الذي سيأتي أكثر عند رمي زوج من النرد - مجموع فردي أم زوجي؟

relaxmax

الإجابة هي ٥٠/٥٠. ينطبق هذا على أي عدد من النرد، وليس فقط على اثنين.

قد يكون هذا بعيدًا عن الموضوع، لكنني لطالما اعتقدتُ أن مجموعة رهانات فردية/زوجية ستكون طريقة جيدة لاستبدال رهانات 6/8 الكبيرة المزعجة في لعبة الكرابس. ولمنح الكازينو أفضلية، إليكم جداول الدفع المقترحة وتحليلاتي.

رهان فردي

حدث يدفع التركيبات احتمال يعود
3 أو 11 1.5 4 0.111111 0.166667
5 أو 9 1 8 0.222222 0.222222
7 0.5 6 0.166667 0.083333
حتى -1 18 0.500000 -0.500000
المجموع 36 1.000000 -0.027778

حتى الرهان

حدث يدفع التركيبات احتمال يعود
2 أو 12 3 2 0.055556 0.166667
4 أو 10 1 6 0.166667 0.166667
6 أو 8 0.5 10 0.277778 0.138889
غريب -1 18 0.500000 -0.500000
المجموع 36 1.000000 -0.027778


يرجى ملاحظة أنني أطالب بجميع الحقوق المتعلقة بهذا المنشور.

تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
في مكافأة Hot Roll، يفوز اللاعب بعدد العملات المعدنية التالي وفقًا لمجموع نردين:

  • 2 أو 12: 1000
  • 3 أو 11: 600
  • 4 أو 10: 400
  • 5 أو 9: 300
  • 6 أو 8: 200


يستمر في رمي النرد حتى يحصل على سبعة، فتنتهي المكافأة. إذا حصل على سبعة في الرمية الأولى، يحصل على جائزة ترضية قدرها 700 عملة. ما متوسط العملات التي يربحها كل مكافأة؟

مجهول

متوسط عدد الرميات هو معكوس حدث نهاية المكافأة، والذي احتماله ١/٦، لذا سيرمي اللاعب ست مرات في المتوسط. مع ذلك، ستكون الرمية الأخيرة هي السابعة، أي بمتوسط خمس رميات فائزة لكل مكافأة.

فيما يلي احتمال كل إجمالي، بافتراض عدم وجود سبعة:

  • 2 أو 12: 1/30
  • 3 أو 11: 2/30
  • 4 أو 10: 3/30
  • 5 أو 9: 4/30
  • 6 أو 8: 5/30


لذا، فإن متوسط الفوز لكل لفة، بافتراض عدم وجود سبعة، هو 2*[(1/30)*1000 + (2/30)*600 + (3/30)*400 + (4/30)*300 + (5/30)*200] = 373.33.

قيمة جائزة الترضية هي (1/6)*700 = 116.67.

وبالتالي، فإن متوسط الفوز بالمكافأة هو 116.67 + 5×373.33 = 1983.33.

ما هو الحل لمشكلة النرد في عمود "اسأل المعالج" رقم 179 ، إذا تناوب اللاعبون على رمي النرد وكان اللاعب الذي يقوم بالرمي هو الوحيد الذي يمكنه التقدم بناءً على الرمية؟

مجهول

هذا هو السؤال الأصلي المنشور في العمود رقم 179: إذا تم رمي حجرين من النرد مرارًا وتكرارًا، حتى يحدث أي من الحدثين التاليين، فما هو الأكثر احتمالًا أن يحدث أولاً:

  • يتم الحصول على مجموع ستة وثمانية، بأي ترتيب، مع السماح بالتكرارات.
  • يتم الحصول على العدد سبعة مرتين.

المفاجأة هي أن نفس الرمية لا تفيد كلا اللاعبين. بدلًا من ذلك، يتناوبان على الرمي، وفقط من يرمي يمكنه استخدامها.

تعتمد الإجابة على من يبدأ الرمي. إذا بدأ اللاعب الذي يحتاج إلى رقمي ستة وثمانية أولاً، فإن احتمال فوزه هو ٥٧٫٤٨٧٢٩٤٪. أما إذا بدأ اللاعب الذي يحتاج إلى رقمي سبعة أولاً، فإن احتمال فوزه هو ٥٢٫٦٧١٦١٤٪. لقد حللتُ المسألة باستخدام عملية سلسلة ماركوف البسيطة.

تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .

لنفترض أن لديك ١٢ حجر نرد سداسي الأوجه. ترميها، ويمكنك ترك أي حجر نرد تريده. ثم تعيد رمي الحجر الآخر. ما احتمال الحصول على ١٢ حجر نرد متماثل في الرميتين؟

مجهول

هناك 58 نوعًا مختلفًا من التسلسلات في الرمية الأولى. أُحدد كل نوع برقم وجه الأغلبية، ثم عدد أحجار النرد التي تحمل الوجه الثاني إجمالًا، وهكذا. على سبيل المثال، رمية الأرقام 3، 3، 3، 6، 6، 6، 5، 5، 2 تُمثل 4-3-2-1. يوضح الجدول التالي عدد تركيبات كل تسلسل، واحتمالية ظهوره، واحتمالية الحصول على 12 عددًا متماثلًا في الرمية الثانية، وحاصل ضرب العددين. بالنسبة لاحتمالية الرمية الثانية، أفترض أن اللاعب يحمل النرد الذي حصل على أكبر مجموع في الرمية الأولى. تُظهر الخلية السفلية اليمنى احتمالًا كليًا قدره 0.0000037953، أي ما يعادل 1 من 263,486.

سؤال النرد 12

تسلسل التركيبات احتمال
تسلسل		 شرطي
احتمال		 المجموع
احتمال
12-0-0-0-0-0 6 0.0000000028 1.0000000000 0.0000000028
11-1-0-0-0-0 360 0.0000001654 0.1666666667 0.0000000276
10-2-0-0-0-0 1,980 0.0000009096 0.0277777778 0.0000000253
10-1-1-0-0-0 7,920 0.0000036384 0.0277777778 0.0000001011
9-3-0-0-0-0 6,600 0.0000030320 0.0046296296 0.0000000140
9-2-1-0-0-0 79,200 0.0000363840 0.0046296296 0.0000001684
9-1-1-1-0-0 79,200 0.0000363840 0.0046296296 0.0000001684
8-4-0-0-0-0 14,850 0.0000068220 0.0007716049 0.0000000053
8-3-1-0-0-0 237,600 0.0001091519 0.0007716049 0.0000000842
8-2-2-0-0-0 178,200 0.0000818639 0.0007716049 0.0000000632
8-2-1-1-0-0 1,069,200 0.0004911837 0.0007716049 0.0000003790
8-1-1-1-1-0 356,400 0.0001637279 0.0007716049 0.0000001263
7-5-0-0-0-0 23,760 0.0000109152 0.0001286008 0.0000000014
7-4-1-0-0-0 475,200 0.0002183039 0.0001286008 0.0000000281
7-3-2-0-0-0 950,400 0.0004366077 0.0001286008 0.0000000561
7-3-1-1-0-0 2,851,200 0.0013098232 0.0001286008 0.0000001684
7-2-2-1-0-0 4,276,800 0.0019647348 0.0001286008 0.0000002527
7-2-1-1-1-0 5,702,400 0.0026196464 0.0001286008 0.0000003369
7-1-1-1-1-1 570,240 0.0002619646 0.0001286008 0.0000000337
6-6-0-0-0-0 13,860 0.0000063672 0.0000214335 0.0000000001
6-5-1-0-0-0 665,280 0.0003056254 0.0000214335 0.0000000066
6-4-2-0-0-0 1,663,200 0.0007640635 0.0000214335 0.0000000164
6-4-1-1-0-0 4,989,600 0.0022921906 0.0000214335 0.0000000491
6-3-3-0-0-0 1,108,800 0.0005093757 0.0000214335 0.0000000109
6-3-2-1-0-0 19,958,400 0.0091687624 0.0000214335 0.0000001965
6-3-1-1-1-0 13,305,600 0.0061125083 0.0000214335 0.0000001310
6-2-2-2-0-0 4,989,600 0.0022921906 0.0000214335 0.0000000491
6-2-2-1-1-0 29,937,600 0.0137531436 0.0000214335 0.0000002948
6-2-1-1-1-1 9,979,200 0.0045843812 0.0000214335 0.0000000983
5-5-2-0-0-0 997,920 0.0004584381 0.0000035722 0.0000000016
5-5-1-1-0-0 2,993,760 0.0013753144 0.0000035722 0.0000000049
5-4-3-0-0-0 3,326,400 0.0015281271 0.0000035722 0.0000000055
5-4-2-1-0-0 29,937,600 0.0137531436 0.0000035722 0.0000000491
5-4-1-1-1-0 19,958,400 0.0091687624 0.0000035722 0.0000000328
5-3-3-1-0-0 19,958,400 0.0091687624 0.0000035722 0.0000000328
5-3-2-2-0-0 29,937,600 0.0137531436 0.0000035722 0.0000000491
5-3-2-1-1-0 119,750,400 0.0550125743 0.0000035722 0.0000001965
5-3-1-1-1-1 19,958,400 0.0091687624 0.0000035722 0.0000000328
5-2-2-2-1- 59,875,200 0.0275062872 0.0000035722 0.0000000983
5-2-2-1-1-1 59,875,200 0.0275062872 0.0000035722 0.0000000983
4-4-4-0-0-0 693,000 0.0003183598 0.0000005954 0.0000000002
4-4-3-1-0-0 24,948,000 0.0114609530 0.0000005954 0.0000000068
4-4-2-2-0-0 18,711,000 0.0085957147 0.0000005954 0.0000000051
4-4-2-1-1-0 74,844,000 0.0343828589 0.0000005954 0.0000000205
4-4-1-1-1-1 12,474,000 0.0057304765 0.0000005954 0.0000000034
4-3-3-2-0-0 49,896,000 0.0229219060 0.0000005954 0.0000000136
4-3-3-1-1-0 99,792,000 0.0458438119 0.0000005954 0.0000000273
4-3-2-2-1-0 299,376,000 0.1375314358 0.0000005954 0.0000000819
4-3-2-1-1-1 199,584,000 0.0916876238 0.0000005954 0.0000000546
4-2-2-2-2-0 37,422,000 0.0171914295 0.0000005954 0.0000000102
4-2-2-2-1-1 149,688,000 0.0687657179 0.0000005954 0.0000000409
3-3-3-3-0-0 5,544,000 0.0025468784 0.0000000992 0.0000000003
3-3-3-2-1-0 133,056,000 0.0611250826 0.0000000992 0.0000000061
3-3-3-1-1-1 44,352,000 0.0203750275 0.0000000992 0.0000000020
3-3-2-2-2-0 99,792,000 0.0458438119 0.0000000992 0.0000000045
3-3-2-2-1-1 299,376,000 0.1375314358 0.0000000992 0.0000000136
3-2-2-2-2-1 149,688,000 0.0687657179 0.0000000992 0.0000000068
2-2-2-2-2-2 7,484,400 0.0034382859 0.0000000165 0.0000000001
المجموع 2,176,782,336 1.0000000000 0.0000037953
في المتوسط، كم عدد لفات النرد العادل اللازمة لتدوير كل وجه مرتين على الأقل؟

Ace2

انقر على الزر أدناه للحصول على الإجابة.

الإجابة هي 1,172,906,043 / 48,600,000 = تقريبًا 24.13387

هذا هو الحل الخاص بي. (PDF)

تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .

لنفترض أن حجر نرد سداسي الأوجه رُمي حتى ظهر الرقم ١، ٢، ٣، أو ٦. إذا كان أول رقم يظهر في نهاية اللعبة هو ١، ٢، أو ٣، فلن تربح شيئًا. أما إذا كان أول رقم يظهر في نهاية اللعبة هو ٦، فستربح دولارًا واحدًا لكل رمية نرد. ما متوسط ربح هذه اللعبة؟

Klopp

انقر على الزر أدناه للحصول على بعض صيغ السلسلة اللانهائية التي قد تجدها مفيدة.

[المفسد=تلميحات]

تلميح 1: مجموع i = 0 إلى ∞ من n i = 1 / (1-n)

تلميح 2: مجموع i = 0 إلى ∞ من i × n i = n / (1-n) 2

[/spoiler]

انقر على الزر أدناه للحصول على الإجابة.

الإجابة هي 3/4.

انقر على الزر أدناه للحصول على الحل.

لنفترض أن حجر نرد سداسي الأوجه رُمي حتى ظهر الرقم ١، ٢، ٣، أو ٦. إذا كان أول رقم يظهر في نهاية اللعبة هو ١، ٢، أو ٣، فلن تربح شيئًا. أما إذا كان أول رقم يظهر في نهاية اللعبة هو ٦، فستربح دولارًا واحدًا لكل رمية نرد. ما متوسط ربح هذه اللعبة؟

تلميح 1: مجموع i = 0 إلى ∞ من n i = 1 / (1-n)

تلميح 2: مجموع i = 0 إلى ∞ من i × n i = n / (1-n) 2

يمكن التعبير عن الفوز المتوقع كمجموع i = 0 إلى ∞ من (1 + i) * (1/3) i * (1/6). =

(1/6) * مجموع i = 0 إلى ∞ من (1/3) i + (1/6) * مجموع i = 0 إلى ∞ من (i * (1/3) i ).

دعونا نقوم بتقييم هذه الأمور واحدة تلو الأخرى.

المجموع لـ i = 0 إلى ∞ من (1/3) i =

1 / (1 - (1/3)) =

1 / (2/3) =

3/2

المجموع لـ i = 0 إلى ∞ من (i * (1/3) i ) =

(1/3) / (1 - (1/3)) 2 =

(1/3) / (4/9) =

(1/3) * (9/4) =

3/4

إذا جمعنا كل ذلك معًا، فإن الإجابة هي

(1/6) * (3/2) + (1/6) * (3/4) =

(1/4) + (1/8) =

3/8

تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .

ما هو العدد المتوقع من رميات النرد العادل لتدوير كل وجه مرتين على الأقل؟

Ace2

الإجابة هي 390968681 / 16200000 = تقريبًا 24.13386919753086

مع أنه يمكن حل هذه المشكلة باستخدام سلسلة ماركوف طويلة ومملة، إلا أنني أُفضّل الحل الشامل. أشرح كيفية استخدام هذه الطريقة في صفحاتي حول رهان النار ومكافآت الكرابس .

تخيل أنه بدلاً من تحديد الأحداث المهمة برمي النرد، واحدة تلو الأخرى، اعتبرها لحظة زمنية. افترض أن الوقت الفاصل بين الأحداث لا يعتمد على الذاكرة، حيث يبلغ متوسطه وحدة زمنية واحدة. بمعنى آخر، يتبع الوقت الفاصل بين الأحداث توزيعًا أُسيًا بمتوسط 1. لن يكون هذا مهمًا عند تقييم الرهان، لأن الأحداث لا تزال تقع واحدة تلو الأخرى.

وفقًا لتوزيع بواسون، فإن احتمالية رمي أي جانب من جوانب النرد صفر مرة في x وحدات زمنية هي exp(-x/6)*(x/6) 0/0 ! = exp(-x/6). ويقول بواسون أيضًا إن احتمالية رمي أي جانب مرة واحدة بالضبط هي exp(-x/6)*(x/6) 1/1 ! = exp(-x/6) * (x/6). وبالتالي فإن احتمالية رمي أي جانب مرتين أو أكثر في x وحدات زمنية هي 1 - exp(-x/6)*(1 + (x/6)). واحتمالية رمي جميع الجوانب الستة مرتين على الأقل هي (1 - exp(-x/6)*(1 + (x/6))) 6. واحتمالية عدم رمي جانب واحد على الأقل مرتين على الأقل تساوي:

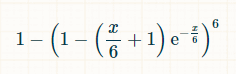
لف كل جانب مرتين

نحن بحاجة إلى دمج ذلك على مدار الوقت لمعرفة مقدار الوقت الذي سيمضي، في المتوسط، حيث لم يتم تحقيق الهدف المطلوب.

لحسن الحظ، يُمكننا استخدام حاسبة تكامل في هذه المرحلة. بالنسبة للحاسبة المُرفقة، ضع 1- (1 - exp(-x/6)*(1 + x/6))^6 dx = apx. 24.1338692 في مربع النص التالي لـ "حساب تكامل"، وتحت "مخصص"، اضبط حد التكامل من 0 إلى ∞.

الإجابة هي 390968681 / 16200000 = تقريبًا 24.13386919753086

تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .

ابدأ بنرد ذي ستة أوجه عادلة، ثم رميته ست مرات، وسجل نتائج كل رمية. ثم اكتب هذه الأرقام على الوجوه الستة لنرد عادل آخر غير مُسمّى. على سبيل المثال، إذا كانت رمياتك الست هي 3، 5، 3، 6، 1، و2، فلن يكون على النرد الثاني الرقم 4؛ بل سيكون عليه رقمان 3.

بعد ذلك، تُلقي حجر النرد الثاني ست مرات. تأخذ هذه الأرقام الستة وتكتبها على وجوه حجر نرد عادل آخر، ثم تُكمل عملية توليد حجر نرد جديد من الحجر السابق.

في النهاية، ستحصل على نرد بنفس الرقم على جميع أوجهه الستة. ما هو متوسط عدد مرات الانتقال من نرد لآخر (أو إجمالي الرميات مقسومًا على 6) للوصول إلى هذه الحالة؟

rsactuary

تقريبًا 9.65599148388557

لتجنب الالتباس، دعونا نُسمّي النرد الأولي بالأحرف بدلًا من الأرقام. دعونا نُسمّي كل حالة ممكنة للنرد بالأحرف. على سبيل المثال، AAABBC تعني ثلاثة من حرف واحد، واثنين من حرف آخر، وواحد من ثالث. الحالة الأولية ستكون ABCDEF.

ليكن E(ABCDEF) هو العدد المتوقع للرميات من الحالة ABCDEF.

E(ABCDEF) = 1 + [180 × E(AAAAAB) + 450 × E(AAAABB) + 300 × E(AAABBB) + 1800 × E(AAAABC) + 7200 × E(AAABBC) + 1800 × E(AABBCC) + 7200 × E(AAABCD) + 16200 × E(AABBCD) + 10800 × E(AABCDE) + 720 × E(ABCDEF)]/46656

بناءً على عدد تركيبات الانتقال من حالة إلى أخرى، تُظهر مصفوفة الانتقال التالية عدد الطرق للانتقال من كل حالة ابتدائية (العمود الأيسر) إلى كل حالة جديدة. استغرق بناء هذه المصفوفة بشكل صحيح بضع ساعات.

مصفوفة الانتقال أ

ولاية
قبل		 أأأأ أأأأب أأأأب أأأأأأ أأأبب AAABBC AABBCC أأأب ج د أأ ب ب ج د AABCDE أ ب ج د هـ
أأأأب 15,626 18,780 9,750 2500 - - - - - - -
أأأأب 4,160 13,056 19,200 10,240 - - - - - - -
أأأأأأ 1,458 8,748 21,870 14,580 - - - - - - -
أأأب سي 4,098 12,348 8,190 2,580 7,920 10,080 1,440 - - - -
AAABBC 794 5,172 8,670 5,020 6,480 17,280 3,240 - - - -
AABBCC 192 2,304 5,760 3,840 5,760 23,040 5,760 - - - -
أأأب ج د 732 4,464 4,140 1,680 7,920 14,400 2,520 4,320 6,480 - -
أأ ب ب ج د 130 1,596 3,150 1,940 5,280 16,800 3,600 4,800 9,360 - -
AABCDE 68 888 1,380 760 3,960 11,520 2,520 7,200 14,040 4,320 -
أ ب ج د هـ 6 180 450 300 1800 7,200 1800 7,200 16,200 10,800 720

لن أدخل في محاضرة طويلة عن جبر المصفوفات، باستثناء أن نقول أن المصفوفة B هي كما يلي:

المصفوفة ب

ولاية
قبل		 أأأأب أأأأب أأأأأأ أأأب سي AAABBC AABBCC أأأب ج د أأ ب ب ج د AABCDE أ ب ج د هـ
أأأأب -27876 9750 2500 0 0 0 0 0 0 -46656
أأأأب 13056 -27456 10240 0 0 0 0 0 0 -46656
أأأأأأ 8748 21870 -32076 0 0 0 0 0 0 -46656
أأأب سي 12348 8190 2580 -38736 10080 1440 0 0 0 -46656
AAABBC 5172 8670 5020 6480 -29376 3240 0 0 0 -46656
AABBCC 2304 5760 3840 5760 23040 -40896 0 0 0 -46656
أأأب ج د 4464 4140 1680 7920 14400 2520 -42336 6480 0 -46656
أأ ب ب ج د 1596 3150 1940 5280 16800 3600 4800 -37296 0 -46656
AABCDE 888 1380 760 3960 11520 2520 7200 14040 -42336 -46656
أ ب ج د هـ 180 450 300 1800 7200 1800 7200 16200 10800 -46656

الجواب هو محدد المصفوفة B لمحدد المصفوفة A:

تحديد (أ) = 1,461,067,501,120,670,000,000,000,000,000,000,000,000,000,000

تحديد (ب) = 14,108,055,348,203,100,000,000,000,000,000,000,000,000,000,000,000

تحديد (ب) / تحديد (أ) = تقريبًا 9.65599148388557

إذا قمت برمي حجر نرد واحد 20 مرة، ما هو احتمال أن تضرب جميع الجوانب الستة مرة واحدة على الأقل؟

Ace2

الإجابة هي تقريبًا 0.847987541

يمكن تقريب الإجابة على النحو التالي: 1 - (احتمال (لا يوجد 1) + احتمال (لا يوجد 2) + ... + احتمال (لا يوجد 6)) = 1 - 6*(5/6)^20 = تقريبًا 0.84349568.

مع ذلك، سيؤدي ذلك إلى طرح مضاعف للحالات التي لم يُرمى فيها وجهان مختلفان. هناك combin(6,2)=15 طريقة لاختيار وجهين من أصل ستة. احتمال عدم رمي أي وجهين معلومين هو (4/6)^20. علينا إضافة هذه الاحتمالات إلى الاحتمال، لأنها طُرحت مرتين في الخطوة السابقة. إذن، لدينا الآن 1 - 6*(5/6)^20 + 15*(4/6)^20 = تقريبًا 0.84800661.

تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .

مع ذلك، إذا طُرِحَت أي مجموعة من ثلاثة أضلاع لم تُدحرج قط، لتُضاف ثلاثة أضلاع في الخطوة الأولى وتُطرح ثلاثة أضلاع في الخطوة الثانية. علينا طرحها مجددًا في حالة عدم دحرجة جميع الأضلاع الستة. هناك 20 طريقة لاختيار ثلاثة أضلاع من أصل ستة. احتمال عدم دحرجة أي ثلاثة أضلاع محددة هو (3/6)^20. إذن، لدينا الآن 1 - 6*(5/6)^20 + 15*(4/6)^20 - 20*(3/6)^20 = تقريبًا 0.847987537.

مع ذلك، إذا طُرِحَت أي مجموعة من أربعة أضلاع لم تُدحرج قط، أربع مرات في الخطوة الأولى، ثم جُمِعَت أربع مرات في الخطوة الثانية، ثم طُرِحَت أربع مرات في الخطوة الثالثة. علينا إعادة جمعها، لأن كل حالة من هذه الحالات طُرِحَت مرتين بالفعل. هناك 15 طريقة لاختيار أربعة أضلاع من أصل ستة. احتمال عدم دحرجة أي أربعة أضلاع محددة هو (2/6)^20. إذن، لدينا الآن 1 - 6*(5/6)^20 + 15*(4/6)^20 - 20*(3/6)^20 + 15*(2/6)^20 = تقريبًا 0.84798754089.

مع ذلك، لو كانت جميع الرميات العشرين متطابقة، لكان هذا الوضع قد طُرح خمس مرات في الخطوة الأولى، ثم جُمعت خمس مرات في الخطوة الأولى، ثم طُرح خمس مرات في الخطوة الثالثة، ثم جُمعت خمس مرات في الخطوة الرابعة. علينا طرحها مجددًا. إذن، لدينا الآن 1 - 6*(5/6)^20 + 15*(4/6)^20 - 20*(3/6)^20 + 15*(2/6)^20 - 6*(1/6)^20 = تقريبًا 0.84798754089.

إذن الإجابة هي 1-6*(5/6)^20+COMBIN(6,4)*(4/6)^20-COMBIN(6,3)*(3/6)^20+COMBIN(6,2)*(2/6)^20-6*(1/6)^20 = تقريبًا 0.84798754089.

لديك مكعبان. يمكنك ترقيم كل جانب من النردين كما تشاء، طالما أن كل جانب عدد صحيح أكبر من أو يساوي واحدًا. يمكنك تكرار الرقم نفسه على نفس النرد، والارتقاء إلى أي عدد تريده. بخلاف إنشاء نرد قياسي، كيف يمكنك ترقيمهما بحيث يكون احتمال أي مجموع معطى مساويًا لاحتمال النرد القياسي؟

مجهول

النرد 1 = 1،2،2،3،3،4.
النرد 2 = 1،3،4،5،6،8.

أخشى أن حلي لهذه المشكلة كان عبارة عن تجربة وخطأ إلى حد كبير.

ما هو متوسط عدد اللفات اللازمة باستخدام نردين لتحقيق مجموع من 2 إلى 12؟

مجهول

الإجابة هي 769767316159 / 12574325400 = تقريبًا 61.2173847639572.

يمكن استخدام سلسلة ماركوف للإجابة على هذا السؤال، لكنني أُفضّل التفاضل والتكامل. يكمن السر في أن تكون الإجابة واحدة إذا كان الزمن بين الرميات موزعًا أسيًا بمتوسط يساوي واحدًا. مع ذلك، يمكن التعبير عن الإجابة بالتكامل من صفر إلى ما لا نهاية لما يلي:

1-(1-exp(-x/36))^2*(1-exp(-x/18))^2*(1-exp(-x/12))^2*(1-exp(-x/9))^2*(1-exp(-5*x/36))^2*(1-exp(-x/6))

يمكنك حل مثل هذه التكاملات بسهولة باستخدام حاسبة التكامل .

يمكنك أيضًا حل أي مشكلة من هذا القبيل باستخدام حاسبة التجارب المتوقعة الخاصة بي.

لعبة "دروب ديد" تُلعب بخمسة أحجار نرد قياسية. تبدأ دورك برمي جميع الأحجار الخمسة. إذا لم يكن أي منها 2 أو 5، تجمع مجموع الأحجار، وتضيفه إلى مجموع نقاطك، ثم ترميه مرة أخرى. إذا رميت أي أحجار نرد تحمل الرقم 2 أو 5، تكون نتيجتك صفرًا. تُعلن جميع الأحجار التي تحمل الرقم 2 أو 5 ميتة وتُستبعد. ثم ترميها مرة أخرى بالنرد المتبقي. يستمر اللعب إما بتسجيل نقاط أو إزالة الأحجار. ينتهي دورك بإخراج جميع الأحجار، وعندها يُقال إنك ميت. تُجمع جميع رمياتك للحصول على نتيجتك النهائية. أعلى نتيجة تفوز.

ما هي نتيجتك المتوقعة لهذه المباراة؟

Gialmere

16.064662

لنبدأ بالسيناريو الذي يتبقى فيه نرد واحد ونتحرك للخلف.

دع المتغير a يكون النقاط الإضافية المتوقعة مع بقاء نرد واحد.

المتوسط الذي لا يساوي 2 أو 5 هو (1+3+4+6)/4 = 7/2.

أ = (2/3)×(أ + 7/2).

أ/3 = 7/3.

أ = 7.

الآن، دعنا نحسب b، النقاط المتوقعة مع وجود نردين متبقيين.

ب = (2/3) 2 ×(ب + 2 × (7/2)) + 2×(2/3)×(1/3)×أ.

ب = 11.2.

الآن، دعنا نحسب c، النقاط المتوقعة مع وجود ثلاثة أحجار نرد متبقية.

ج = (2/3) 3 ×(ج + 3× (7/2)) + 3×(2/3) 2 ×(1/3)×ب + 3×(2/3)×(1/3) 2 ×ب.

ج = 1302/95 = 13.705263.

الآن، دعنا نحسب d، النقاط المتوقعة مع وجود أربعة أحجار نرد متبقية.

د = (2/3) 4 ×(د + 4× (7/2)) + 4×(2/3) 3 ×(1/3)×ج + 6×(2/3) 2 ×(1/3) 2 ×ب + 4×(2/3)×(1/3) 3 ×أ.

د = 3752/247 = 15.190283.

أخيرًا، دعنا نحسب e، النقاط المتوقعة مع وجود خمسة نرد متبقية.

ه = (2/3) 5 ×(e + 5×(7/2)) + 5×(2/3) 4 ×(1/3)×d + 10×(2/3) 3 ×(1/3) 2 ×c + 10×(2/3) 2 ×(1/3) 3 ×b + 5×(2/3)×(1/3) 4 ×أ.

هـ = 16.064662.

تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .

ألقِ حجري نرد، أحمر وأزرق، مرارًا وتكرارًا. سجّل مجموع رميات كل حجر نرد. ما هو العدد المتوقع للأدوار حتى يتساوى المجموعان؟

teliot

الجواب هو اللانهاية.

من الصعب تفسير كون الإجابة هي اللانهاية. ومما يزيد الأمر تعقيدًا وتناقضًا، أن احتمال تساوي المجموعين هو 1.

يوضح الجدول التالي احتمالية أن تكون الإجماليات هي نفسها للمرة الأولى بعد 1 إلى 16 لفة.

احتمالات تساوي المجموع في المرة الأولى

لفات احتمال
1 0.166667
2 0.112654
3 0.092850
4 0.080944
5 0.072693
6 0.066539
7 0.061722
8 0.057819
9 0.054573
10 0.051819
11 0.049443
12 0.047367
13 0.045532
14 0.043895
15 0.042423
16 0.041089

يُظهر برنامج Excel ملاءمة قريبة جدًا لهذا المنحنى وهي y = 0.1784*x-1.011، حيث x = عدد اللفات وy = الاحتمال.

مجموع هذه السلسلة اللانهائية هو اللانهاية.

تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .

تم رمي خمسة نرد حمراء وخمسة نرد زرقاء. ما احتمال أن تكون النتيجة نفسها لكلا النردين، بغض النظر عن الترتيب؟ على سبيل المثال، النتيجة في كلتا الرميتين هي ١-٢-٣-٣-٦؟

مجهول

3,557 / 559,872 = 0.006353238، أو حوالي 1 / 157.

يوضح الجدول التالي أي نوع من اللفائف:

  • عدد الطرق المختلفة لتحقيق هذه النتيجة. على سبيل المثال، للحصول على فول هاوس، هناك ست مجموعات للثلاثة من نفس النوع، وخمس مجموعات للزوج، بإجمالي 30 فول هاوس مختلفة.
  • عدد الطلبات. على سبيل المثال، للحصول على منزل كامل، هناك 10 طرق لاختيار ثلاثة من خمسة أحجار نرد للحصول على ثلاثة من نفس النوع. يجب أن يكون لدى الحجرين الآخرين زوج من الأحجار.
  • عدد طرق رمي النرد. هذا هو حاصل ضرب العمودين الأولين. على سبيل المثال، هناك 30 × 10 = 300 طريقة لرمي النرد (فول هاوس).
  • احتمالية الفوز. على سبيل المثال، في حالة "فول هاوس"، الاحتمال هو ٣٠٠/٦ = ٠ ٫٠٣٨٥٨٠.
  • احتمال أن تكون كلتا الرميتين متماثلتين، وأن تكونا من اليد المعطاة. هذا هو الاحتمال من العمود الرابع مُربعًا مقسومًا على العمود الثاني. على سبيل المثال، احتمال أن تكون كلتا الرميتين فول هاوس هو 0.038580 2. ومع ذلك، فإن احتمال أن تكون كلتا الرميتين نفس البيت هو 1/30. لذا، فإن احتمال أن تكون كلتا الرميتين نفس الفول هاوس هو 0.038580 2/30 = 0.00004961.

تُظهر الخلية اليمنى السفلية إجمالي احتمالية أن تكون كلتا اللفافتين متماثلتين وهي 0.00635324.

لفة مطابقة

يكتب
من لفة		 مختلف
أنواع		 طلبات المجموع
التركيبات		 احتمال
لفة واحدة		 احتمال
لفافتين
خمسة من نوع واحد 6 1 6 0.00077160 0.00000010
أربعة من نفس النوع 30 5 150 0.01929012 0.00001240
منزل كامل 30 10 300 0.03858025 0.00004961
ثلاثة من نفس النوع 60 20 1200 0.15432099 0.00039692
زوجان 60 30 1800 0.23148148 0.00089306
زوج 60 60 3,600 0.46296296 0.00357225
خمسة مفردة 6 120 720 0.09259259 0.00142890
المجموع 7,776 1.00000000 0.00635324

يتم رمي نرد سداسي الأوجه حتى يحدث أحد الحدثين التاليين:

أ) ظهر أي جانب ست مرات.
ب) كل جانب ظهر مرة واحدة على الأقل.

ما هو احتمال وقوع الحدث A أولاً؟

Ace2

للإجابة على هذا السؤال كما فعلت، باستخدام حساب التفاضل والتكامل، أوصي باستخدام آلة حاسبة للتكامل مثل تلك الموجودة على integral-calculator.com/ .

تقريبًا 0.252635881662548

وهنا الحل الخاص بي (PDF).

تم طرح هذه المشكلة (بكلمات مختلفة قليلاً) ومناقشتها في منتدياتي في Wizard of Vegas .

ترغب في لعب لعبة تتطلب نردًا عاديًا سداسي الأوجه. للأسف، فقدت النرد. مع ذلك، لديك أربع بطاقات فهرسة، يمكنك وضع علامات عليها بالطريقة التي تريدها. على اللاعب اختيار بطاقتين عشوائيًا من الأربع، دون استبدال، وحساب مجموع البطاقتين.

كيف يمكنك ترقيم البطاقات بحيث يمثل مجموع بطاقتين مختلفتين رمية النرد؟

Gialmere

رقمهم 0، 1، 2، و 4.

هناك ست طرق لسحب بطاقتين من أصل أربع بطاقات، على النحو التالي.

  • 0+1 = 1
  • 0+2 = 2
  • 1+2 = 3
  • 0+4 = 4
  • 1+4 = 5
  • 2+4 = 6

تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .

يُرمى حجر نرد سداسي الأوجه مرارًا وتكرارًا حتى يصبح مجموع الرميات ١٣ أو أكثر. ما هو المتوسط الحسابي والوسيط والمنوال للمجموع النهائي؟

Gialmere

المتوسط = 14.690219
المتوسط = 14
الوضع = 13

اضطررتُ لاستخدام سلسلة ماركوف في هذه الحالة. يوضح الجدول التالي احتمال كل مجموع نهائي وفقًا للمجموع المتسلسل في العمود الأيسر. ابدأ بالحالات الواضحة للمجموعات من ١٣ إلى ١٨. ثم، للمجموعات المتسلسل من ٠ إلى ١٢، احسب متوسط الخلايا الست أدناه.

يمكن العثور على احتمالات الحالة الأولية في الصف الأول لمجموع 0.

سلسلة ماركوف

مجموع اللفات 13 14 15 16 17 18
0 0.279263 0.236996 0.192313 0.145585 0.097371 0.048472
1 0.290830 0.230791 0.188524 0.143842 0.097114 0.048899
2 0.293393 0.241931 0.181893 0.139625 0.094943 0.048215
3 0.289288 0.245178 0.193717 0.133678 0.091410 0.046728
4 0.280369 0.242560 0.198450 0.146988 0.086950 0.044682
5 0.268094 0.235687 0.197878 0.153768 0.102306 0.042267
6 0.253604 0.225827 0.193419 0.155611 0.111500 0.060039
7 0.360232 0.193566 0.165788 0.133380 0.095572 0.051462
8 0.308771 0.308771 0.142104 0.114326 0.081919 0.044110
9 0.264660 0.264660 0.264660 0.097994 0.070216 0.037809
10 0.226852 0.226852 0.226852 0.226852 0.060185 0.032407
11 0.194444 0.194444 0.194444 0.194444 0.194444 0.027778
12 0.166667 0.166667 0.166667 0.166667 0.166667 0.166667
13 1.000000 0.000000 0.000000 0.000000 0.000000 0.000000
14 0.000000 1.000000 0.000000 0.000000 0.000000 0.000000
15 0.000000 0.000000 1.000000 0.000000 0.000000 0.000000
16 0.000000 0.000000 0.000000 1.000000 0.000000 0.000000
17 0.000000 0.000000 0.000000 0.000000 1.000000 0.000000
18 0.000000 0.000000 0.000000 0.000000 0.000000 1.000000

تم طرح هذا السؤال ومناقشته في منتدى Wizard of Vegas .

كما تعلمون، فإن الرهان الشامل في لعبة الكرابس يفوز إذا تم رمي كل مجموع من 2 إلى 12، باستثناء 7، قبل 7. كم عدد اللفات في المتوسط التي يجب أن تفوز بها بهذا الرهان، عندما تفوز؟

Ace2

20.989727251191...

وهنا الحل الخاص بي (PDF).

تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .

أرى أحدهم يدّعي أنه شاهد ١٨ رمية متتالية (ما مجموعه ١١) على طاولة الكرابس. كم رمية، في المتوسط، أحتاج لملاحظة ذلك؟

Ace2

41,660,902,667,961,039,785,742 لفة.

وهنا الحل الخاص بي (PDF).

يتم رمي زوج من النرد العادل ذي الستة أوجه مرارًا وتكرارًا حتى يحدث أحد الحدثين التاليين:

أ) مجموع العدد الناتج هو 12.
ب) يتم الحصول على مجموع 7 مرتين متتاليتين.

ما هو الأرجح أن يحدث أولا؟

مجهول

المجموع 12.

[spoiler=الحل]

يترك:

  • p = احتمال الحصول على الرقم 12 أولاً من الحالة الأولية أو في أي وقت لم تكن فيه الرمية السابقة 7.
  • س = احتمال ظهور الرقم 12 أولاً عندما كانت الرمية السابقة هي 7.

وهذا ما يُعرف بمشكلة سلسلة ماركوف.

قبل أن نصل إلى ذلك، تذكر أن احتمال الحصول على مجموع 7 هو 1/6، واحتمال الحصول على مجموع 12 هو 1/36.

يمكننا تعريف p و q من حيث بعضهما البعض، على النحو التالي:

  • (1) ص = (1/36) + (6/36)س + (29/36)ص
  • (2) س = (1/36) + (29/36)ص

دعونا نضرب المعادلة (1) في 36:

36p = 1 + 6q + 29p
(3) 7p = 1 + 6q

دعونا نستبدل قيمة q في (2) في (3):

7ع = 1 + 6*((1/36) + (29/36)ع)
7p = 1 + (1/6) + (29/6)p
42 بنسًا = 6 + 1 + 29 بنسًا
13 ب = 7
س = 7/13

لذا، فإن احتمال الحصول على الرقم 12 أولاً هو 7/13 =~ 53.85%.

وبالتالي فإن احتمال الحصول على الرقم 7 مرتين متتاليتين أولاً هو 46.15%.

وبالتالي، فمن الأرجح أن يتم الحصول على المجموع 12 أولاً.