احتمال - الألغاز
أرغب في معرفة بعض المعلومات الدقيقة حول احتمالات رمي النرد. إذا كان لديك ستة أحجار نرد ورميتها دفعة واحدة، فإن احتمال ظهور جميعها برقم واحد هو 1 من 46,656. سؤالي هو: ما هي احتمالات ظهور رقم واحد مقابل خمسة أرقام؟ أنا مهتم حقًا بمعرفة الصيغة التي يجب استخدامها لحساب هذا النوع من المسائل.
احتمال ظهور س من الآحاد من أصل ص نرد هو combin(y,x)*(1/6) x *(5/6) yx . راجع قسمي حول الاحتمالات في البوكر لشرح دالة combin(x,y). على سبيل المثال، احتمال ظهور أربعة آحاد هو combin(6,4)*(1/6) 4 *(5/6) 2 = 0.803755%.
عدد الآحاد في ستة أحجار نرد
| تلك | احتمال |
|---|---|
| 0 | 0.3348980 |
| 1 | 0.4018776 |
| 2 | 0.2009388 |
| 3 | 0.0535837 |
| 4 | 0.0080376 |
| 5 | 0.0006430 |
| 6 | 0.0000214 |
| المجموع | 1.0000000 |
ذهب ثمانية لاعبين غولف إلى ملعب جديد. وضع مساعد الكادي ثماني حقائب على أربع عربات عشوائيًا. وضع اللاعبون ثماني كرات غولف مُعلّمة في قبعة. رُميت الكرات في الهواء. الكرتان الأقرب من بعضهما كانتا شريكتين. في كل مرة، كانت حقائب غولف الشريكين على العربة نفسها. ما احتمال أن تكون حقائب الغولف قد وُضعت بشكل صحيح قبل الرمية؟
الحل النموذجي لعدد التركيبات هو: combin(8,2)*combin(6,2)*combin(4,2)/fact(4) = 25*15*6/24 = 105. طريقة أخرى لحل عدد التركيبات هي اختيار لاعب غولف عشوائيًا. هناك 7 لاعبين محتملين لمقارنته بهم. ثم نختار لاعب غولف آخر عشوائيًا من بين اللاعبين الستة المتبقين. هناك 5 لاعبين محتملين لمقارنته بهم. ثم نختار لاعب غولف آخر عشوائيًا من بين اللاعبين الأربعة المتبقين. هناك 3 لاعبين محتملين لمقارنته بهم. إذن، عدد التركيبات هو 7*5*3 = 105. وبالتالي، فإن الإجابة هي 1 من 105.
لقد أرسل لي أحد الأصدقاء هذا ، كنت أتساءل عما إذا كانت هناك صيغة لكيفية عمل هذا.
غالبًا ما تنجح ألغاز قراءة العقول هذه نظرًا لغرابة رياضية مثيرة للاهتمام. إذا كان مجموع أرقام أي عدد قابلًا للقسمة على 9، فإن العدد نفسه قابل للقسمة على 9. لنجرب ذلك على رقم هاتف مطعم لاس فيغاس تروبيكانا (702-739-2222). مجموع الأرقام هو 7+0+2+7+3+9+2+2+2+2 = 36. العدد 36 قابل للقسمة على 9 بالتساوي، لذا يجب أن يكون العدد 702739222 قابلًا للقسمة على 9 أيضًا. إليك دليل على ذلك.
- ليكن n أي عدد صحيح. عبّر عن n بـ d 0 *1 + d 1 *10 + d 2 *100+ d 3 *1000+ ... + d n *10 n ، حيث d n هو الرقم الأول، وd n-1 هو الرقم الثاني، وهكذا.
- n = [d 0 + d 1 + d 2 + ... + d n ] + [d 1 *9 + d 2 *99+ d 3 *999+ ...+ d n *999...9 (عدد يحتوي على n تسعات)]
- n = [d 0 + d 1 + d 2 + ... + d n ] + 9*[d 1 *1 + d 2 *11+ d 3 *111+ ... d n *111...1 (عدد يحتوي على n واحد)]
- 9*أي عدد صحيح قابل للقسمة بالتساوي على 9. لذا، إذا كان d 0 + d 2 + d 2 + ... + d n ، أو مجموع الأرقام، قابلاً للقسمة على 9، فيجب أن يكون العدد بأكمله قابلاً للقسمة على 9.
بعد أن انتهينا من هذا البرهان، يُمكننا النظر في هذه الخدعة السحرية. تطلب المسألة منك اختيار أي رقم. ثم إعادة ترتيب الأرقام لتكوين رقم ثانٍ. ثم طرح الرقم الأصغر من الرقم الأكبر.
الإجابة ستكون دائمًا مجموع أرقام قابلة للقسمة على 9. لماذا؟ لكل رقم في العدد الأصلي، يظهر في مكان آخر في العدد الآخر. بتقسيم مجموعة أرقام واحدة في كل مرة، مع تغيير جميع الأرقام الأخرى إلى صفر، يمكننا تلخيص كل مجموعة على النحو التالي: +/- n*[10 x - 10 y ] (حيث x>=y وn هو الرقم) = +/- n *10 y * (10 xy - 1) = 10 y * (عدد مكون من تسعة فقط) = عدد قابل للقسمة على 9.
لنلقِ نظرة على مثال. لنفترض أن العدد الأصلي هو ١٩٦٥. حوّله إلى ٦٩٥١. ٦٩٥١ - ١٩٦٥ = ٦*(١٠٠٠-١٠) + ٩*(١٠٠-١٠٠) + ٥*(١٠-١) + ١*(١-١٠٠٠) = ٦*٩٩٠ + ٩*٠ + ٥*٩ + ٦*-٩٩٩. لاحظ أن كل جزء قابل للقسمة على ٩، وبالتالي فإن العدد الناتج بعد الطرح يجب أن يكون قابلًا للقسمة على ٩ أيضًا، وأخيرًا، مجموع الأرقام قابل للقسمة على ٩ أيضًا.
تطلب منك الخدعة بعد ذلك وضع دائرة حول رقم ما عدا 0، ثم إدخال مجموع جميع الأرقام الأخرى. سيحتاج البرنامج بعد ذلك فقط إلى إضافة رقم إلى الرقم الذي أدخلته، ليصبح المجموع قابلاً للقسمة على 9. على سبيل المثال، إذا قلت إن مجموع أرقامك هو 13، فلا بد أنك وضعت دائرة حول الرقم 5، لأن 13 + 5 = عدد قابل للقسمة على 9.
السبب في عدم قدرتك على وضع دائرة حول الصفر هو أنه إذا قمت بذلك ثم أدخلت رقمًا قابلًا للقسمة على 9، فلن يعرف البرنامج ما إذا كنت قد وضعت دائرة حول 0 أو 9.
موقع رائع. أشير إليه كثيرًا بصفتي مُقامرًا مهتمًا بالاحتمالات والإحصاء، لكن هذا السؤال يتعلق في الواقع بعملي. يُصرّ قسم الموارد البشرية على أن أُقيّم فريقي الصغير (خمسة أشخاص) على منحنى تصاعدي - واحد من أعلى 5% من جميع الموظفين، وواحد من الـ 20% التالية، وواحد من الـ 50% التالية، وواحد من الـ 20% التالية، وواحد من أدنى 5%. لدى الشركة حوالي 5000 موظف. ما احتمال أن ينطبق هذا التوزيع على عينة صغيرة كهذه؟
شكرًا على الثناء. هذه مسألة جيدة. احتمال أن يكون موظف واحد فقط ضمن أدنى ٥٪ هو ٥*(٠.٠٥)*(٠.٩٥) ٤ = ٠.٢٠٣٦٢٧. بما أن أحد الموظفين ضمن أدنى ٥٪، فإن احتمال أن يكون موظف واحد فقط ضمن الـ ٢٠٪ التالية هو ٤*(٠.٢/٠.٩٥)*(٠.٧٥/٠.٩٥) ٣ = ٠.٤١٤٣٦١. بما أن هذين الموظفين ذوي التحصيل المتدني، فإن احتمال أن يكون موظف واحد فقط ضمن الـ ٥٠٪ التالية من أصل الـ ٧٥٪ المتبقية هو ٣*(٠.٥/٠.٧٥)*(٠.٢٥/٠.٧٥) ٢ = ٠.٢٢٢٢٢٢. احتمال أن يكون أحد الموظفين المتبقيين ضمن أدنى ٢٠٪ من الـ ٢٥٪ هو ٢*(٠.٢/٠.٢٥)*(٠.٠٥/٠.٢٥) = ٠.٣٢. إذا أخذنا حاصل ضرب كل هذه الاحتمالات، نحصل على 0.006، أو 3/5 من 1%.
إلى صاحب السؤال حول إحصاءات الطلبات ( العمود رقم ١٠٠ )، لديّ اعتراضان: أحدهما صغير والآخر كبير. فشلت طريقتك في إجراء تصحيح لعدد محدود من الموظفين، وهو أمرٌ أعترف بأنه بسيطٌ جدًا مع ٥٠٠٠ موظف، ولكنه بالتأكيد لم يكن ليكون كذلك لو كان عدد الموظفين ٢٠ موظفًا!
والأهم من ذلك، أنك تفترض ضمنيًا أن المديرين لا يؤثرون على موظفيهم. لنفترض أن المديرين الجيدين، من خلال التوظيف والفصل المدروس، أو من خلال مهارات تحفيزية تفوق المتوسط، يرفعون المستوى المتوسط لموظفيهم. دون مراعاة هذا التأثير، سنميل إلى زيادة أو نقصان الاحتمالات الناتجة. أنا متأكد من أنك تعلم هذا، لكنني حساس له لأنني أجري الكثير من الحسابات المشابهة في قضايا التمييز، وعدم التكيف مع العوامل التي يمكننا التكيف معها (في هذه الحالة، تأثير خاص بالمجموعة) غالبًا ما يُضلّل الناس.
شكراً على هذه النقاط الجيدة. مع ذلك، فإن البديل لعدم التحكم في توزيع تقييمات الأداء الوظيفي هو تضخيم التقييمات. سيُجبر المدير على إصدار تقييمات مبالغ فيها لإرضاء موظفيه. بصفتي موظفاً حكومياً لعشر سنوات، أتحدث عن هذا الأمر من واقع خبرتي. عندما درّست في جامعة نيفادا، لاس فيغاس، لم يكن هناك معيار لمعدل التراكمي المتوسط للفصل الدراسي، ولكن كانت هناك توقعات معينة حول شكل منحنى التقييم في نهاية الفصل الدراسي. على الأقل في بيئة جامعية، اعتقدت أن ذلك يُمثل سياسة معقولة. ربما في بيئة الأعمال، يكون من الأفضل أيضاً استخدام وسيلة منطقية.
هل توجد أي مسائل شهيرة لم تُحل بعد تواجه رياضيات الألعاب؟ مثل نظرية فيرما الأخيرة في عالم المقامرة. إذا كان الأمر كذلك، هل يمكنك مشاركة مثال؟
سؤال جيد. لا أستطيع التفكير في أي شيء.
كيف يعمل هذا: www.1800gotjunk.com/genie/ ؟
لنُعبّر عن عددك بـ ١٠ط + ع. يُطلب منك طرح كل رقم، ليتبقى لديك ١٠ط + ع = ٩ط، وهو عدد قابل للقسمة على ٩. لاحظ أن جميع الأعداد القابلة للقسمة على ٩ تحتوي على نفس العنصر، وهو العنصر الذي تنبأ به الجني.
سأخوض امتحان ترخيص مزاولة المهنة قريبًا. تنص اللوائح على ما يلي:
- يتكون الامتحان من 7 مواد.
- بالنسبة لكل مادة، سيتم طرح 60 سؤالاً من نوع الاختيار من متعدد.
- يجب أن يكون لكل سؤال اختيار من متعدد أربع إجابات محتملة، ولكن إجابة واحدة صحيحة فقط.
- من أجل النجاح، يجب على المتقدم للامتحان الحصول على معدل عام لا يقل عن 75% ويجب ألا يقل معدله في أي مادة عن 65%.
سؤالي هو: إذا خمن الممتحن جميع إجاباته، فما هي فرصته في النجاح؟ بمعنى آخر، ما هو احتمال النجاح بالصدفة؟
لتحقيق شرط 75%، يجب على الطالب الإجابة على 315 سؤالاً على الأقل من أصل 420 سؤالاً بشكل صحيح. العدد المتوقع للإجابات الصحيحة من التخمين هو 420 × 0.25 = 105. الانحراف المعياري هو (420 × 0.25 × 0.75) ^ 0.5 = 8.87412. لذا، يجب على المرشح تجاوز التوقعات بـ 210 أسئلة، أو 210 / 8.87412 = 23.66432 انحرافًا معياريًا. احتمالية حدوث ذلك عالية جدًا. لو خضع كل كائن حي على الأرض لهذا الاختبار، وأجاب عشوائيًا، لأشك في نجاح أي شخص أو أي شيء. لن أتطرق حتى إلى الشرط الآخر.
إذا كان لدى فريق كرة القدم في الجامعة فرصة 10% للفوز بالمباراة الأولى وفرصة 30% للفوز بالمباراة الثانية وفرصة 65% لخسارة المباراتين، فما هي فرصهم في الفوز مرة واحدة بالضبط؟
إذا افترضنا أن المباراتين مستقلتان، فإن احتمال خسارة المباراتين سيكون 90% × 70% = 63%. ولكن بما أنك تقول إن احتمال خسارة المباراتين هو 65% (وهو أعلى من 63%)، فهذا يعني أن الحدثين مترابطان. إذا كان احتمال خسارة المباراتين 65%، وخسارة المباراة الثانية فقط 70%، فإن احتمال الفوز في المباراتين 1 و2 يجب أن يكون 5%. وبنفس المنطق، فإن احتمال خسارة المباراتين 25%. هذا يبقي 5% فقط للفوز في المباراتين. لذا، فإن احتمال الفوز مرة واحدة فقط هو 25% + 5% = 30%.
في برنامج المسابقات "لنعقد صفقة"، هناك ثلاثة أبواب. على سبيل المثال، لنفترض أن بابين يكشفان عن ماعز، وواحد يكشف عن سيارة جديدة. يختار مقدم البرنامج، مونتي هول، متسابقين لاختيار باب. في كل مرة يفتح مونتي بابًا يكشف عن ماعز أولاً. لنفترض هذه المرة أنه يخص المتسابق الأول. مع أن مونتي لم يفعل ذلك، ماذا لو عرض مونتي على المتسابق الآخر فرصة تغيير الباب في هذه المرحلة، إلى الباب الآخر غير المفتوح. هل يجب عليه تغيير الباب؟
نعم! يكمن سر هذه المشكلة في أن المُضيف مُقدّرٌ له أن يفتح بابًا فيه عنزة. إنه يعرف أي باب فيه السيارة، لذا بغض النظر عن الأبواب التي يختارها اللاعبون، يمكنه دائمًا الكشف عن عنزة أولًا. يُعرف هذا السؤال باسم "مفارقة مونتي هول". يعود جزء كبير من الالتباس حوله إلى أنه غالبًا ما يُساء تفسير السؤال عند صياغته، حيث يُغفل المُضيف معرفة مكان السيارة، ويكشف دائمًا عن عنزة أولًا. أعتقد أن بعض اللوم يقع على مارلين فوس سافانت ، التي أساءت صياغة السؤال في عمودها. لنفترض أن الجائزة خلف الباب رقم 1. فيما يلي ما سيحدث إذا اتبع اللاعب (المتسابق الثاني) استراتيجية عدم التبديل.
- يختار اللاعب الباب 1 --> يفوز اللاعب
- يختار اللاعب الباب 2 --> يخسر اللاعب
- يختار اللاعب الباب رقم 3 --> ويخسر اللاعب
فيما يلي ما قد يحدث إذا كان لدى اللاعب استراتيجية للتبديل.
- يختار اللاعب الباب 1 --> يكشف المضيف عن الماعز خلف الباب 2 أو 3 --> ينتقل اللاعب إلى باب آخر --> يخسر اللاعب
- يختار اللاعب الباب 2 --> يكشف المضيف عن الماعز خلف الباب 3 --> ينتقل اللاعب إلى الباب 1 --> يفوز اللاعب
- يختار اللاعب الباب 3 --> يكشف المضيف عن الماعز خلف الباب 2 --> ينتقل اللاعب إلى الباب 1 --> يفوز اللاعب
لذا، بعدم تغيير اللاعب، تكون فرص فوزه 1/3. أما بتغييره، فتصبح فرص فوزه 2/3. لذا، يجب على اللاعب تغييره بالتأكيد.
لمزيد من القراءة عن مفارقة مونتي هول، أنصحك بقراءة المقال على ويكيبيديا .
لا أتفق مع إجابتك على سؤال مونتي هول في عمود ١٩ نوفمبر ٢٠٠٤. بافتراض أن السيارة خلف الباب الأول، هناك أربعة احتمالات، وهي أن تكون الجائزة خلف الباب الأول.
- يختار اللاعب الباب 1 --> المعروض 2 --> ينتقل إلى الباب 3 ويخسر
- يختار اللاعب الباب 1 --> يظهر 3 --> ينتقل إلى 2 ويخسر
- يختار اللاعب الباب 2 --> يظهر 3 --> التبديل إلى 1 والفوز
- يختار اللاعب الباب 3 --> يظهر 2 --> التبديل إلى 1 والفوز
كما ترى، احتمال الفوز ٥٠٪ سواءً غيّرت اللعبة أم لا. علاوة على ذلك، فإنّ القول إنّ التغيير سيكون أفضل يتعارض مع المنطق.
خطأك هو افتراض أن احتمالية وقوع كلٍّ من هذه الأحداث هي ٢٥٪. فيما يلي الاحتمالية الصحيحة لكل حدث.
- يختار اللاعب الباب 1 (1/3) * الموضح 2 (1/2) = يخسر اللاعب (1/6)
- يختار اللاعب الباب 1 (1/3) * يظهر 3 (1/2) = يخسر اللاعب (1/6)
- يختار اللاعب الباب 2 (1/3) * الموضح 3 (1/1) = يفوز اللاعب (1/3)
- يختار اللاعب الباب 3 (1/3) * الموضح 2 (1/1) = يفوز اللاعب (1/3)
وبالتالي فإن الأحداث الخاسرة لها إجمالي احتمال 2*(1/6) = 1/3 والأحداث الفائزة لها إجمالي احتمال 2*(1/3)=2/3.
مع وجود خمس إضافات مختلفة للاختيار من بينها، كم عدد أنواع البيتزا المختلفة التي يمكنك صنعها، بأي عدد من الإضافات؟
هناك طريقة واحدة بدون إضافات، و٥ طرق بإضافة واحدة، و١٠ طرق بإضافة إضافتين، و١٠ طرق بثلاث إضافات، و٥ طرق بأربع إضافات، وطريقة واحدة بخمس إضافات. إذن، الإجابة هي ١ + ٥ + ١٠ + ١٠ + ٥ + ١ = ٣٢. طريقة أخرى للحل هي إما استخدام الإضافات أو عدم استخدامها. إذن، المجموع ٢ = ٥ = ٣٢.
قرأتُ في الصحيفة الأسبوع الماضي أن الزلزال الأخير الذي ضرب إندونيسيا ضربها في 26 ديسمبر. كما أظهرت أن من بين أخطر ثمانية زلازل ضربت البلاد خلال المئة عام الماضية، وقع ثلاثة منها في 26 ديسمبر. كنتُ أتساءل عن احتمال وقوع ثلاثة زلازل ضخمة في اليوم نفسه، مع العلم أن هذه الحقائق: الزلازل بهذا القدر (8.0 أو أكثر) تحدث مرة واحدة فقط سنويًا. وقع آخر زلزال كبير قبل عام واحد بالضبط، في 26 ديسمبر 2003 في إيران (هل هناك احتمالات متتاليتان؟). أتطلع إلى سماع أخبارك.
بعد اكتشافي أن الادعاء بأن أعاصير فلوريدا ضربت فقط مقاطعات بوش الانتخابية كان مجرد خدعة (انظر مقال ١٧ أكتوبر ٢٠٠٤ )، سأصبح أكثر تشككًا في هذه المصادفات المزعومة. فوفقًا للمركز الوطني لمعلومات الزلازل، من بين أقوى ١١ زلزالًا منذ عام ١٩٩٠، فإن الزلزال الأخير الذي حدث عام ٢٠٠٤ ضرب المنطقة في ٢٦ ديسمبر. أما الزلزال الإيراني الذي ذكرته، فقد بلغت قوته ٦.٧ درجة فقط، وهو بعيد كل البعد عن أن يكون ضمن قائمة الزلازل الثمانية الأوائل.
بكم تبدأ إذا بعت نصف البيضة ونصف بيضة كل يوم؛ وبعد ثلاثة أيام، لم يعد لديك بيض؟ في نهاية كل يوم، يكون عدد البيض عددًا صحيحًا.
لنفترض أن d (للنهار) هو عدد البيض في بداية النهار، وn (للليل) هو عدد البيض في نهايته. تخبرنا المسألة أن d/2 - ? = n. لذا، لنحل d بدلالة n.
د/2 = ن + ؟
د= 2ن + 1
ففي اليوم الثالث n=0، وبالتالي d=1.
في اليوم الثاني n=1، لذا d=3.
في اليوم الثالث n=3، لذا d=7.
إذن لديك الآن، لقد بدأت بـ 7 بيضات.
تخيل جزيرة يسكنها عشرة أشخاص، والسياسة المتبعة هي اختيار أحد سكانها عشوائيًا كل يوم ليكون زعيمًا لمدة يوم واحد فقط؛ وبعد انقضاء اليوم، يُختار آخر عشوائيًا (أي أن نفس الشخص الذي كان زعيمًا للتو لديه فرصة 1/10 ليصبح زعيمًا مرة أخرى). السؤال المطروح: كم يومًا يجب أن ينقضي في المتوسط قبل أن يصبح كل فرد من سكان الجزيرة زعيمًا مرة واحدة على الأقل؟
سيستغرق الأمر يومًا واحدًا فقط ليتولى شخص واحد منصب الرئيس. في اليوم الثاني، يكون احتمال تولي رئيس جديد 0.9. عدد الأيام المتوقع لتولي رئيس جديد، إذا كان احتمال كل يوم 0.9، هو 1/0.9 = 1.11. ينطبق هذا على أي احتمال: عدد المحاولات المتوقعة حتى النجاح هو 1/p. لذا، بعد تولي شخصين منصب الرئيس، يكون احتمال تولي رئيس جديد في اليوم التالي 0.8. لذا، فإن فترة انتظار الرئيس الثالث هي 1/0.8 = 1.25 يوم. والإجابة هي مجموع فترات الانتظار، أي 1/1 + 1/0.9 + 1/0.8 + ... + 1/0.1 = 29.28968 يومًا.
نصف قطر الدائرة هو ١. المثلث متساوي الأضلاع. أوجد مساحة كل منطقة ملونة.
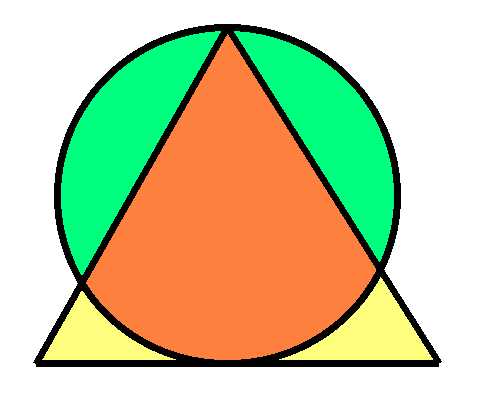
لا أريد أن أفسد الإجابة لمن يريد حلها بنفسه. للإجابة والحل، تفضل بزيارة موقعي الإلكتروني الآخر mathproblems.info ، المسألة ١٨٩.
لنفترض أنك فزت في مسابقة، حيث كان عليك تسديد رمية حرة في الشوط الأول من مباراة NBA، وإذا نجحت فيها، فستربح مليون دولار. علاوة على ذلك، يمكنك الاستمرار في تسديد الرميات الحرة، سواءً مضاعفة أو لا شيء، حتى تُخطئ أو تختار التوقف. إذا كانت نسبة نجاحك في تسديد الرميات الحرة 75%، فمتى ستتوقف؟ وهل ستتوقف أصلًا؟ في مرحلة ما، سيبدأ المال بالتناقص تدريجيًا. ماذا ستفعل؟
في مرحلة ما، يجب عليك رفض رهان جيد لأن المخاطر عالية جدًا. أعتقد شخصيًا أن المقياس الجيد للمتعة التي يحصل عليها المرء من المال هو لوغاريتم المبلغ. لا يهم أساس اللوغاريتم لذا دعنا نستخدم 10. ومع ذلك، لا يمكننا أخذ لوغاريتم أقل من 10، لذا دعنا نقول أن المتعة هي 0 لأي مبلغ أقل من عشرة. لذا في مثالنا، لنفترض أن لديك 0 دولار قبل الفوز بـ 1,000,000 دولار برميتك الأولى. الآن لديك log(1,000,000) = 6 وحدات من السعادة. القيمة المتوقعة لسعادتك عند أخذ رمية حرة أخرى هي 0.75 * log(2,000,000) + 0.25 * 0 = 4.975772. هذا أقل من 6 لذا في هذه الحالة يجب أن تأخذ المليون وتمشي. ومع ذلك، قد يكون الأمر مختلفًا إذا كان لديك بالفعل بعض المال. لنفترض أن لديك بالفعل 200,000 دولار. إذن، سعادتك بالفوز هي log(1,200,000) = 6.07918. سعادتك بالمخاطرة بالمليون ومحاولة أخرى هي 0.75*log(2,200,000) + 0.25*log(200,000) = 6.082075، أي أنك ستخوض المحاولة الثانية بفارق ضئيل. إذا فزت في تلك المحاولة، فسيكون خيارك بين log(2,200,000) = 6.34242 و0.75*log(4,200,000)+0.25*log(200,000) = 6.29269. في هذه الحالة، يجب ألا تخوض المحاولة الثالثة، بل تفوز بـ 2,000,000 دولار. نقطة التعادل لقبول الرهان المزدوج الأول هي ثروة موجودة قدرها 191,487 دولارًا. لقبول الرهانين المزدوجين، يجب أن يكون لديك 382,975 دولارًا من أموالك الأخرى.
أتذكر أنه إذا كان هناك 22 شخصًا في غرفة، فإن احتمالية احتفال اثنين منهم بنفس عيد الميلاد متساوية (الشهر واليوم، وليس السنة). لقد نسيتُ كيفية إجراء عملية حسابية لإثبات ذلك. هل يمكنك تزويدي بها من فضلك؟
أعتقد أنني أجبتُ على هذا السؤال سابقًا، لكن احتمالية ٥٠/٥٠ أقرب إلى ٢٣. لتبسيط الأمور، لنتجاهل السنوات الكبيسة. الإجابة الأطول هي ترتيب الأشخاص الـ ٢٣ بطريقة ما. احتمال أن يكون تاريخ ميلاد الشخص الثاني مختلفًا عن تاريخ ميلاد الشخص الأول هو ٣٦٤/٣٦٥. احتمال أن يكون تاريخ ميلاد الشخص الثالث مختلفًا عن تاريخ ميلاد الشخصين الأول والثاني، بافتراض اختلافهما، هو ٣٦٣/٣٦٥. استمر في التكرار حتى يصل الشخص ٢٣. بالتالي، الاحتمال هو (٣٦٤/٣٦٥)*(٣٦٣/٣٦٥)*...*(٣٤٣/٣٦٥) = ٤٩٫٢٧٠٣٪. لذا، فإن احتمال عدم وجود تطابق هو ٤٩٫٢٧٪، واحتمال وجود تطابق واحد على الأقل هو ٥٠٫٧٣٪. الحل الآخر هو عدد التباديل لـ 23 عيد ميلاد مختلف مقسومًا على العدد الإجمالي للطرق لاختيار 23 رقمًا عشوائيًا من 1 إلى 365، وهو التباديل (365، 23) / 365 23 = 42،200،819،302،092،400،000،000،000،000،000،000،000،000،000،000،000،000،000،000،000 / 85،651،679،353،150،300،000،000،000،000،000،000،000،000،000،000،000،000،000،000،000 = 49.27٪.
تُوزّع رواتب المعلمين الأسبوعية في إحدى الولايات توزيعًا طبيعيًا بمتوسط حسابي قدره 490 دولارًا وانحراف معياري قدره 45 دولارًا. ما احتمال أن يتقاضى معلم مُختار عشوائيًا أكثر من 525 دولارًا أسبوعيًا؟ لا أتذكر كيفية حساب الاحتمالية من المتوسط الحسابي والانحراف المعياري فقط دون حساب عدد السكان.
سيكون ذلك أعلى من المتوسط بمقدار 35 دولارًا، أو 7/9 انحراف معياري. احتمالية تجاوز التوقعات بأكثر من 7/9 انحراف معياري هي 1-Z(7/9) = 1- 0.78165 = 0.21835.
يلعب شخصان لعبة "حجرة ورقة مقص". يُفترض أن اللعبة لا تتضمن أي استراتيجية. إذا كنتما تلعبان "أفضل من 3"، وفاز اللاعب "أ" بالجولة الأولى، فما احتمالات فوز اللاعب "ب"؟
سيحتاج اللاعب B إلى الفوز بالمباراتين التاليتين (دون احتساب التعادلات)، لذا فإن الاحتمال هو (1/2)*(1/2) = 1/4.
مرحباً، أردتُ أن أسألك هذا السؤال لأنني لا أجده على الإنترنت. آمل أن تجيبني عليه: ما هي احتمالات وجودنا؟ سواءً على الأرض أو في أي مكان آخر في الكون؟ إنه ليس سؤالاً مُقامرة، بل إجابة يجب أن نعرفها جميعاً لنُدرك مدى احتمالات تفوقنا بمجرد البقاء على قيد الحياة!
أعتقد أن احتمال وجود حياة ذكية في أي مكان من المجرة كبير جدًا. تسعى معادلة دريك إلى تقدير عدد حالات الحياة الذكية في المجرة، والتي بناءً على الأرقام التي تُدخلها، تصل إلى رقم يقارب المليون. مع ذلك، لا يوجد دليل قاطع على أن هذه الحضارات قد زارتنا أو تواصلت معنا. لذا، فإن سؤال فيرمي الشهير هو "أين الجميع؟". أعتقد أن نقص الأدلة على وجود حياة ذكية أخرى يُلقي بعض الشك على معادلة دريك، لكنني ما زلت أضع عدد الحضارات الذكية في مجرتنا في حدود الألف. هذه مجرد مجرتنا، فهناك مليارات المجرات. ومع ذلك، فالمسافة بين المجرات شاسعة جدًا، فلا جدوى من مناقشة السفر أو التواصل بينها. لذا، للإجابة على سؤالك، أقول إن النسبة 99.9% تقريبًا.
لنفترض أن فندقًا يضم ١٠ ملايين غرفة و١٠ ملايين مفتاح إلكتروني. بسبب خطأ حاسوبي، تمت برمجة كل مفتاح برمز عشوائي، مع احتمالية صحة واحد من ١٠ ملايين. الفندق مباع بالكامل. ما احتمال أن يكون لدى عميل واحد على الأقل مفتاح صالح؟
الإجابة الدقيقة هي: 1-(9,999,999/10,000,000) 10,000,000 = 0.632121. وهذا يُعادل أيضًا (e-1)/e لأقرب سبعة منازل عشرية.
يوجد في الامتحان 75 سؤالاً من نوع الاختيار من متعدد. يحتوي كل سؤال على 4 إجابات محتملة، واحدة منها فقط صحيحة. درجة النجاح في الامتحان هي 50%. ما هي احتمالات النجاح بتخمين كل إجابة؟
1 في 635،241.
بالنسبة للمراهنة أثناء اللعب، إذا كان لدى لاعب تنس فرصة "p" للفوز بلعبة، فما هي فرصته للفوز بالمجموعة؟
حسب فهمي لقواعد التنس، الفائز بالمجموعة هو أول من يفوز بستة أشواط، وبفارق شوطين على الأقل، إلا أن التعادل 6-6 يؤدي إلى شوط كسر التعادل. يوضح الجدول التالي احتمالية الفوز بالمجموعة، مضافًا إليها احتمالية الفوز بشوط.
الاحتمالات في التنس
| احتمال فوز اللعبة | احتمال مجموعة الفوز |
| 0.05 | 0.000003 |
| 0.1 | 0.000189 |
| 0.15 | 0.001899 |
| 0.2 | 0.009117 |
| 0.25 | 0.028853 |
| 0.3 | 0.06958 |
| 0.35 | 0.138203 |
| 0.4 | 0.23687 |
| 0.45 | 0.361085 |
| 0.5 | 0.5 |
| 0.55 | 0.638915 |
| 0.6 | 0.76313 |
| 0.65 | 0.861797 |
| 0.7 | 0.93042 |
| 0.75 | 0.971147 |
| 0.8 | 0.990883 |
| 0.85 | 0.998101 |
| 0.9 | 0.999811 |
| 0.95 | 0.999997 |
صيغة أي احتمال للفوز في لعبة p، وخسارة q، هي 1*p 6 + 6*p 6 *q + 21*p 6 *q 2 + 56*p 6 *q 3 + 126*p 6 *q 4 + 252*p 7 *q 5 + 504*p 7 *q 6
أنت في قاربٍ مع صخرة، على بحيرةٍ عذبة. ألقيتَ الصخرة في البحيرة. بالنسبة لليابسة (الشاطئ)، هل يرتفع منسوب المياه، أم ينخفض، أم يبقى ثابتًا؟ يعتقد زملائي أن منسوب المياه سيبقى ثابتًا.
سينخفض منسوب المياه بالنسبة للشاطئ. داخل القارب، تضغط الصخرة على الزورق، مما يدفع الماء حوله لأعلى. كمية الماء المُزاحة تساوي وزن الصخرة. على سبيل المثال، صخرة تزن 10 أرطال ستُزاح 10 أرطال من الماء لأعلى. عند رمي الصخرة في البحر، لن يكون الوزن هو المهم، بل حجم الصخرة. لذا، ستدفع الصخرة كمية من الماء تساوي حجم الصخرة لأعلى. كتلة الصخرة أكبر من كتلة الماء، لذا تُزاح الصخرة كمية من الماء تُضغط عليها لأسفل أكثر مما تُزاح داخلها. لذا، سيكون مستوى البحيرة أعلى مع وجود الصخرة في الزورق منه في قاع البحيرة.
كيف يعمل هذا؟
- احصل على آلة حاسبة. (لن تتمكن من القيام بذلك في رأسك)
- أدخل الأرقام الثلاثة الأولى من رقم هاتفك (ليس رمز المنطقة)
- اضرب في 80
- أضف 1
- اضرب في 250
- أضف آخر 4 أرقام من رقم هاتفك
- أضف آخر 4 أرقام من رقم هاتفك مرة أخرى.
- اطرح 250
- قسمة العدد على 2
هل تعرف الجواب؟
لنسمِّ أول ثلاثة أرقام من رقم هاتفك x، وآخر أربعة أرقام y. والآن، لنرَ ما توصلتُ إليه في كل خطوة.
- مستعد!
- إكس
- 80x
- 80x+1
- 250*(80x+1) = 20000x+250
- 20000x+250+y
- 20000x+250+2y
- 20000س+250+2ص-250 = 20000س+2ص
- (20000x+2y)/2 = 10000x+y
هذا بالطبع يساوي رقم هاتفك. نحتاج إلى 10000x لنقل البادئة أربعة خانات إلى اليسار، ثم نضيف آخر أربعة أرقام.
هناك سحب على سيارة بقيمة ٢٧,٠٠٠ دولار أمريكي، وست تذاكر تُباع بواقع ٥٠٠ دولار أمريكي لكل ست تذاكر، أو ١٠٠ دولار أمريكي لكل تذكرة. بيعت ٦٨ تذكرة، وغدًا هو الموعد النهائي للشراء. أعلم أنه لتحقيق نسبة فوز ٥٠٪، يجب أن أنفق ٥٦٦٦.٤٤ دولارًا أمريكيًا، ولنسبة فوز ٦٦.٦٦٪، يجب أن أنفق ١١,٣٣٢.٨٨ دولارًا أمريكيًا (صحيح؟). كم يجب أن أنفق (أو كم تذكرة يجب أن أشتري) لأضمن عمليًا الفوز بالسيارة؟ (٩٠٪؟ ٩٥٪؟) هل يستحق هذا السحب المشاركة فيه، أم يجب أن أنفق ثمن السيارة؟
أنت مُحق بشأن احتمالات النصف والثلث. إذا اشتريتَ عددًا من التذاكر، فإن احتمال فوزك هو t/(68+t). لذا، للحصول على احتمال 90%، حَلّ قيمة t كما يلي.
0.9 = t/(68+t)
0.9*(68+t) = t
61.2 = 0.1 طن
t = 612، أو 51000 دولار
لـ 95%...
0.95= ت/(68+ت)
0.95(68+t) = t
64.6 = 0.05 طن
t = 1292، أو 107,666.67 دولارًا
إذا افترضنا أن قيمة السيارة بالنسبة لك هي 27000 دولار، فيجب عليك التوقف عن شراء التذاكر بمجرد أن لا تزيد التذكرة التالية المباعة من احتمالية فوزك بما يكفي لضمان السعر.
لكي تكون التذكرة تستحق السعر، يجب أن تزيد احتمالية فوزك بمقدار p، حيث...
27000*ص=(500/6)
ص=0.003086
لنفترض أن t هو عدد التذاكر التي اشتريتها حيث أنك غير مبالٍ بشراء تذكرة أخرى.
[(t+1)/(t+68+1)] − [t/(t+68)] = 0.003086
[(t+1)/(t+69)] − [t/(t+68)] = 0.003086
[((t+1)*(t+68))/((t+69)*(t+68))] − [(t*(t+69))/((t+68)*(t+69))] = 0.003086
[((t 2 +69t+68)/((t+69)*(t+68))] − [(t 2 +69t)/((t+68)*(t+69))] = 0.003086
68/((ت+68)*(ت+69)) = 0.003086
((ت+68)*(ت+69)) = 220.32
t 2 +137t +4692 = 22032
t 2 +137t - 17340=0
t=(-137+/-(137 2 -4*1*-17340) 2 )/2
ت = 79.9326
دعنا نختبر ذلك عن طريق إدخال بعض القيم للتذاكر المشتراة، على افتراض أن اللاعب يمكنه دائمًا شراء التذاكر بسعر 500 دولار/6 = 83.33 دولارًا لكل منها.
عند 79 تذكرة، تكون التكلفة 79*(500/6) = 6,583.33 دولار، واحتمال الفوز هو 79/(79+68) = 53.74%، وعائدك المتوقع هو 27,000*0.5374 = 14,510.20 دولار، وربحك المتوقع هو 14,510.20 دولار - 6,583.33 دولار = 7,926.87 دولار.
عند شراء 80 تذكرة، تكون التكلفة 80*(500/6) = 6,666.67 دولارًا، واحتمال الفوز هو 80/(80+68) = 54.04%، وعائدك المتوقع هو 27,000 دولار*0.5405 = 14,594.59 دولارًا، وربحك المتوقع هو 14,594.59 دولارًا - 6,666.67 دولارًا = 7,927.92 دولارًا
عند شراء 81 تذكرة، تكون التكلفة 81*(500/6) = 6,750.00 دولار، واحتمال الفوز هو 81/(81+68) = 54.36%، وعائدك المتوقع هو 27,000*0.5436 = 14,677.85 دولار، وربحك المتوقع هو 14,594.59 دولار - 6,750.00 دولار = 7,927.85 دولار.
وبالتالي، يمكننا أن نرى أن الحد الأقصى المتوقع للفوز يصل إلى 80 تذكرة.
أحاول مقارنة تكلفة استبدال ثلاجة قديمة الآن لتوفير تكاليف الكهرباء، مقابل الانتظار حتى تتلف لاستبدالها. يمكنني حساب مدى رخص تشغيل الثلاجة الجديدة مقارنةً بالثلاجة القديمة: 37 دولارًا سنويًا، هذا سهل. ولكن كيف أحسب تكلفة الثلاجة الجديدة؟ لنفترض أن الثلاجة الجديدة تكلف 425 دولارًا. لا أستطيع القول إن *كل* هذا المبلغ 425 دولارًا هو تكلفة جديدة، لأنني سأضطر إلى استبدال الثلاجة القديمة *يومًا ما*، إن لم يكن الآن، لذا سأدفع تكلفة الثلاجة الجديدة في وقت ما على أي حال. لنفترض أن الثلاجة العادية تدوم 14 عامًا وثلاجتي القديمة عمرها 9 سنوات، لذا إذا استبدلتها الآن، فسأستبدلها في غضون 5 سنوات. حاولتُ إنشاء جدول من عمودين، يُقارن تكلفة الاحتفاظ بالثلاجة الحالية لمدة تسع سنوات ثم استبدالها، بتكلفة استبدالها الآن، لكنني لم أعرف كيفية إجراء مقارنة دقيقة، لأنني لم أكن أعرف إلى أي مدىً من الزمن يجب أن أُراعي التكاليف، ولأن الثلاجات تُستبدل في سنوات مختلفة. كيف أقارن الجدوى الاقتصادية للاستبدال الآن مقابل الاستبدال لاحقًا؟ بالمناسبة، هذا ليس حالتي، لأن ثلاجتي الحالية عمرها على الأرجح ٣٠ عامًا. إنه لصديق.
إذا احتفظت بثلاجتك الحالية، فستكون قد أنفقت خلال خمس سنوات مبلغًا إضافيًا قدره 37 دولارًا × 5 = 185 دولارًا على الكهرباء مقارنةً بثلاجة جديدة. إذا استبدلتها الآن، فستخسر 425 دولارًا، ولكن بافتراض الاستهلاك الخطي بعد خمس سنوات، ستظل قيمتها 425 دولارًا × (9/14) = 273.21 دولارًا. لذا، ستكون قد خسرت 425 دولارًا × (5/14) = 151.79 دولارًا بسبب الاستهلاك. لذا، فإن تكلفة استهلاك الثلاجة الجديدة أقل من تكلفة الكهرباء الإضافية للاحتفاظ بالثلاجة القديمة، لذا أنصح بشراء ثلاجة جديدة الآن.
إذا كان هناك ثلاثة أشخاص، فما هو احتمال أن يكون عيد ميلاد شخصين على الأقل في نفس التاريخ؟
بتجاهل يوم الكبيسة، يكون احتمال أعياد الميلاد الثلاثة المختلفة (364/365)*(363/365) = 0.99179583. لذا، يكون احتمال عيد ميلاد مشترك واحد على الأقل هو 1 - 0.99179583 = 0.00820417.
يوجد خمسة أشخاص في غرفة. ما احتمال أن يكون اثنان منهم على الأقل قد وُلدا في نفس شهر الميلاد؟
لتبسيط الأمور، لنفترض أن احتمال ميلاد كل شخص في كل شهر هو ١/١٢. احتمال ميلاد الأشخاص الخمسة جميعًا في أشهر مختلفة هو (١١/١٢)*(١٠/١٢)*(٩/١٢)*(٨/١٢) = ٠٫٣٨١٩٤٤. لذا، احتمال ميلاد شهر واحد هو ١ - ٠٫٣٨١٩٤٤ = ٠٫٦١٨٠٥٦.
وُضِع علينا تحدٍّ في العمل - لمجرد التسلية، ولم يستطع أحدٌ منا حلّها. يمتلك مزارعٌ خمس مقطورات مليئة بالأغنام. أربعٌ منها تحتوي على أغنام تزن 39 كجم، والمقطورة الخامسة تحتوي على أغنام تزن 40 كجم. جميع الأغنام متطابقة. يذهب المزارع إلى السوق. يريد أن يعرف أيّ المقطورات تحتوي على أغنام تزن 40 كجم، ولا يمكنه استخدام الميزان الكبير إلا مرة واحدة! كيف يفعل ذلك؟ أرجوكم ساعدونا، هذا الأمر يُثير غضبنا جميعًا في مكان عملي - إنه عيادة بيطرية!
الجواب موجود في نهاية العمود.
إجابة سؤال الخروف
خذ خروفًا واحدًا من المقطورة 1، واثنتين من المقطورة 2، وثلاثًا من المقطورة 3، وأربعًا من المقطورة 4، وصفرًا من المقطورة 5. إذا كان وزن جميع الأغنام 39 كجم، فسيكون الوزن الإجمالي 39 × 10 = 390 كجم. ومع ذلك، فإن 0 إلى 4 أغنام أثقل بكيلوجرام واحد. إذا كان الوزن الإجمالي 391، فهناك خروف واحد ثقيل على الميزان؛ وبالتالي يجب أن يكون من المقطورة 1. وبالمثل، إذا كان الوزن الإجمالي 392، فهناك خروفان ثقيلان على الميزان، ويجب أن يكونا من المقطورة 2. وبالمثل، فإن الوزن 393 يعني أن الخروف الثقيل موجود في المقطورة 3، والوزن 394 يعني أن الخروف الثقيل موجود في المقطورة 4، والوزن 390 يعني أن الخروف الثقيل موجود في المقطورة 5.
في طائرة بها 180 مقعدًا، ما هي احتمالات جلوسي بجانب الفتاة الجميلة التي أراها والتي ستكون على نفس الرحلة؟
يعتمد ذلك على عدد المقاعد في المجموعة. تحتوي معظم الرحلات الداخلية على ثلاثة مقاعد على جانبي الممر، ما يُنتج 60 مجموعة بثلاثة مقاعد. بعد جلوس أول راكب، سيكون هناك مقعدان في نفس المجموعة من أصل 179 مقعدًا متبقيًا، لذا فإن احتمالية وجودك في نفس المجموعة هي 2/179 = 1.12%. عندها، لا يُمكنك أن تجلس في المقعد الأوسط. احتمالية وجود الشخص الثالث في المقعد الأوسط هي 1/3. إذن، الإجابة هي (2/179) × (2/3) = 0.74%، أو 1 من 134.25.
ثلاثة منطقيين يلعبون لعبة. على كلٍّ منهم كتابة عدد صحيح موجب سرًّا. المنطقي الذي يكتب أقل عدد صحيح فريد سيفوز بثلاثة دولارات. إذا كان لدى الثلاثة الرقم نفسه، سيفوز كلٌّ منهم بدولار واحد. المنطقيون أنانيون، وكلٌّ منهم يسعى لتعظيم مكاسبه. التواصل ممنوع. ما الاستراتيجية التي سيتبعها كل منطقي؟
ستظهر الإجابة في العمود التالي.
عادةً ما أقول إن هذا خارج نطاق تخصصي. مع ذلك، بصفتي خبيرًا اكتواريًا حكوميًا سابقًا لمدة ثماني سنوات، لديّ معرفة واسعة بالضرائب. بناءً على ما قرأته، يُعرّف معظم دخل وارن بافيت بأنه مكاسب رأسمالية، والتي تخضع لضريبة بنسبة 15% فقط. شئنا أم أبينا، فإن قوانين الضرائب تسمح بذلك. ما حيرني هو سبب دفع سكرتيرته ما يصل إلى 30%. وفقًا لهذا الفيديو ، كان يحسب "ضرائب الرواتب والدخل". من الواضح أنه كان يقصد بـ"ضرائب الرواتب" ضرائب الضمان الاجتماعي والرعاية الطبية. لنرَ إن كان 30% معدل ضريبة فيدرالية إجماليًا معقولًا لسكرتيرته.
في عام ٢٠٠٧، فُرضت ضريبة بنسبة ٣٥٪ على أعلى شريحة ضريبية ، ولكن هذا ينطبق فقط على الدخل الذي يزيد عن ٣٤٩,٧٠٠ دولار أمريكي. أما الدخل حتى تلك النقطة، فيُفرض عليه ضريبة أقل بكثير. لنفترض أن سكرتيرته عزباء، وليس لديها أطفال معالون، وكان راتبها ١٠٠,٠٠٠ دولار أمريكي. أولًا، لنطرح الحد الأدنى من الخصومات. في عام ٢٠٠٧، كان الخصم القياسي للأفراد الذين قدموا إقراراتهم الضريبية ٥,٣٥٠ دولارًا أمريكيًا. وكان الخصم الشخصي ٣,٤٠٠ دولار أمريكي. وبالتالي، يتبقى لدينا ١٠٠,٠٠٠ دولار أمريكي - ٥,٣٥٠ دولارًا أمريكيًا - ٣,٤٠٠ دولار أمريكي = ٩١,٢٥٠ دولارًا أمريكيًا دخلًا خاضعًا لضريبة الدخل. بالنسبة للأفراد الذين قدموا إقراراتهم الضريبية في عام ٢٠٠٧، كان معدل الضريبة ١٠٪ على أول ٧,٨٢٥ دولارًا أمريكيًا من الدخل، ثم ١٥٪ حتى ٣١,٨٥٠ دولارًا أمريكيًا، ثم ٢٥٪ حتى ٧٧,١٠٠ دولارًا أمريكيًا، و٢٨٪ حتى ١٦٠,٨٥٠ دولارًا أمريكيًا. إذن، كانت ضريبة دخلها ستكون = 0.1 × 7,825 دولارًا + 0.15 × (31,850 دولارًا - 7825 دولارًا) + 0.25 × (77,100 دولارًا - 31,850 دولارًا) + 0.28 × (91,250 دولارًا - 77,100 دولارًا) = 19,660.75 دولارًا. هذا يمثل 19.7% فقط من دخلها. جميع افتراضاتي، مثل دخلها، وحالة ملفها الضريبي، وعدم تفصيلها، لم تكن في صالحها، أو دفعت إلى فرض معدل ضريبة أعلى.
لنتناول الآن الضمان الاجتماعي والرعاية الطبية. في عام ٢٠٠٧، كانت ضريبة الضمان الاجتماعي ٦.٢٪، حتى دخل ٩٧,٥٠٠ دولار أمريكي، عند إيقافها تمامًا. كان معدل ضريبة الرعاية الطبية لعام ٢٠٠٧ ١.٤٥٪، دون حد أقصى. لذا، فإن مجموع ضريبة الضمان الاجتماعي والرعاية الطبية الخاصة بها كان ٦.٢٪ × ٩٧,٥٠٠ + ١.٤٥٪ × ١٠٠,٠٠٠ = ٧,٤٩٥ دولارًا أمريكيًا. وباحتساب هذه الضرائب، كان معدل ضريبتها الإجمالي سيكون (١٩,٦٦٠.٧٥ دولارًا أمريكيًا + ٧,٤٩٥ دولارًا أمريكيًا) / ١٠٠,٠٠٠ دولار أمريكي = ٢٧.٢٪. ومع ذلك، ما زلنا نفتقر إلى ٣٠٪ بنسبة ٢.٨٪.
أفضل تخمين لدي هو أنها تفكر أيضًا في حقيقة أنها في النهاية هي التي تدفع ضريبة الضمان الاجتماعي والرعاية الطبية المطابقة لصاحب العمل. بالنسبة لأولئك الذين لا يعرفون، فإن ضرائب الضمان الاجتماعي والرعاية الطبية هي في الواقع ضعف ما يتم خصمه من شيكاتك. يدفع صاحب العمل النصف الآخر. ومع ذلك، فإن البعض، بمن فيهم أنا، قد يجادل بأن الموظف هو الذي يدفع كلاهما في النهاية. إذا لم يكن على صاحب العمل دفع هذه الضريبة، فسيكون لديه المزيد من المال لدفع رواتب موظفيه. من السهل أن تشعر بهذه الطريقة عندما تعمل لحسابك الخاص، مثلي، وعليك دفع كلا الحصتين. إذا ضاعفت ضريبة الضمان الاجتماعي / الأدوية، فإن المعدل الآن هو (19660.75 دولارًا + 2 × 7495 دولارًا) / 100000 دولار = 34.7٪. أفترض أن الفرق بنسبة 4.7٪ يرجع إلى أنها تكسب أقل من 100000 دولار، أو أنها متزوجة، أو لديها معالين، أو تفصل الخصومات، أو مزيج من ذلك.
لن تُطبق ضرائب الضمان الاجتماعي والرعاية الطبية على وارن بافيت كثيراً. أولاً، لن يكون سقف الضمان الاجتماعي البالغ 97,500 دولار أمريكي ذا أهمية تُذكر بالنسبة له. ثانياً، تُطبق هذه الضرائب على الأجور، وليس على أرباح رأس المال، كما يُعرّف معظم دخله.
وهذا هو أفضل تخمين لدي بشأن الرياضيات وراء بيان السيد بوفيت.
تحديث: بعد نشر هذا المقال بفترة وجيزة، تلقيتُ الرد التالي. حرصًا على الإنصاف، أعرض الحجة التالية بأن السيد بافيت يدفع ضرائب باهظة.
قرأتُ باهتمام ردّك على الشخص "الغاضب" الذي يرى أنه من الظلم أن يدفع وارن بافيت نسبة ضرائب أقل من سكرتيرته. لقد خاب أملي في ردّك، الذي لا يُصحّح المعلومات الخاطئة التي تُشير إلى أن السيد بافيت يدفع ضرائب أقل من سكرتيرته.أولاً، كما أشرتَ، يُفرض على دخل الاستثمار ضريبة بنسبة 15%. وهذا يُمثل في الواقع ازدواجية ضريبية، إذ فُرضت على الدخل المكتسب الذي استثمره السيد بافيت ضريبة بنسبة 36%. بمقارنة التفاح بالبرتقال (دخل العمل مقابل دخل الاستثمار).
ثانيًا، لا ينبغي النظر إلى النسبة المئوية. في عالم المقامرة، ينبغي النظر إلى "العائد" بدلًا من ذلك. أنا متأكد تمامًا أن السيد بافيت دفع ملايين الدولارات ضرائب في العام نفسه الذي دفعت فيه سكرتيرته آلاف الدولارات.ألا ينبغي لقارئك أن يكون أكثر غضبًا لأن مواطنًا واحدًا في البلاد يدفع ضرائب تفوق بآلاف المرات ضرائب المواطنين الآخرين مقابل نفس الخدمات الحكومية؟ كان بإمكان أحدهم أن يقول بسهولة: "سمعت أن وارن بافيت دفع ضرائب تفوق سكرتيرته بمليون مرة، هذا أمرٌ مُشين!"
أردتُ فقط أن أُشير إلى أن النظر إلى "النسبة المئوية" فقط دون "العائد الفعلي" يُعدّ مغالطة. مثل العديد من مغالطاتك في المقامرة .
أطيب التحيات،
كيفن أ. (دالاس)
شكرًا لك على مجموعتك الممتعة من ألغاز الرياضيات. أنا وصديقتي ابتكرنا هذا الاختلاف في لغز القراصنة. ماذا لو كان جميع القراصنة متساوين في الرتبة، وفي كل جولة يُختار مُقترح القسمة بالقرعة؟ في هذا الاختلاف، افترض أن الأولوية القصوى لكل قرصان هي تعظيم المبلغ المتوقع من العملات التي سيستلمها. لديّ ما أعتقد أنه الحل، ولكن ربما ترغب في تجربته أولًا. شكرًا لك مجددًا.
أهلاً وسهلاً. إذا بقي قرصانان فقط، فلن يكون لدى القرصان المختار لتقديم الاقتراح أي أمل، لأن القرصان الآخر سيصوت بالرفض. سيحصل القرصان المسحوب على صفر، والآخر على ألف عملة. لذا، قبل السحب، القيمة المتوقعة مع بقاء قرصانين هي 500 عملة.
في مرحلة اختيار ثلاثة قراصنة، على القرصان المسحوب أن يقترح إعطاء أحد القراصنة الآخرين ٥٠١ و٤٩٩ لنفسه. سيصوت القرصان الذي يحصل على ٥٠١ بنعم، لأن قيمته أعلى من القيمة المتوقعة وهي ٥٠٠ عند التصويت بلا. قبل السحب، ومع بقاء ثلاثة قراصنة، لديك فرصة ١/٣ للحصول على ٠ أو ٤٩٩ أو ٥٠١ لكل منهم، بمتوسط ٣٣٣.٣٣.
في مرحلة القراصنة الأربعة، على القرصان المسحوب أن يختار إعطاء 334 لأي قرصين آخرين، و332 لنفسه. سيحصل بذلك على صوتين "نعم" من القراصنة الذين حصلوا على 334 عملة، لأنهم يفضلون الحصول على 334 على 333.33. بإضافة صوتك، ستحصل على 3 أصوات من أصل 4. قبل السحب، القيمة المتوقعة لكل قرصان هي متوسط 0، 334، 334، و332، أو 1000/4 = 250.
بنفس المنطق، في مرحلة الخمسة قراصنة، على القرصان المسحوب أن يختار إعطاء 251 لأي قرصانين، و498 لنفسه. على عكس المسألة الأصلية، ليس من الضروري العمل بطريقة عكسية. ما عليك سوى قسمة عدد العملات على عدد القراصنة، باستثناء عددك. ثم أعطِ نصف هذا المتوسط (مع التقريب للأسفل)، بالإضافة إلى عملة واحدة.
أحتاج إلى مساعدة في حل لغز "الخلود ٢". جائزة حل اللغز مليونا دولار أمريكي، وهو مبلغ ضخم بالنسبة لي. إليكم رابط لمقابلة، تتضمن صانع اللعبة نفسه، كريستوفر مونكتون (مستشار سابق لمارجريت تاتشر، من بين أمور أخرى). من الواضح أن اللعبة لا تتعلق بالمقامرة إطلاقًا، ولكن مع ذلك، ربما يمكنكم إضافة كلمة أو كلمتين عنها على صفحتكم الإلكترونية.
يتفاخر صانع اللعبة باستحالة حل اللغز، في الرابط المذكور أعلاه. بدأت أعتقد أنه محق، وأنه هو الوحيد الذي سيُثري في النهاية من بيع تلك اللعبة (السخيفة لكن الرائعة). كيف ستحل هذا النوع من الألغاز، وأنت عالم رياضيات؟
أتمنى أن تكون سعيدًا؛ لقد كنتُ مهووسًا بهذا اللغز منذ شهر تقريبًا. كنتُ محظوظًا (أو ربما غير محظوظ) بالعثور على اللغز المكون من ٢٥٦ قطعة في مكتبة بوردرز المحلية، لكنني اضطررتُ لشراء ألغاز الألغاز الأربعة من إيباي، من رجل في أستراليا.
كتبتُ برنامجًا يستطيع حل ألغاز القرائن الأربعة بسهولة. حلّ لغز القرائن الرابع المكون من 72 قطعة في أقل من ثانية. استخدمتُ برنامجًا بسيطًا يعتمد على أسلوب التكرار. رسمتُ مسارًا على اللوحة، بدءًا من الحدود. في كل موضع، كان البرنامج يمرّ على جميع القطع غير المستخدمة، باحثًا عن قطعة مناسبة. إذا وجدها، انتقل إلى المربع التالي، وإذا لم يجدها، تراجع مربعًا.
لقد ركّزتُ على حل لغز المليوني دولار المكون من 256 قطعة لأسابيع، ولم يُحقق أيٌّ منهما نجاحًا يُذكر. أميل إلى الموافقة على ما قاله مُنشئ الفيديو، وهو أنه حتى لو وُصِلَت عشرة ملايين من أسرع أجهزة الكمبيوتر في العالم، فقد لا يجدون الحل حتى مع زوال الكون. قد يظن المرء أنني كنتُ سأُصغي إلى تحذيره قبل البدء، ولكن أمام لغز جيد، فإن أي تفكير في الاستخدام العملي لوقتي يُصبح بلا جدوى.
لديّ الكثير من الأفكار للاختصارات، ولكن حتى لو سرّعت برنامجي بمليار مرة، فلن يُجدي ذلك نفعًا على الأرجح. سأكون مُعجبًا للغاية إذا حلّ أحدٌ هذا الأمر. ما يُقلقني حقًا هو شعوري بوجود فرعٍ غير مُكتشف من الرياضيات يُمكنه حلّ ألغاز كهذه بسهولة. إلى ذلك الحين، أعتقد أن التجربة والخطأ المُعمّق هو أفضل ما يُمكننا فعله لحلها. أجهزة الكمبيوتر اليوم بطيئةٌ جدًا، وعدد التركيبات هائلٌ جدًا، مما يُقلّل من فرص نجاح ذلك.

لنفترض أن المسافة بين مدينتين هي ١٠٠٠ ميل. في حالة انعدام الرياح، يمكن لطائرة أن تسافر بسرعة ٨٠٠ كيلومتر في الساعة. هل ستستغرق رحلة الذهاب والإياب وقتًا أطول في حالة انعدام الرياح، أم في حالة وجود رياح خلفية مباشرة بسرعة ١٠٠ كيلومتر في الساعة في اتجاه واحد، ورياح معاكسة مساوية لها في الاتجاه الآخر؟
في حالة انعدام الرياح، تستغرق الرحلة ساعتين في كل اتجاه، بإجمالي 4 ساعات. مع وجود رياح خلفية، ستحلق الطائرة بسرعة 600 ميل في الساعة، لتقطع الرحلة في 1000/600 = 1.667 ساعة. مع وجود رياح معاكسة، ستحلق الطائرة بسرعة 400 ميل في الساعة، لتقطع الرحلة في 1000/400 = 2.5 ساعة. لذا، في حالة وجود رياح، يبلغ إجمالي الوقت 4.167 ساعة، أي 10 دقائق إضافية.
هذا يُظهر خطورة حساب متوسط السرعات. لا يُمكن القول إن متوسط سرعة الرحلة هو 500 ميل في الساعة، إذا كانت 400 ميل في الساعة في اتجاه و600 ميل في الساعة في الاتجاه الآخر، لأن مسافة الـ 400 ميل في الساعة تمتد لفترة زمنية أطول.
إذا لم يكن هذا بديهيًا، فتخيل رياحًا سرعتها 800 كيلومتر في الساعة. ستستغرق الطائرة ساعة واحدة فقط مع الريح، لكنها ستبقى في مكانها في الاتجاه المعاكس، وستستغرق وقتًا طويلًا.
شاركتُ مؤخرًا في سحب على 7033 جائزة، ويُقال إن احتمال الفوز بها هو 1 من 13. اشتريتُ 5 تذاكر. ما هي احتمالاتي الفعلية للفوز؟ هناك أيضًا 40 جائزة كبيرة. ما هي احتمالاتي للفوز بجائزة كبيرة؟
لتبسيط الأمر، دعونا نتجاهل حقيقة أنه كلما زادت التذاكر التي تشتريها، انخفضت قيمة كل تذكرة لأنك تتنافس مع نفسك. مع ذلك، فإن احتمال خسارة جميع التذاكر الخمس هو (١٢/١٣) ٥ = ٦٧.٠٢٪. لذا، فإن احتمال الفوز بجائزة واحدة على الأقل هو ٣٢.٩٨٪. يوجد ٧٠٣٣ × ١٣ = ٩١٤٢٩ تذكرة إجمالية في الأسطوانة قبل شراء أي منها. ٩١٤٢٩ - ٤٠ = ٩١٣٨٩ ليست جوائز كبيرة. واحتمال عدم الفوز بأي جوائز كبيرة بخمس تذاكر هو (٩١٣٨٩ / ٩١٤٢٩) ٥ = ٩٩.٧٨٪. لذا، فإن احتمال الفوز بجائزة كبيرة واحدة على الأقل هو ٠.٢٢٪، أو ١ من ٤٥٨.
لديّ لغزٌ أحاول حله منذ بضعة أشهر، دون أي تقدم يُذكر. إن سمح الوقت، آمل أن تُساعدوني، فهو يُؤرقني طوال الليل :-). على أي حال، في مسرد مصطلحات "ما وراء العد - الملحق CAA" ، وردت ثلاث تسلسلات من الأرقام والحروف كمدخل في المسرد لـ"الأرقام السحرية". حتى أن أحد هذه الأرقام يظهر على غلاف الكتاب، لذا أفترض أنها ذات أهمية. هل لديكم أي أفكار؟
نادرًا ما أقول هذا، لكن ليس لديّ أدنى فكرة. كما ذكرتَ في رسالة إلكترونية أخرى، فإنهم يستخدمون صيغة الرقم التسلسلي للعملة الأمريكية، حرفين، بينهما رقم من عشرة أرقام. احترامًا لحقوق النشر، لن أذكر الأرقام هنا.
أرغب بمعرفة مصير تحدي لغز إترنيتي ٢. هل حُلّ؟ هل ما زلتم تعملون عليه؟
شكرًا لسؤالك. لا، لم أتطرق إلى هذه المشكلة منذ أن كتبتُ عنها في عمود "اسأل الساحر" بتاريخ ١٧ نوفمبر ٢٠٠٨. وفقًا لموقعهم الإلكتروني، سيكون لديهم "مواعيد تدقيق" في ٣١ ديسمبر ٢٠٠٩، و٢٠١٠ إذا لزم الأمر. في رأيي، لن تُحل المشكلة أبدًا.
التحديث: يبدو أن حجم ويب Eternity II لم يعد موجودًا.
قرأتُ بدهشة مدونة الساحر عن رسالة النقض التي أرسلها أرنولد شوارزنيجر. سؤالي يتعلق برد الحاكم السخيف والمتوقع. صرّح الحاكم بأنها مجرد "صدفة غريبة". على الرغم من الأدلة الظرفية القاطعة (كان راعي مشروع القانون ومُرسَل إليه الرسالة هو الشخص الذي شتم الحاكم قبل أسبوع)، هل لديك تقدير لاحتمالية كتابة حرف من سبعة أسطر بالضبط هذه العبارة بالصدفة؟ أعتقد أنه مع مراعاة الأحرف المستخدمة، سيكون الأمر أقل احتمالية من مجرد تحديد احتمال واحد من أصل ٢٦ لكل منها. لا يبدو أن حروف U وY، وخاصةً K، هي حروف شائعة لبدء الكلمات.
إذا كنت من السهل أن تغضب، يرجى الانتقال إلى السؤال التالي.
ولمصلحة القراء الذين لم يقرأوا هذه المدونة، أنظروا إلى الحرف الأول من كل سطر في هذه المذكرة التي كتبها حاكم ولاية كاليفورنيا أرنولد شوارزنيجر (PDF) ، بدءًا من السطر الذي يبدأ بالحرف F.
نوقش هذا في موقعي المرافق "ساحر فيغاس" . وللحصول على إجابة، وجدتُ تردد كل حرف من أول كلمة في اللغة الإنجليزية على ويكيبيديا .
تردد الكلمة حسب الحرف الأول
| خطاب | تكرار |
| أ | 11.60% |
| ب | 4.70% |
| ج | 3.51% |
| د | 2.67% |
| هـ | 2.00% |
| ف | 3.78% |
| ج | 1.95% |
| ح | 7.23% |
| أنا | 6.29% |
| ج | 0.63% |
| ك | 0.69% |
| ل | 2.71% |
| م | 4.37% |
| ن | 2.37% |
| ا | 6.26% |
| ص | 2.55% |
| س | 0.17% |
| ر | 1.65% |
| س | 7.76% |
| ت | 16.67% |
| يو | 1.49% |
| الخامس | 0.62% |
| و | 6.66% |
| إكس | 0.01% |
| ي | 1.62% |
| ز | 0.05% |
لتقدير احتمال أن تكون رسالة أرنولد مجرد مصادفة، ستكون Prob(F) × Prob(U) × ... × prob(U) = 0.0378 × 0.0149 × 0.0351 × 0.0069 × 0.0162 × 0.0626 × 0.0149 = 1 في 486,804,391,348. هذا لا يأخذ في الاعتبار حتى حقيقة أن فاصل السطر كان مكان المسافة بين الكلمتين.
وأود أن أشكر إليوت جيه وجوناثان ف. على مساهمتهما في هذا الحل.
عند سير الأمتعة في المطار، كلما زاد عدد الحقائب التي عليّ استلامها، طال انتظاري لخروجها جميعًا. إذا كانت معي حقيبة واحدة، فسأنتظر حتى خروج نصف الحقائب تقريبًا. إذا أخذت حقيبتين، فسيكون انتظاري أطول، وإذا كانت معي ثلاث حقائب، فسيكون الانتظار أطول. بافتراض أن حقائبي مُختلطة عشوائيًا مع الحقائب الأخرى، ما هي الصيغة العامة لعدد الحقائب التي سأنتظرها لخروج جميع حقائبي، من حيث عدد حقائبي وإجمالي عدد الحقائب؟
دعونا نحدد بعض المتغيرات أولاً، على النحو التالي:
n = عدد حقائبك
ب = العدد الإجمالي للأكياس
كلما زاد عدد الحقائب، اقتربت الإجابة من b×n/(n+1). بالنسبة لطائرة كبيرة، سيعطيك هذا تقديرًا جيدًا. مع ذلك، إذا كنت ترغب في الدقة، فالإجابة هي:
[b× combin (b,n)-(مجموع i=n إلى b-1 من combin(i,n))]/combin(b,n)
على سبيل المثال، إذا كان هناك 10 حقائب إجمالية، وأربعة منها تخصك، فإن وقت الانتظار المتوقع =
[10×كومبين(10,4)-كومبين(4,4)-كومبين(5,4)-كومبين(6,4)-كومبين(7,4)-كومبين(8,4)-كومبين(9,4)]/كومبين(10,4) = 8.8 أكياس.
حل:
عدد طرق اختيار n من b أكياس هو combin(b,n). لذا، فإن احتمالية اختيار جميع الأكياس من أول x أكياس هي combin(x,n)/combin(b,n). واحتمالية اختيار آخر كيس هو الكيس x الذي سيختاره هو (combin(x,n)-combin(x-1,n))/combin(b,n)، عندما تكون x>=n+1. وعندما تكون x=n، تكون 1/combin(b,n).
وبالتالي، فإن نسبة وقت الانتظار المتوقع إلى إجمالي وقت الانتظار هي:
n×combin(n,n)/combin(b,n) +
(ن+1)×(كومبين(ن+1,ن)-كومبين(ن,ن))/كومبين(ب,ن) +
(ن+2)×(كومبين(ن+2,ن)-كومبين(ن+1,ن))/كومبين(ب,ن) +
.
.
.
+
(ب-1)×(كومبين(ب-1,ن)-كومبين(ب-2,ن))/كومبين(ب,ن) +
ب×(combin(b,n)-combin(b-1,n))/combin(b,n)
من خلال أخذ مجموع تلسكوبي، يمكن تبسيط هذا إلى:
[ب×combin(b,n)-combin(b-1,n)-combin(b-2,n)-...-combin(n,n)]/combin(b,n)
كتب أحد القراء لاحقًا قائلًا إنه يمكن تبسيط الإجابة إلى n×(b+1)/(n+1). يمكن إثبات ذلك بالاستقراء، وهو أسلوب صحيح، ولكنه دائمًا ما يُشعرني بعدم الرضا العاطفي.
تم طرح هذا السؤال ومناقشته في منتدى موقعي المرافق Wizard of Vegas .
أبيع منحوتات. في المتوسط، من كل سبع عمليات بيع منحوتات، تكون واحدة منها سلحفاة، والباقي أنواع أخرى من المنحوتات. كم عدد السلاحف التي أحتاجها في المخزون لضمان عدم نفادها في عمليات البيع المئة القادمة؟

ليكن t هو عدد السلاحف المصنعة، و x هو عدد السلاحف المباعة.
pr(x<=t)=0.9
pr(x-14.29<=t-14.29)=0.9
العلاقات العامة((x-14.29)/3.5)<=(t-14.29)/3.5))=0.9
يتبع الجانب الأيسر من المتباينة توزيعًا طبيعيًا معياريًا (متوسط صفر، انحراف معياري واحد). تتطلب هذه الخطوة التالية دراسةً تمهيديةً للإحصاء، أو بعض الإيمان، لقبولها.
(t-14.29)/3.5 = normsinv(0.9) هذه هي دالة Excel.
(ت-14.29)/3.5 = 1.282
t-14.29 = 4.4870
ت = 18.77
من غير المرجح أن يشتري أحد 0.77 من تمثال سلحفاة، لذا أُقرّب إلى 19. وفقًا للتوزيع الثنائي، فإن احتمال بيع 18 أو أقل هو 88.35%، و19 أو أقل هو 92.74%. طُرح هذا السؤال ونوقش في منتدى موقعي المرافق "ساحر فيغاس" .
نجا خمسة بحارة من حادثة غرق سفينة. أول ما فعلوه هو جمع جوز الهند ووضعه في كومة كبيرة مشتركة. كانوا ينوون توزيعه بالتساوي لاحقًا، لكن بعد جهدهم المضني في جمع جوز الهند، شعروا بالتعب الشديد. لذلك ناموا ليلتهم، عازمين على توزيع الكومة في الصباح.
لكن البحارة لم يثقوا ببعضهم البعض. في منتصف الليل، استيقظ أحدهم ليأخذ حصته العادلة. قسّم الكومة إلى خمسة حصص متساوية، وتبقى ثمرة جوز هند واحدة. دفن حصته، وجمع الأكوام الأربعة الأخرى في كومة مشتركة جديدة، وأعطى جوز الهند المتبقي لقرد.
في الساعة 1:00 صباحًا، و2:00 صباحًا، و3:00 صباحًا، و4:00 صباحًا، يقوم كل من البحارة الأربعة الآخرين بنفس الشيء تمامًا.
في الصباح، لم يعترف أحدٌ بما فعله، واستمروا في خطتهم الأصلية بتقسيم الكومة بالتساوي. ومرة أخرى، تبقى ثمرة جوز هند واحدة، فأعطوها للقرد.
ما هو أصغر عدد ممكن من جوز الهند في الكومة الأصلية؟
"قم بالتمرير لأسفل 100 سطر للحصول على الإجابة.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
كان هناك ١٥,٦٢١ ثمرة جوز هند في الكومة الأصلية. انزل ١٠٠ سطر آخر للعثور على حلّ.
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
ليكن c هو عدد جوز الهند في الكومة الأصلية وليكن f هو الحصة النهائية لكل بحار بعد القسمة الأخيرة.
بعد أن يأخذ البحار 1 حصته ويعطي القرد جوز الهند الخاص به، سيكون هناك (4/5) × (ج - 1) = (4ج - 1) / 5 متبقيًا.
بعد أن يأخذ البحار 2 حصته ويعطي القرد جوز الهند الخاص به، سيكون هناك (4/5) × (((4c-1)/5)-1) = (16c-36)/25 متبقيًا.
بعد أن يأخذ البحار 3 حصته ويعطي القرد جوز الهند الخاص به، سيكون هناك (4/5) × (((16c-36)/25)-1) = (64c-244)/125 متبقيًا.
بعد أن يأخذ البحار الرابع حصته ويعطي القرد جوز الهند الخاص به، سيكون هناك (4/5) × (((64c-244)/125)-1) = (256c-1476)/625 متبقيًا.
بعد أن يأخذ البحار رقم 5 حصته ويعطي القرد جوز الهند الخاص به، سيكون هناك (4/5) × (((256c-1476) / 625) - 1) = (1024c-8404) / 3125 متبقيًا.
في الصباح سيكون نصيب كل بحار من الكومة المتبقية هو f = (1/5)×(((1024c-8404)/3125)-1) = (1024c-11529)/15625 متبقي.
إذن، السؤال هو: ما أصغر قيمة لـ c بحيث يكون f=(1024×c-11529)/15625 عددًا صحيحًا؟ لنعبر عن c بدلالة f.
(1024×ج-11529)/15625 = ف
1024 ج - 11529 = 15625×ف
1024 ج = 15625 ف + 11529
ج = (15625ف + 11529) / 1024
ج = 11+((15625×f+265)/1024)
ج = 11+15×f+(265×(f+1))/1024
إذن، ما أصغر قيمة لـ f بحيث يكون 265×(f+1)/1024 عددًا صحيحًا؟ ليس لـ 265 و1024 أي عوامل مشتركة، لذا فإن f+1 بمفردها ستكون قابلة للقسمة على 1024. أصغر قيمة ممكنة لـ f+1 هي 1024، لذا f=1023.
وبالتالي، ج = (15625×1023+11529)/1024 = 15,621.
وهذا هو عدد جوز الهند التي تلقاها كل شخص وكل قرد:
مشكلة جوز الهند
| بحار | جوز الهند |
| 1 | 4147 |
| 2 | 3522 |
| 3 | 3022 |
| 4 | 2622 |
| 5 | 2302 |
| قرد | 6 |
| المجموع | 15621 |
ديفيد فيلمر، الذي تحدَّاني بالسؤال، كان يعرف الإجابة مُسبقًا. في الواقع، سألني عن صيغة الحالة العامة لـ s بحارة، لكنني واجهتُ صعوبةً كافيةً في الحالة الخاصة لـ 5 بحارة. يُشير ديفيد إلى أن إجابة الحالة العامة هي c = s s+1 - s + 1.
سأترك هذا الدليل للقارئ.
وفيما يلي بعض الروابط للحلول البديلة للمشكلة:
قُدِّم لرجل ظرفان مليئان بالنقود. يحتوي أحد الظرفين على ضعف المبلغ الموجود في الظرف الآخر. بعد أن اختار الرجل ظرفته وفتحه وعدّه، أُتيحت له فرصة استبداله بالظرف الآخر. السؤال هو: هل هناك أي فائدة للرجل من استبدال الظرف؟
يبدو أنه بتبديل العملة، ستكون لدى الرجل فرصة ٥٠٪ لمضاعفة أمواله إذا كان الظرف الأول أقل قيمة، وفرصة ٥٠٪ لخفضها إلى النصف إذا كان الظرف الأول أعلى قيمة. لذا، لنفترض أن x هو المبلغ الموجود في الظرف الأول، وأن y هي قيمة تغييره:
ص = 0.5×(س/2) + 0.5×(2س) = 1.25س
لنفترض أن الظرف الأول كان يحتوي على ١٠٠ دولار. إذًا، هناك احتمال بنسبة ٥٠٪ أن يحتوي الظرف الآخر على ٢ × ١٠٠ دولار = ٢٠٠ دولار، واحتمال بنسبة ٥٠٪ أن يحتوي الظرف الآخر على (١/٢) × ١٠٠ دولار = ٥٠ دولارًا. في هذه الحالة، تكون قيمة الظرف:
0.5×(100 دولار/2) + 0.5×(2×100 دولار) = 125 دولارًا
هذا يعني أن الرجل سيزيد ثروته، في المتوسط، بنسبة ٢٥٪ بمجرد تغيير الظروف! كيف يمكن ذلك؟
يبدو هذا مفارقة رياضية، ولكنه في الحقيقة مجرد إساءة استخدام لمعادلة القيمة المتوقعة. كما ذكرتَ في السؤال، يبدو أن الظرف الآخر يجب أن يحتوي على قيمة أكبر بنسبة 25% من الظرف الذي اخترته. مع ذلك، إذا اخترتَ ذلك، فمن الأفضل اختيار الظرف الآخر من البداية. علاوة على ذلك، يمكنك استخدام هذه الحجة للتبديل بين الظرفين باستمرار إذا لم تتمكن من فتحهما قبل اتخاذ قرار التبديل. من الواضح أن هناك خللًا ما في حجة القيمة المتوقعة. السؤال هو: أين يكمن الخلل؟
لقد قضيتُ وقتًا طويلًا في قراءة هذه المسألة ومناقشتها على مر السنين. سمعتُ وقرأتُ العديد من الشروحات حول خطأ حجة ص = ٠٫٥س + ٠٫٥ × ٢س = ١٫٢٥س. استخدم الكثيرون صفحاتٍ طويلةً من الرياضيات المتقدمة في الشرح، وهو ما لا أعتقد أنه ضروري. إنه سؤال بسيط يتطلب إجابةً بسيطة. لذا، هذه هي محاولتي.
يجب أن تكون حذرًا جدًا فيما تفعله مع حقيقة أن أحد الظرفين يحتوي على ضعف المبلغ الموجود في الآخر. لنسمِّ المبلغ في الظرف الأصغر S، والأكبر L. إذن لدينا:
ل=2×س
S=0.5×L
لاحظ كيف يُطبّق العاملان 2 و0.5 على مظروفين مختلفين . لا يمكنك استخدام كلا العاملين وتطبيقهما على نفس المبلغ. إذا كان المظروف الأول يحتوي على 100 دولار، فإذا كان المظروف الأصغر، فسيكون المظروف الآخر 200 دولار. إذا كان المظروف الأكبر يحتوي على 100 دولار، فسيكون المظروف الآخر 50 دولارًا. وبالتالي، سيكون المظروف الآخر 50 دولارًا أو 200 دولار. ومع ذلك، لا يمكنك الجزم بأن هناك احتمالًا 50/50 لكل منهما. هذا لأن ذلك يعني تطبيق العاملين 0.5 و2 على نفس المبلغ، وهو أمر غير ممكن. بدون معرفة توزيع الجوائز في البداية، لا يمكنك تحديد مبالغ محتملة للمظروف الثاني.
إذا كانت معادلة 0.5x/2x خاطئة، فما هي الطريقة الصحيحة لحساب القيمة المتوقعة للظرف الآخر؟ سأقول إن الفرق بين الظرفين هو LS = 2S-S = S. بالتبديل، ستربح أو تخسر S، أيًا كان. إذا كان الظرفان يحتويان على 50 دولارًا و100 دولارًا، فإن التبديل سيربح أو يخسر 50 دولارًا. إذا كان الظرفان يحتويان على 100 دولار و200 دولار، فإن التبديل سيربح أو يخسر 100 دولار. في كلتا الحالتين، الربح المتوقع بالتبديل هو 0. أعتقد أنه يمكنني القول إنه إذا كان الظرف الأول يحتوي على 100 دولار، فهناك احتمال بنسبة 50% أن يكون الفرق في الظرف الآخر 50 دولارًا، واحتمال بنسبة 50% أن يكون 100 دولار. لذا، فإن الفرق المتوقع هو 75 دولارًا. وبالتالي، فإن القيمة المتوقعة للظرف الآخر هي 0.5×(100 دولار + 75 دولار) + 0.5×(100 دولار - 75 دولار) = 0.5×(175 دولار + 25 دولار) = 100 دولار.
آمل أن يكون هذا مفهومًا. هذه المشكلة دائمًا ما تثير الكثير من التعليقات. إذا كانت لديكم أي تعليقات، فلا تراسلوني مباشرةً، بل انشروها في منتدى Wizard of Vegas. الرابط أدناه.
تم طرح هذا السؤال ومناقشته في منتدى موقعي المرافق Wizard of Vegas .
الروابط
لنفترض وجود مبارزة ثلاثية (ترويل) بين المشاركين أ، ب، ج. يتقاتلون حتى الموت من أجل امرأة. جميعهم رجال، ويتفقون جميعًا على القواعد التالية.
- يشكل المشاركون الثلاثة مثلثًا.
- كل واحد منهم لديه رصاصة واحدة فقط.
- أ يبدأ أولا، ثم ب، ثم ج.
- احتمالية إصابة الهدف المقصود هي 10%.
- احتمالية إصابة B للهدف المقصود هي 60%.
- احتمالية إصابة C للهدف المقصود هي 90%.
- لا يوجد إطلاق نار عرضي.
- إطلاق النار في الهواء (عمدا) وإطلاق النار على نفسك مسموح به، وهما دائما ناجحان.
- إذا بقي اثنان أو ثلاثة ناجين بعد أي جولة، يُعطى كلٌّ منهم رصاصة جديدة. ثم يتناوبون على إطلاق النار، بنفس الترتيب، متجاوزين أي شخص مات سابقًا.
- كل المشاركين الثلاثة هم منطقيون مثاليون.
من يجب أن يستهدفه أ في البداية؟ ما احتمال نجاته من كل هدف أولي؟
نُوقش هذا اللغز في برنامج "مثير للاهتمام للغاية" على قناة بي بي سي. مرر لأسفل ١٠٠ سطر للعثور على الإجابة والحل.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
إليكم احتمالات فوز اللاعب (أ) وفقًا لكل هدف أولي. كما ترون، يتعاظم احتمال فوز اللاعب (أ) بإطلاق النار في الهواء عمدًا.
احتمالات ترويل
| الاستراتيجية | احتمال الفوز |
| هواء | 13.887% |
| أ | 0.000% |
| ب | 12.560% |
| ج | 13.094% |
للحل، لنستخدم الرمز Pr(X) للدلالة على احتمال بقاء المجموعة X فقط بعد الجولة. ولنستخدم المصطلح Pr(X*) للدلالة على احتمال فوز المجموعة X بالجولة في النهاية، بعد تكرار اللعبة حتى تتغير حالة اللعبة بإصابة أحد اللاعبين. لنفترض أن Pr(X**) هو احتمال أن يكون اللاعب X هو الناجي الوحيد. لإيجاد الاحتمالات النهائية، لننظر أولًا إلى حالتي اللاعبين. من الواضح أن كلًا منهما سيُصيب الآخر.
أ مقابل ب
- Pr(A) = 0.1
- Pr(B) = 0.9×0.6 = 0.54
- Pr(AB) = 0.9×0.4 = 0.36
إذا نجا كلاهما، فسيتكرر الأمر حتى يبقى ناجٍ واحد فقط. لذا، تكون احتمالات أن يكون الناجي الأخير هي:
- العلاقات العامة(A*) = العلاقات العامة(A)/(1- العلاقات العامة(AB)) = 0.1/0.64 = 0.15625
- العلاقات العامة(B*) = العلاقات العامة(B)/(1- العلاقات العامة(AB)) = 0.54/0.64 = 0.84375
أ مقابل ج
- Pr(A) = 0.1
- Pr(C) = 0.9×0.9 = 0.81
- Pr(AC) = 0.9×0.1 = 0.09
إذا نجا كلاهما، فسيتكرر الأمر حتى يبقى ناجٍ واحد فقط. لذا، تكون احتمالات أن يكون الناجي الأخير هي:
- العلاقات العامة(A*) = العلاقات العامة(A)/(1- العلاقات العامة(AC)) = 0.1/0.91 = 0.10989011
- العلاقات العامة(C*) = العلاقات العامة(B)/(1- العلاقات العامة(AC)) = 0.81/0.91= 0.89010989
ب مقابل ج
- Pr(B) = 0.6
- Pr(C) = 0.4×0.9 = 0.36
- Pr(BC) = 0.$×0.1 = 0.04
إذا نجا كلاهما، فسيتكرر الأمر حتى يبقى ناجٍ واحد فقط. لذا، تكون احتمالات أن يكون الناجي الأخير هي:
- العلاقات العامة(B*) = العلاقات العامة(A)/(1- العلاقات العامة(BC)) = 0.6/.96 = 0.625
- العلاقات العامة(C*) = العلاقات العامة(B)/(1- العلاقات العامة(BC)) = 0.36/.96= 0.375
الآن، نحن مستعدون لتحليل حالة اللاعبين الثلاثة. لننظر إلى الحالة التي يستهدف فيها اللاعب (أ) اللاعب (ب).
ثلاثة لاعبين - أ يهدف إلى ب
إذا أصابت الكرة أ الكرة ب، فإن الكرة ج ستنجو حتمًا، وقد تصيب الكرة أ أو لا تصيبها. لذا، فإن نتيجتين محتملتين لإصابة الكرة ب هما AC وC. إذا أخطأت الكرة أ الكرة ب، فإن الكرة ب ستستهدف الخطر الأكبر ج. إذا أصابت الكرة ب الكرة ج، فإن الكرة أ و B ستنجو. إذا أخطأت الكرة ب الكرة ج، فإن الكرة ج ستستهدف الخطر الأكبر ب. إذا أخطأت الكرة ج الكرة ب، فإن الكرة الثلاثة ستنجو. إذا أصابت الكرة ج الكرة ب، فإن الكرة أ و C ستنجو. لذا، فإن النتائج المحتملة هي C، AB، AC، وABC.
- Pr(A) = 0.
- Pr(B) = 0.
- Pr(C) = 0.1 × 0.9 = 0.09. يتحقق ذلك بضرب A لـ B، ثم ضرب C لـ A.
- Pr(AB) = 0.9 × 0.6 = 0.54. يتحقق ذلك بفشل A في الوصول إلى B، ثم اصطدام B بـ C.
- Pr(AC) = 0.1 × 0.1 + 0.9 × 0.4 × 0.9 = 0.334. يمكن تحقيق ذلك بطريقتين. الأولى: أن يصطدم A بـ B، ثم يفوت C A. الثانية: أن يفوت A B، ثم يفوت B C، ثم يصطدم C بـ B.
- Pr(BC) = 0.
- Pr(ABC) = 0.9 × 0.4 × 0.1 = 0.036. يتحقق ذلك من خلال فقدان جميع القيم الثلاث.
وبنفس المنطق الذي اتبعناه في حالات اللاعبين، يمكننا قسمة كل نتيجة على (1-Pr(ABC))=0.964 لإيجاد احتمالات كل حالة، على افتراض أن حالة اللعبة تغيرت بعد الجولة.
- العلاقات العامة(C*) = 0.09/0.964 = 0.093361.
- العلاقات العامة (AB*) = 0.54/0.964 = 0.560166.
- العلاقات العامة (AC *) = 0.334 / 0.964 = 0.346473.
من خلال اللعب بين لاعبين، نعلم أنه إذا انتهى الأمر بفوز أ و ب، فسيفوز أ باحتمال 0.15625، وب باحتمال 0.84375. وإذا انتهى الأمر بفوز أ و ج، فسيفوز أ باحتمال 0.109890، وج باحتمال 0.890110.
- Pr(A**) = (0.560165975 × 0.15625) + (0.346473029 × 0.10989011) = 0.125600. يمكن أن يكون A هو الفائز بطريقتين: (1) الوصول إلى حالة AB، ثم الفوز، أو (2) الوصول إلى حالة AC ثم الفوز.
- Pr(B**) = 0.560166 × 0.84375 = 0.472640. سيكون B هو الفائز إذا وصل إلى حالة AB، وعندها يفوز B.
- Pr(C**) = 0.093361 + (0.346473 × 0.890110) = 0.401760. يمكن لـ C الفوز بفوز A على B، ثم فوز C على A في الجولة الأولى، أو بوصوله إلى حالة AC، ثم فوز C.
لذا، إذا كانت استراتيجية أ هي استهداف ب في البداية، فإن احتمال كونه الناجي الوحيد هو 12.56%.
ثلاثة لاعبين - أ يهدف إلى ج
إذا أصابت الكرة أ الكرة ج، فإن الكرة ب ستنجو حتمًا، وقد تصيب الكرة أ أو لا تصيبها. لذا، فإن نتيجتين محتملتين لإصابة الكرة ج هما: أ ب و ب. إذا أخطأت الكرة أ ج، فإن الكرة ب ستستهدف الخطر الأكبر ج. إذا أصابت الكرة ب ج، فإن الكرة أ و ب ستنجو. إذا أخطأت الكرة ب ج، فإن الكرة ج ستستهدف الخطر الأكبر ب. إذا أخطأت الكرة ج ب، فإن الكرة الثلاثة ستنجو. إذا أصابت الكرة ج ب، فإن الكرة أ و ج ستنجو. لذا، فإن النتائج المحتملة هي: ب، أ ب، أ ج، أ ب ج، أ ب ج.
- Pr(A) = 0.
- Pr(B) = 0.1 × 0.6 = 0.06.
- Pr(C) = 0.
- Pr(AB) = (0.1 × 0.4) + (0.9 × 0.6) = 0.04+0.54 = 0.58. يمكن تحقيق ذلك بطريقتين.الأول هو أن يضرب أ ج، ثم يخطئ ب أ. الثاني هو أن يخطئ أ ب، ثم يخطئ ب ج.
- Pr(AC) = 0.9 × 0.4 × 0.9 = 0.324. يتحقق ذلك بأن A يفتقد C، وB يفتقد C، وC يصطدم بـ B.
- Pr(BC) = 0.
- Pr(ABC) = 0.9 × 0.4 × 0.1 = 0.036. يتحقق ذلك من خلال فقدان جميع القيم الثلاث.
وبنفس المنطق الذي اتبعناه في حالات اللاعبين، يمكننا قسمة كل نتيجة على (1-Pr(ABC))=0.964 لإيجاد احتمالات كل حالة، على افتراض أن حالة اللعبة تغيرت بعد الجولة.
- العلاقات العامة (ب*) = 0.06/0.964 = 0.062241.
- العلاقات العامة (AB*) = 0.58/0.964 = 0.601660.
- العلاقات العامة (AC *) = 0.324 / 0.964 = 0.336100.
بنفس منطق الحل لحالة A يهدف إلى B:
- العلاقات العامة(A**) = (0.601660 × 0.15625) + (0.336100 × 0.10989011) = 0.130943.
- العلاقات العامة (ب**) = 0.062241 + 0.601660 × 0.84375 = 0.569891.
- العلاقات العامة(C**) = 0.336100 × 0.890110 = 0.299166.
لذا، إذا كانت استراتيجية أ هي استهداف ج في البداية، فإن احتمال كونه الناجي الوحيد هو 13.09%.
ثلاثة لاعبين - أخطأ عمدًا
بعد أن يُخطئ أ عمدًا، سيُصوِّب ب على التهديد الأكبر ج. إذا أصاب ب ج، فسينجو أ و ب. إذا أخطأ ب ج، فسيُصوِّب ج على التهديد الأكبر ب. إذا أخطأ ج ب، فسينجو الثلاثة جميعًا. إذا أصاب ج ب، فسينجو أ و ج. إذن، النتائج المحتملة هي أ ب، أ ج، أ ب ج.
- Pr(A) = 0.
- Pr(B) = 0.
- Pr(C) = 0.
- Pr(AB) = 0.6. يتحقق ذلك باصطدام B بـ C.
- Pr(AC) = 0.4 × 0.9 = 0.36. يتحقق ذلك بفقدان B لـ C، ثم اصطدام C بـ B.
- Pr(BC) = 0.
- Pr(ABC) = 0.4 × 0.1 = 0.04. يتحقق ذلك من خلال فقدان جميع القيم الثلاث.
وبنفس المنطق الذي اتبعناه في حالات اللاعبين، يمكننا قسمة كل نتيجة على (1-Pr(ABC))=0.96 لإيجاد احتمالات كل حالة، على افتراض أن حالة اللعبة تغيرت بعد الجولة.
- Pr(AB*) = 0.6/0.96 = 0.625.
- Pr(AC*) = 0.36/0.96 = 0.375.
بنفس منطق الحل لحالة A يهدف إلى B:
- العلاقات العامة(A**) = (0.625 × 0.15625) + (0.375 × 0.109890) = 0.138865.
- العلاقات العامة (ب**) = 0.625 × 0.84375 = 0.527344.
- العلاقات العامة(C**) = 0.375 × 0.890110 = 0.333791.
لذا، إذا كانت استراتيجية أ هي استهداف ج في البداية، فإن احتمال كونه الناجي الوحيد هو 13.89%.
تم طرح هذا السؤال ومناقشته في منتدى موقعي المرافق Wizard of Vegas .
عند مقارنة عنصرين في وقت واحد، ما هي أسرع طريقة لفرز القائمة، مع تقليل الحد الأقصى لعدد المقارنات؟
هناك عدة طرق بنفس الجودة تقريبًا. مع ذلك، أجد أن أسهلها فهمًا هي فرز الدمج . إليك كيفية عملها:
- قسّم القائمة إلى قسمين. استمر في تقسيم كل مجموعة فرعية إلى قسمين، حتى يصبح حجم كل مجموعة فرعية ١ أو ٢.
- قم بفرز كل مجموعة فرعية من 2 عن طريق وضع العضو الأصغر أولاً.
- دمج أزواج المجموعات الجزئية معًا. كرّر العملية حتى تحصل على قائمة واحدة مرتبة فقط.
طريقة دمج قائمتين هي مقارنة العنصر الأول في كل قائمة، ووضع العنصر الأصغر في قائمة جديدة. ثم كرر العملية، وضع العنصر الأصغر بعد العنصر الأصغر من المقارنة السابقة. استمر في التكرار حتى يتم دمج المجموعتين في مجموعة واحدة مرتبة. إذا كانت إحدى القائمتين الأصليتين فارغة، يمكنك إضافة القائمة الأخرى إلى نهاية القائمة المدمجة.
يوضح الجدول التالي الحد الأقصى لعدد المقارنات اللازمة وفقًا لعدد العناصر الموجودة في القائمة.
دمج الفرز
| عناصر | الحد الأقصى للمقارنات |
| 1 | 0 |
| 2 | 1 |
| 4 | 5 |
| 8 | 17 |
| 16 | 49 |
| 32 | 129 |
| 64 | 321 |
| 128 | 769 |
| 256 | 1,793 |
| 512 | 4,097 |
| 1,024 | 9,217 |
| 2,048 | 20,481 |
| 4,096 | 45,057 |
| 8,192 | 98,305 |
| 16,384 | 212,993 |
| 32,768 | 458,753 |
| 65,536 | 983,041 |
| 131,072 | 2,097,153 |
| 262,144 | 4,456,449 |
| 524,288 | 9,437,185 |
| 1,048,576 | 19,922,945 |
| 2,097,152 | 41,943,041 |
تم طرح هذا السؤال ومناقشته في منتدى موقعي المرافق Wizard of Vegas .
في 29 أكتوبر/تشرين الأول 2010، نشرت صحيفة "لاس فيغاس ريفيو جورنال" استطلاع رأي حول سباق ريد-أنغل لمجلس الشيوخ. وذكرت الصحيفة أنه في استطلاع شمل 625 ناخبًا محتملًا، فاز أنغل بنسبة 49%، بينما فاز ريد بنسبة 45%. وأشارت أيضًا إلى أن هامش الخطأ بلغ 4%. إليكم أسئلتي:
- ما هي احتمالية فوز أنجل؟
- ما هي نسبة الثقة 95% لحصة أنجل من الأصوات؟
- ماذا يعني هامش الخطأ؟
أعتذر عن الرد المتأخر. كتبتُ ما يلي قبل الانتخابات.
أولاً، سأتخلص من نسبة الـ 6% المتبقية، وهم إما مترددون أو سيبددون أصواتهم على مرشح من حزب ثالث أو "لا شيء مما سبق"، وهو خيار وارد في نيفادا. قد يختلف البعض مع هذا الافتراض. بصراحة، هناك سبب آخر لتجاهلهم وهو أن الحسابات تصبح أكثر تعقيدًا مع وجود أكثر من مرشحين. لذا، بعد التقريب، نحصل على 306 أصوات لأنجل، و281 صوتًا لريد، ليصبح المجموع 587 صوتًا في العينة.
سأستخدم التقريب المعياري للإجابة على هذا السؤال. لو كنتُ من مُحبي الكمال، لاستخدمتُ توزيع T ، لأن المتوسط والتباين الفعليين غير معروفين. مع ذلك، في رأيي، حجم عينة ٥٨٧ مناسب تمامًا للتوزيع الطبيعي.
حجم العينة = 306+281 = 587.
متوسط عينة الزاوية هو 306/587 = 0.521295.
الانحراف المعياري المقدر للمتوسط هو (0.521295 × 0.478705 / (587-1))^0.5 = 0.0206361.
حصة الزاوية فوق 50% هي (0.521295-0.5)/0.0206361 = 1.031917 انحراف معياري.
وفقًا للتوزيع الطبيعي، فإن احتمال فوز ريد بفارق 1.031917 انحرافًا معياريًا أعلى من التوقعات هو 0.151055. يمكن حساب ذلك في برنامج إكسل باستخدام الدالة NORMSDIST(-1.031917). لذا، فإن احتمال فوز أنجل هو 1-0.151268 = 84.89%.
لإنشاء فاصل ثقة 95%، يُرجى ملاحظة أن نقطة 2.5% على جانبي المنحنى الغاوسي تقع عند 1.959964 انحرافًا معياريًا عن المتوسط. يُمكن إيجاد ذلك في برنامج إكسل باستخدام الدالة NORMSINV(0.975). كما ذُكر سابقًا، الانحراف المعياري المُقدّر لمتوسط العينة هو 0.0206361. لذا، هناك احتمال بنسبة 95% أن يحصل أيٌّ من المرشحين على نتيجة استطلاع رأي ضمن 0.0206361 × 1.959964 = 0.040446 انحرافًا معياريًا. لذا، فاصل ثقة أنجل بنسبة 95% هو 0.521295 +/- 0.040446 = 48.08% إلى 56.17%.
قيل لي إنه من غير الصحيح رياضيًا صياغة ذلك على النحو التالي: "نسبة أنجل من جميع أصوات أنجل/ريد لديها احتمال 95% أن تقع بين 48.08% و56.17%". هكذا صغتُ إجابتي في البداية، لكن إحصائيَّين اشمئزا من صياغتي. ولإعادة صياغة ردهما، قالا إنه عليّ استخدام صيغة المبني للمجهول، والقول إن "48.08% و56.17% ستحيطان بنسبة 95% لحصة أنجل". بصراحة، يبدو الأمر نفسه بالنسبة لي. مع ذلك، أكدا أن فترة الثقة عشوائية وحصة أنجل ثابتة، وأن صياغتي الأصلية كانت توحي بالعكس. على أي حال، آمل أن يرضى الإحصائيون التكراريون بالصياغة الثانية.
هامش الخطأ هو نصف الفرق بين طرفي فاصل الثقة 95%. في هذه الحالة (56.17% - 48.08%)/2 = 4.04%.
ومتابعة لذلك، إليكم النتائج الفعلية:
ريد: 361,655
الزاوية: 320,996
أخرى: 21,979
إذن، باستثناء الأصوات "الأخرى"، حصل ريد على 53.0% وأنجل على 47.0%. وهذا فوز مريح بنسبة 6% لريد. وهذا يطرح سؤالاً: لماذا كان الاستطلاع خاطئاً إلى هذا الحد؟ هل كان ذلك محض صدفة؟ هل غيّر الناخبون آراءهم؟ أم كان استطلاعاً سيئاً من البداية؟ أترك هذه الأسئلة للقارئ (أكره أن تذكر الكتب المدرسية ذلك).
تم طرح هذا السؤال ومناقشته في منتدى موقعي المرافق Wizard of Vegas .
لقد جربتُ حاسبتك الاكتوارية. لماذا احتمال وصولي إلى عمري المتوقع عند الوفاة أقل من ٥٠٪؟
أنت تخلط بين المتوسط الحسابي والوسيط. لنأخذ حالتي كمثال. أنا رجل أبلغ من العمر 45 عامًا. متوسط عمري المتوقع هو 78.11 عامًا، ومع ذلك، لديّ فرصة 50.04% للوصول إلى سن الثمانين.
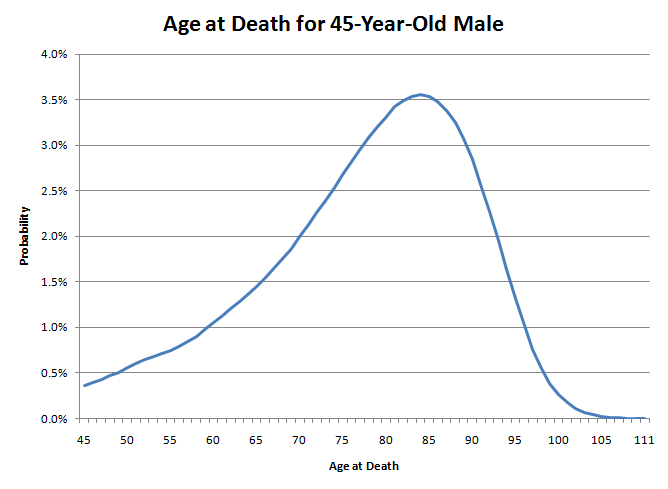
سيكون عمري عند الوفاة أشبه برمي سهم على هذا الرسم البياني. لاحظ كيف أن الذيل الأيسر أعرض بكثير من الأيمن. هذا يعني أن احتمال وفاتي الآن منخفض جدًا. ومع ذلك، مع تقدمي في العمر، سيستمر احتمال الوفاة في العام المقبل في الارتفاع. على سبيل المثال، بالنسبة لرجل يبلغ من العمر 45 عامًا، فإن احتمال البقاء على قيد الحياة حتى سن 46 مرتفع جدًا بنسبة 99.64%. ومع ذلك، في سن 85، فإن احتمالية الوصول إلى سن 86 هي 89.21% فقط. الأمر أشبه بغرز الطبيعة سكينًا في ظهرك ببطء. في البداية قد لا تقتلك، ولكن مع مرور كل عام، تزداد احتمالية ذلك تدريجيًا. ومع ذلك، بمجرد أن تصل إلى أواخر السبعينيات، تقول الطبيعة كفى من الألعاب وتبدأ في إغراقك بها.
إذا راهن عدد كبير من الرجال البالغين من العمر 45 عامًا على هذا الرسم البياني، فإن 49.96% منهم سيُصيبون بين 45 و79 عامًا، و50.04% سيصيبون بين 80 و111 عامًا. مع ذلك، فإن النصف المحظوظ الذي يصل إلى يمين الرسم البياني لن يعيش على الأرجح أكثر من 80 عامًا. بمجرد أن يصل الرجل إلى 80 عامًا، يتوقع أن يعيش 7.78 عامًا إضافية فقط. في الوقت نفسه، سيموت الكثير من النصف غير المحظوظ الذي لا يصل إلى 80 عامًا في سن أصغر بكثير. لذا، فإن الوفيات الكثيرة في سن الشباب هي التي تُخفض متوسط العمر المتوقع.
في موقف مماثل، ضع في اعتبارك حجر نرد مرقم 10، 20، 30، 31، 32، 33. المتوسط هو 26، ولكن هناك فرصة 2/3 للحصول على رقم أكبر من ذلك.
كمثال على اختلاف المتوسط الحسابي والوسيط، لنفترض أننا أضفنا حالتي وفاة إلى العينة. إحداهما في سن 46 والأخرى في سن 81. لن يتغير احتمال الوصول إلى سن 80، لكن متوسط العمر المتوقع عند سن 45 سينخفض.
تم طرح هذا السؤال ومناقشته في منتدى موقعي المرافق Wizard of Vegas .
تخيل شريطًا مطاطيًا شديد المرونة، طوله كيلومتر واحد دون شد. يتمدد بمعدل كيلومتر واحد في الثانية. بعد ذلك، تخيل نملة عند أحد طرفي الشريط المطاطي. في اللحظة التي يبدأ فيها الشريط بالتمدد، تزحف النملة نحو الطرف الآخر بسرعة، بالنسبة لموقعها الحالي، تبلغ سنتيمترًا واحدًا في الثانية. هل ستصل النملة إلى الطرف الآخر؟ إذا كان الأمر كذلك، فمتى؟
نعم، سيحدث ذلك بعد ١٠٠,٠٠٠ -١ ثانية. راجع موقعي mathproblems.info ، المسألة ٢٠٦، لحلين.
تم طرح هذا السؤال ومناقشته في منتدى موقعي المرافق Wizard of Vegas .
هل تعتقد أن كفاءة استهلاك الوقود الأفضل تستحق التكلفة الإضافية لسيارة هجينة؟ كم كيلومترًا يجب أن تقطعها لتحقيق التعادل؟
سؤال جيد. للإجابة عليه، فكرتُ في شراء سيارة تويوتا هايلاندر. سعر التجزئة للطراز الهجين القياسي هو 37,490 دولارًا أمريكيًا. أما بالنسبة لنفس السيارة ذات الدفع الرباعي غير الهجينة، فيبلغ سعرها 29,995 دولارًا أمريكيًا. لذا، يضيف المحرك الهجين 7,495 دولارًا أمريكيًا إلى سعرها.
يبلغ معدل استهلاك الوقود للسيارة الهجينة ٢٨ ميلاً في الساعة، داخل المدينة وعلى الطريق السريع. بينما يبلغ معدل استهلاك السيارة غير الهجينة ١٧ ميلاً في الساعة داخل المدينة و٢٢ ميلاً على الطريق السريع. لنأخذ المتوسط ١٩.٥ ميلاً.
الصيغة العامة لعدد الأميال اللازمة لتحقيق التعادل هي h×m h ×m r /(g×(m h -m r ))، حيث
ح = التكلفة الإضافية للهجين.
g = تكلفة جالون من الغاز.
م ر = المسافة المقطوعة بالسيارة غير الهجينة (الحرف "r" يشير إلى السيارة العادية).
م س = المسافة المقطوعة بالسيارة الهجينة.
يستخدم الجدول التالي هذه الصيغة للعثور على نقطة التعادل لأسعار مختلفة للغاز من 2 إلى 5 دولارات للغالون.
نقطة التعادل الهجينة
| تكلفة الغاز | عدد الأميال |
| 2.00 دولار | 240,722 |
| 2.25 دولارًا | 213,975 |
| 2.50 دولارًا | 192,577 |
| 2.75 دولارًا | 175,070 |
| 3.00 دولار | 160,481 |
| 3.25 دولارًا | 148,136 |
| 3.50 دولارًا | 137,555 |
| 3.75 دولارًا | 128,385 |
| 4.00 دولار | 120,361 | 4.25 دولارًا | 113,281 |
| 4.50 دولارًا | 106,987 |
| 4.75 دولارًا | 101,357 |
| 5.00 دولارًا | 96,289 |
لذا، بسعر 3 دولارات للغالون الحالي هنا في لاس فيغاس، ستحتاج إلى قطع أكثر من 160,481 ميلاً بالسيارة لتحقيق أفضلية. هذا لا يشمل النفقات الأخرى التي قد تصاحب السيارات الهجينة، مثل تكلفة استبدال البطاريات الباهظة، ولا أي نقاط بيئية متوقعة لاستهلاك أقل للوقود الأحفوري.
تم طرح هذا السؤال ومناقشته في منتدى موقعي المرافق Wizard of Vegas .
ما هي نسبة الجينات المشتركة بيني وبين الأخ أو الأخت الكاملين، باستثناء التوأم المتطابق؟
1/2.
إذا استخدمنا لعبة الكينو للمقارنة، فسيكون لدى كل شخص 40 جينًا، كل منها مُمَثَّل بكرة كينو. ومع ذلك، سيكون لكل كرة رقم فريد. عندما يتزاوج شخصان غير مرتبطين، يكون الأمر أشبه بدمج 80 كرة بينهما في وعاء، واختيار 40 جينًا عشوائيًا لنسل التزاوج.
عندما خُلقت، حصلت على نصف الكرات في القادوس، وضاع النصف الآخر. عندما خُلقت، حصل أخوك أو أختك على نصف الكرات المسحوبة عند ولادتك، والنصف الآخر غير المسحوب. لذا، فأنتما متطابقان وراثيًا بنسبة ٥٠٪. وللسبب نفسه، إذا سُحبت ٤٠ رقمًا في لعبة الكينو، فإن سحبتين متتاليتين سينتج عنهما ٢٠ كرة مشتركة في المتوسط.
تم طرح هذا السؤال ومناقشته في منتدى موقعي المرافق Wizard of Vegas .
مصنعٌ يُنتج طاولاتٍ وكراسي مُجهّزٌ بعشرة مناشير، وستة مخارط، وثمانية عشر آلة صنفرة. يستغرق تصنيع كرسيٍّ واحدٍ عشر دقائق على المنشار، وخمس دقائق على المخرطة، وخمس دقائق من الصنفرة. أما تصنيع طاولةٍ واحدةٍ فيستغرق خمس دقائق على المنشار، وخمس دقائق على المخرطة، وعشرون دقيقة من الصنفرة. يُباع الكرسي بعشرة دولارات، بينما تُباع الطاولة بعشرين دولارًا. كم عدد الطاولات والكراسي التي يجب أن يُنتجها المصنع في الساعة لتحقيق أعلى إيرادات، وما هي هذه الإيرادات؟
لنفترض أن c يمثل عدد الكراسي المُصنّعة في الساعة، وt يمثل عدد الطاولات. ستكون إيرادات الساعة 10×c + 20×t.
تنتج المناشير العشرة 600 دقيقة من النشر في الساعة. علمنا أن الكرسي يستغرق 10 دقائق من النشر، والطاولة 5 دقائق. لذا، يحد هذا من إنتاج الساعة إلى:
(1) 10c + 5t <= 600
تنتج المخرطات الستة 360 دقيقة من الخراطة في الساعة. علمنا أن الكرسي يستغرق 5 دقائق من المنشار، والطاولة 5 دقائق. لذا، يحد هذا من إنتاج الساعة إلى:
(2) 5ج + 5ت <= 360
تنتج آلات الصنفرة الثمانية عشر 1080 دقيقة صنفرة في الساعة. علمنا أن الكرسي يستغرق 5 دقائق من وقت المنشار، والطاولة 20 دقيقة. لذا، يحد هذا من إنتاج الساعة إلى:
(3) 5 ج + 20 ت <= 1080
يوضح الرسم البياني التالي القيود الثلاثة التي تفرضها مجموعات الآلات الثلاثة. يمكن للمصنع إنتاج أي مجموعة من الكراسي والطاولات ضمن خطوط الإنتاج الثلاثة. السؤال هو: أي خطوط الإنتاج الثلاثة تحقق أعلى إيرادات؟
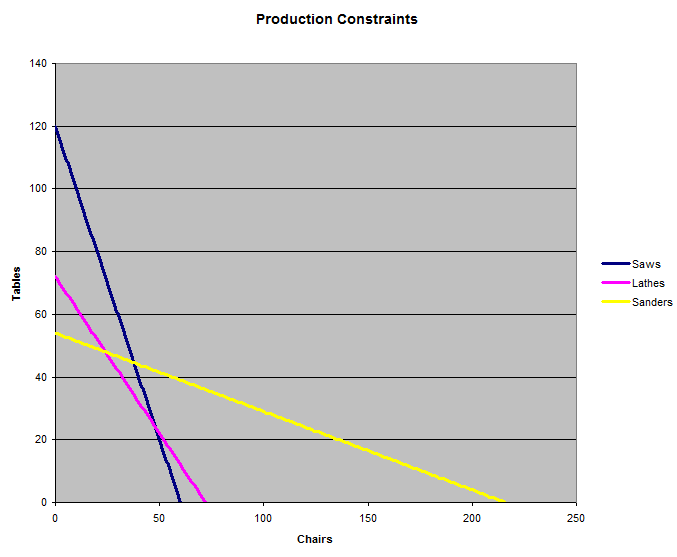
من المنطقي أن تكون الإجابة تقاطع خطين، أو صنع جميع الكراسي، أو صنع جميع الطاولات. لنحدد إذًا نقطة تقاطع الخطين. أولًا، لنحدد نقطة تقاطع المعادلتين (1) و(2). يمكننا تغيير تعبير <= إلى = فقط، لاستخدام الآلات بأقصى إمكاناتها.
(1) 10c + 5t = 600
(2) 5ج + 5ت = 360
اطرح (2) من (1):
5 ج = 240
ج = 48
إدخال 48 لـ c في المعادلة (1):
10×48 + 5t = 600
5t = 120
ت = 24
لذا، تلتقي المعادلتان (1) و(2) عند 48 كرسيًا و24 طاولة.
بعد ذلك، دعنا نجد مكان التقاء المعادلتين (2) و(3):
(2) 5ج + 5ت = 360
(3) 5 ج + 20 ت = 1080
طرح (2) من (3):
15 طن = 720
ت = 48
بوضع ذلك في (2) أو (3) يمكننا حل c، وهو 24.
وبالتالي، تلتقي المعادلتان (2) و(3) عند 24 كرسيًا و48 طاولة.
لا نحتاج إلى عناء البحث عن مكان التقاء المعادلتين (1) و(3)، لأننا نستطيع أن نرى من الرسم البياني أن مكان التقاء خطوط المنشار والصنفرة يقع خارج قيد المخرطة.
من الممكن أيضًا أن يكون صنع الكراسي فقط هو الإجابة الصحيحة. يوضح الرسم البياني أن المناشير هي أكبر عائق أمام صنع الكراسي فقط. من المعادلة (1)، إذا وضعنا 0 لعدد الطاولات، نحصل على c=60.
هناك احتمال آخر وهو صنع الطاولات فقط. يوضح الرسم البياني أن آلات الصنفرة ستشكل أكبر عائق. بإضافة صفر كراسي في المعادلة (3)، نجد أنه لا يمكن صنع أكثر من 54 طاولة.
يوضح الرسم البياني التالي إجمالي الإيرادات لكل إجابة ممكنة. تذكر أن الإيرادات هي ١٠ دولارات للكرسي و٢٠ دولارًا للطاولة.
إجمالي الإيرادات بالساعة
| الكراسي | الجداول | ربح |
| 0 | 54 | 1,080 دولارًا |
| 24 | 48 | 1200 دولار |
| 48 | 24 | 960 دولارًا |
| 60 | 0 | 600 دولار |
الملك لديه برميل ممتلئ بالنبيذ.
في ليلة الإثنين، يقوم أحد الخدم بسرقة ثلاثة أكواب من البرميل ويستبدلها بثلاثة أكواب من الماء.
في ليلة الثلاثاء، يسرق خادم آخر ثلاثة أكواب من برميل النبيذ المخفف ويستبدلها بثلاثة أكواب من الماء.
وفي ليلة الأربعاء، يسرق خادم آخر ثلاثة أكواب من برميل النبيذ المخفف ويستبدلها بثلاثة أكواب من الماء.
في صباح يوم الخميس يكون البرميل مكونًا من 50% نبيذ و 50% ماء.
ما هي كمية النبيذ التي كانت في البرميل في البداية؟
وهنا الجواب والحل (PDF).
لمناقشة هذه المشكلة، يرجى زيارة منتدياتي في Wizard of Vegas .
لو كان معي وعاءٌ فيه ٢٠٠ قطعة سكيتلز، و٣ منها كفيلةٌ بقتلي، فما احتمال موتي إذا تناولتُ حفنةً من ١٢ قطعةً وأكلتُها جميعاً؟ لنفترض أن قطعةً واحدةً سامةً من سكيتلز تكفي لقتلي.
لمزيد من المناقشة حول هذا السؤال، يرجى زيارة منتدياتي في Wizard of Vegas .
اختطف كائن فضائي عشرة منطقيين ووضعهم في غرفة. شرح لهم أنه سيرتبهم أولًا في صف، من الأطول إلى الأقصر، بحيث يواجه كل شخص اتجاه أقصر شخص يليه، ليتمكن كل شخص من رؤية جميع المنطقيين الأقصر، ولكن ليس الأطول. ثم شرح أنه سيضع قبعة سوداء أو بيضاء على كل شخص، ولكن لن يتمكن أحد من رؤية لون قبعته، بل قبعات المنطقيين الأقصر فقط. يمكن توزيع القبعات السوداء والبيضاء بأي عدد، وليس بالضرورة خمسة أو خمسة.
ثم يوضح الكائن الفضائي أنه سيسأل كل منطقي، بدءًا من الأطول، ثم تصاعديًا، عن لون قبعته. يمكن للمنطقيين سماع ردود من سبقوهم. باستثناء الإجابات بالأبيض والأسود، لا يُسمح لهم بالتواصل بأي شكل من الأشكال بعد بدء اللعبة. إذا أخطأ أكثر من منطقي واحد، فسيتم القضاء عليهم جميعًا. إذا كانت تسع إجابات صحيحة على الأقل، فسيتم إعادتهم سالمين إلى الأرض. ثم يمنحهم الكائن الفضائي بعض الوقت لوضع استراتيجية. ما هي استراتيجيتهم؟
فيما يلي استراتيجية ممكنة. اطلب من المنطقي الأول الذي سيبدأ بالتصرف أن يقول "أسود" إذا رأى عددًا زوجيًا من القبعات السوداء، و"أبيض" إذا رأى عددًا فرديًا من المنطقيين التسعة الآخرين. ستكون لديه فرصة 50% لمطابقة لون قبعته، لذا فهو الوحيد الذي يُحتمل أن يكون مخطئًا. أيًا كان ما سيقوله، عرّفه بأنه "اللون السائد".
بعد ذلك، سيُحصي المنطقي الثاني عدد القبعات السوداء على المنطقيين الثمانية الأقصر، ويطابقها مع لونٍ ما بنفس طريقة الفردي والزوجي التي استخدمها المنطقي الأول. إذا تطابقت هذه الألوان مع اللون الذي حدده المنطقي الأول، فيجب أن تكون لديه قبعة بيضاء، ويجب أن يُحدد اللون الأبيض. إذا لم تتطابق، فيجب أن تكون لديه قبعة سوداء، ويجب أن يُحدد اللون الأسود. إذا قال "أبيض"، فسيبقى اللون المُستخدم كما هو. إذا قال "أسود"، فسيُقلب اللون المُستخدم إلى اللون المُعاكس.
بعد ذلك، سيفعل المنطقي الثالث نفس ما فعله المنطقي الثاني، مع إحصاء القبعات السوداء للمنطقيين السبعة الأقصر. وبالمثل، إذا وافق على اللون الرئيسي، فسيقول "أبيض" ويبقى اللون الرئيسي كما هو. إذا لم يوافق على اللون الرئيسي، فسيقول "أسود" ويتغير اللون الرئيسي.
وسوف يفعل كل المنطقيين الآخرين نفس الشيء تمامًا.
بالطبع، يمكنهم بسهولة ربط اللون الأسود بمجموع فردي، والأبيض بمجموع زوجي. المهم هو اتفاقهم جميعًا على اللون الذي يُمثل أي تكافؤ فردي/زوجي. اتباع أيٍّ من الاستراتيجيتين سيؤدي إلى أن يكون جميع المنطقيين من الثاني إلى العاشر على صواب، وأن تكون احتمالية نجاح الأول ٥٠٪، وبالتالي سينجو جميعهم. هذه الاستراتيجية مناسبة لأي عدد من المنطقيين.
لدى كلٍّ من أكسل وبوب مجموعة أوراقه الخاصة المكونة من 52 ورقة. يخلطانها عشوائيًا. ثم يقلبان ورقةً واحدةً في كل مرة، في آنٍ واحد، من كل مجموعة. ما احتمال أن يقلبا الورقة نفسها في نفس الوقت مرةً واحدةً على الأقل؟
من السهل تقدير الإجابة كالتالي: ١-(٥١/٥٢) ٥٢ = ٠٫٦٣٥٦٨٦٤٨. مع ذلك، فإن التقديرات غير مُرضية عقليًا. لذا، دعونا نجد حلًا دقيقًا!
الخطوة ١: للبدء، احسب عدد طرق ترتيب المجموعة الثانية من البطاقات عندما تكون البطاقة الأولى رقم ١. الإجابة هي عدد طرق ترتيب البطاقات الـ ٥١ الأخرى، أي ٥١! = ١٥٥١١١٨٧٥٣٢٨٧٣٨٢٢٨٠٢٢٤٢٤٣٠١٦٤٦٩٣٠٣٢١١٠٦٣٢٥٩٧٢٠٠١٦٩٨٦١١٢٠٠٠٠٠٠٠٠٠٠٠.
يمكن لأي بطاقة أن تتطابق مع المجموعة الأولى، لذا يجب علينا تطبيق هذا على جميع البطاقات الـ 52. هذا يعطينا 52 × 51! = 52! مجموعة تتطابق فيها بطاقة واحدة على الأقل.
الخطوة ٢: مع ذلك، في الخطوة ١، نحسب مرتين كل حالة تتطابق فيها بطاقتان. على سبيل المثال، إذا كانت البطاقتان الأوليتان ١ و٢، فسنحسب ٥٠ طريقة لترتيب البطاقات الأخرى مرتين، مرة للبطاقة ١ كالبطاقة الأولى، ومرة ثانية للبطاقة ٢ كالبطاقة الثانية. عدد طرق اختيار بطاقتين من أصل ٥٢ هو combin(٥٢،٢) = ١٣٢٦. لكل مجموعة من بطاقتين، هناك ٥٠ طريقة لترتيب البطاقات الأخرى. لذلك، في الخطوة ٢، نحتاج إلى طرح combin(٥٢،٢)*٥٠! = (٥٢*٥١/٢!)*٥٠! = ٥٢!/٢! مجموعة.
الخطوة 3: لنفترض أن أول ثلاث بطاقات في المجموعة العشوائية هي 1، 2، و3 بالترتيب. هناك 49 طريقة لترتيب البطاقات الـ 49 الأخرى. كنا سنعدّها ثلاث مرات في الخطوة الأولى لاختيار بطاقة مطابقة واحدة على الأقل. ثم سنطرح جميع طرق الجمع (combin(3,2)=3 لاختيار بطاقتين من هذه البطاقات الثلاث في الخطوة الثانية. لذا، في هذه الحالة، كان سيتم عدّها 3-3=0، لذا نحتاج إلى إضافتها مرة أخرى. هناك حالات مثل الجمع (combin(52,3) لاختيار 3 بطاقات مطابقة على الأقل. لذا نحتاج إلى إضافة الجمع (combin(52,3)*49! = 52*51*50*49!/3! = 52!/3!).
الخطوة 4: بعد ذلك، ضع في اعتبارك الحالة التي تكون فيها البطاقات الأربع الأولى في المجموعة العشوائية هي 1 و2 و3 و4 بالترتيب. يوجد 48 طريقة لترتيب البطاقات الـ 48 الأخرى. كنا سنحسبها أربع مرات في الخطوة الأولى للعد بحثًا عن بطاقة مطابقة واحدة على الأقل. ثم كنا سنطرح جميع الطرق combin(4,2)=6 لاختيار بطاقتين من هذه البطاقات الأربع في الخطوة 2. ثم كنا سنضيف جميع الطرق combin(4,3)=4 لاختيار 3 بطاقات من هذه البطاقات الأربع. إذن لدينا 4-6 + 4 = طريقتان لعد كل حالة من هذه الحالات. لذا نحتاج إلى طرح إحدى هذه الطرق، بحيث يتم حساب كل حالة مرة واحدة. يوجد combin(52,4)*48! = 52*51*50*49*48!/4! = 52!/4! مثل هذه الحالات التي يجب إضافتها مرة أخرى.
سنستمر في القيام بذلك، بالتناوب بين الجمع والطرح لتصحيح العد المزدوج.
في النهاية، عدد الحالات التي تتطابق فيها بطاقة واحدة على الأقل من المجموعة العشوائية مع المجموعة المرتبة = combin(52,1)*51! - combin(52,2)*50! + combin(52,3)*49! - combin(52,4)*48! ... - combin(52,52)*1! = 52!/1! - 52!/2! + 52!/3! - 52!/4! ... - 52!/52! = x = 333239808909468890675694068318655265019682314241643033726180828783.
هناك 52! = y = 5271776154963652194226185415451226599692124538619822080000000000000 إجمالي الطرق لطلب 52 بطاقة.
وبالتالي، فإن الإجابة هي x/y = 0.6321205588285576784044762298
احتمال عدم وجود تطابقات هو 1-(x/y) = 0.3678794411714423215955237702.
إذا كان هذا الرقم يبدو مألوفًا، فيجب أن يكون كذلك. 1/e = 0.3678794411714423215955237702.
لذا، يمكن تقدير الإجابة بشكل وثيق للغاية على أنها 1-(1/e).
الشكر والتقدير
تم إجراء الحسابات الرياضية في Pari/GP
لقد تم طرح هذه المشكلة ومناقشتها في المنتدى الخاص بي في Wizard of Vegas .
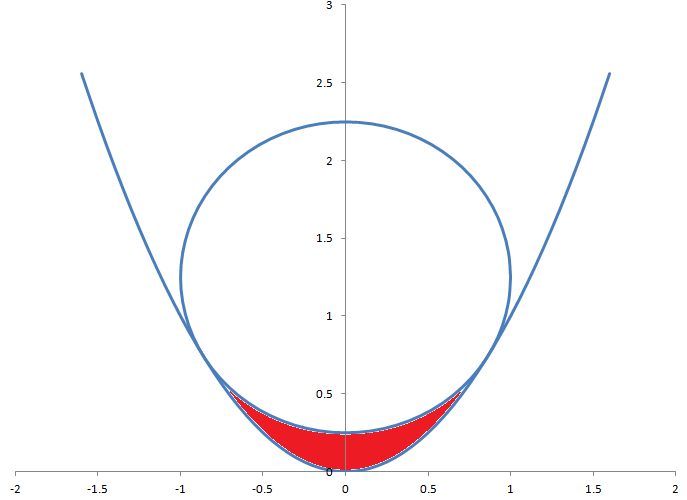
دائرة نصف قطرها ١ مماسة لقطع مكافئ معادلته ص = س ٢. ما مساحة المنطقة الحمراء بين الدائرة والقطع المكافئ؟
انقر على الزر أدناه للحصول على الإجابة.
هذا هو الحل الخاص بي. (PDF)
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
لقد حصلت على هذه المشكلة من Presh Talwalker من Mind Your Decisions .
يعمل موزع كازينو على نسخة جديدة من لعبة بوكر الثلاث أوراق. يأخذ جميع الأوراق ذات الوجوه من مجموعة أوراق قياسية ويخلطها جيدًا. ثم يوزع ثلاث أوراق على اللاعب رقم 1، وثلاث أوراق على اللاعب رقم 2، وثلاث أوراق على اللاعب رقم 3، والأوراق الثلاث الأخيرة على اللاعب رقم 4. ما احتمال أن تحتوي جميع الأيدي الأربع على ستريت (JQK من أي نوع)؟

الإجابة هي ٢١٦/٥٧٧٥ = تقريبًا ٠٫٠٣٧٤٠٢٥٩٧.
احتمال أن تكون اليد الأولى هي AKQ هو 1*(8/11)*(4/10) = 29.09%.
احتمال أن يكون عقرب الثواني هو AKQ، مع العلم أن العقرب الأول هو AKQ بالفعل، يساوي 1*(6/8)*(3/7) = 32.14%.
احتمال أن تكون اليد الثالثة هي AKQ، مع الأخذ في الاعتبار أن اليد الأولى والثانية هي بالفعل AKQ، يساوي 1*(4/5)*(2/4) = 40.00%
يجب أن تكون البطاقات المتبقية من نوع AKQ، نظرًا لأن الأيدي الثلاثة الأولى هي كذلك. وبالتالي، فإن الاحتمال هو حاصل ضرب الاحتمالات الثلاثة أعلاه، وهو ٢١٦/٥٧٧٥ = تقريبًا ٠٫٠٣٧٤٠٢٥٩٧.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
ما هو متوسط مساحة ومحيط المستطيل المرسوم عشوائيا داخل دائرة نصف قطرها 1؟
سؤال جيد. إليك إجاباتي:
وهنا حلي لكلا المشكلتين (PDF).
أوجد عددًا مكونًا من عشرة أرقام بحيث:
- الرقم الأول من العدد هو عدد الأصفار في العدد بأكمله.
- الرقم الثاني من العدد هو عدد 1 في العدد بأكمله.
- الرقم الثالث من العدد هو عدد 2 في العدد بأكمله.
- الرقم الرابع من العدد هو عدد 3 في العدد بأكمله.
- الرقم الخامس من العدد هو عدد الأرقام 4 في العدد بأكمله.
- الرقم السادس من العدد هو عدد 5 في العدد بأكمله.
- الرقم السابع من العدد هو عدد الستة في العدد بأكمله.
- الرقم الثامن من العدد هو عدد السبعات في العدد بأكمله.
- الرقم التاسع من العدد هو عدد الـ 8 في العدد بأكمله.
- الرقم العاشر من العدد هو عدد التسعة في العدد بأكمله.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
يتم توزيع ثلاث نقاط بشكل عشوائي وموحد على طول دائرة نصف قطرها 1. ما هي المسافة الدنيا المتوقعة بين النقاط الثلاث، حيث يتم قياس المسافات على طول المحيط؟
وهنا الحل الخاص بي (PDF).
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
يستغرق أليس وبيل ثلاث ساعات لطلاء المنزل.
يستغرق أليس وسيندي 4 ساعات لطلاء المنزل.
يستغرق بيل وسيندي 5 ساعات لطلاء المنزل.
كم من الوقت يستغرق الأمر إذا قاموا جميعًا بالرسم؟
وهنا الحل الخاص بي (PDF).


