على هذه الصفحة
لماذا عدد الأوراق مهم في لعبة البلاك جاك
مقدمة
أي مصدر موثوق في لعبة البلاك جاك سيؤكد وجود علاقة طردية بين عدد أوراق اللعب المستخدمة وميزة الكازينو، مع ثبات جميع العوامل الأخرى. بمعنى آخر، كلما قلّت أوراق اللعب، زادت احتمالات فوز اللاعب الهواة. هذه الحقيقة معروفة لدى لاعبي البلاك جاك الذين يمتلكون على الأقل المعرفة الكافية للبحث عن لعبة بقواعد جيدة. مع ذلك، لم أرَ قط دراسة متعمقة لسبب ذلك. الغرض من هذه المقالة هو تسليط الضوء على هذا السؤال.
قبل البدء، دعوني أضع بعض القواعد الأساسية. تم اختيار هذه القواعد لتكون واقعية قدر الإمكان بالنظر إلى ظروف البلاك جاك وقت كتابة هذه السطور في عام ٢٠٢٠:
- الموزع يضرب 17 ناعمة.
- تدفع لعبة البلاك جاك 3 إلى 2.
- يقوم الموزع بمراقبة البلاك جاك مع وجود عشرة أو الآس في المقدمة.
- يحق للاعب مضاعفة الرهان على أي بطاقتين.
- لا يجوز للاعب الاستسلام.
- يحق للاعب مضاعفة الرهان بعد التقسيم.
- يحق للاعب إعادة تقسيم أي زوج (بما في ذلك الآسات) حتى ثلاث مرات.
- يتم استخدام جهاز خلط مستمر (يتم خلط البطاقات بعد كل يد).
- يستخدم اللاعب استراتيجية أساسية.
تشير حاسبة حافة المنزل في لعبة البلاك جاك الخاصة بي بموجب هذه القواعد إلى أن حافة المنزل تكون على النحو التالي، وفقًا لعدد مجموعات البطاقات:
ميزة الكازينو في لعبة البلاك جاك حسب ديكس
| الطوابق | حافة المنزل |
|---|---|
| 1 | 0.014% |
| 2 | 0.341% |
| 4 | 0.499% |
| 6 | 0.551% |
| 8 | 0.577% |
قد لا تتفق هذه الأرقام تمامًا مع مصادر موثوقة أخرى في لعبة البلاك جاك. أعتقد أن أي اختلافات تُعزى إما إلى استخدام بطاقة مقطوعة أو إلى اتباع اللاعب لاستراتيجية مثالية تعتمد على التركيب. في المقابل، أفترض أن البطاقات تُخلط بعد كل جولة، وأن اللاعب يتبع دائمًا استراتيجية أساسية تعتمد على المجموع الكلي.
لاحظ أن فرق ميزة الكازينو هو 0.563% بين ثماني مجموعات ورق ومجموعة ورق واحدة. ستسعى هذه المقالة إلى الإجابة على سؤال لماذا يؤثر عدد مجموعات الورق بهذا القدر الكبير على احتمالات الفوز.
لعبة متوازنة
كنقطة بداية، أفترض لعبة بلاك جاك مبسطة، حيث تكون قواعدها متطابقة تمامًا لكل من اللاعب والموزع، مما ينتج عنه هامش ربح للكازينو بنسبة 0% بغض النظر عن عدد أوراق اللعب. ثم أضيف تدريجيًا قواعد البلاك جاك الفعلية، واحدة تلو الأخرى، وأدرس تأثيرها على هامش الربح للكازينو حسب عدد أوراق اللعب.
يجب أن تكون للعبة البلاك جاك المبسطة الافتراضية الأولية نفس القواعد المذكورة سابقًا، باستثناء:
- يتبع اللاعب استراتيجية "تقليد الموزع".
- الفوز في لعبة البلاك جاك يدفع مبلغًا متساويًا من المال.
- إذا خسر كل من اللاعب والموزع، فإن النتيجة هي التعادل.
من الواضح أن حافة المنزل في هذه اللعبة المتوازنة هي 0.000% بالضبط، لأن كل قاعدة تنطبق على كلا الجانبين بالتساوي.
ميزة موقع التاجر
من يفوز في البلاك جاك عندما يخسر كلٌّ من اللاعب والموزع؟ الموزع هو الفائز. بمعنى آخر، يتمتع الموزع بميزة موقعية، حيث يخسر أول من يخسر، ويتعيّن على اللاعب التصرف أولاً. وهذا هو سبب تمتع الموزع بالميزة، على الرغم من وجود العديد من القواعد التي تُعيق اللاعب. إضافة هذه القاعدة إلى لعبة التوازن وتطبيقها من خلال محاكاة لمجموعات أوراق واحدة وثمانية يُنتج عنه العوائد المتوقعة التالية للاعب.
القيم المتوقعة حسب تغيير القاعدة
| قاعدة | سطح واحد | ثمانية طوابق | اختلاف |
|---|---|---|---|
| ميزة موقع التاجر | -8.237% | -8.157% | -0.079% |
يوضح الجدول أعلاه أن احتمالات فوز اللاعب في هذه اللعبة الافتراضية التي تتضمن مجموعة أوراق واحدة أقل من احتمالات فوزه بثماني مجموعات أوراق. ويرجع ذلك إلى أنه كلما انخفض عدد مجموعات الأوراق، زاد احتمال الخسارة. فيما يلي احتمال الخسارة في لعبة "محاكاة الموزع"، بافتراض أن الموزع سيلعب أوراقه حتى لو خسر اللاعب أولاً.
- سطح واحد = 27.333%
- ثمانية طوابق = 27.209%
يوضح ما سبق أن احتمالية خسارة أيٍّ من الطرفين أعلى بنسبة 0.124% في لعبة ذات مجموعة أوراق واحدة مقارنةً بثمانية مجموعات أوراق. هناك علاقة بين خسارة كلٍّ من الطرفين، لذا دعونا نلقي نظرة على التركيبات الأربع لخسارة اللاعب والموزع:
احتمالات الفشل
| تمثال نصفي للاعب | القبض على تاجر | سطح واحد | ثمانية طوابق | اختلاف |
|---|---|---|---|---|
| لا | لا | 44.096% | 44.468% | -0.372% |
| لا | نعم | 19.095% | 19.051% | 0.044% |
| نعم | لا | 19.095% | 19.051% | 0.044% |
| نعم | نعم | 8.237% | 8.157% | 0.079% |
| المجموع | 90.524% | 90.728% | -0.204% |
السبب في أن الاحتمالات لا تصل إلى 100٪ هو أن الطاولة لا تحسب تلك الأيدي التي يكون فيها أي من الجانبين لديه بلاك جاك ولم يتم لعب اليد بطريقة أخرى. يوضح صف "نعم نعم" المواقف التي يخسر فيها كلا الجانبين، مما يؤدي إلى فوز الموزع. يوضح ذلك حدوث ذلك بنسبة 0.080٪ أكثر في لعبة ذات مجموعة واحدة مقارنة بثمانية مجموعات. لماذا؟ إذا خسر أي من الجانبين، فلا بد أن يكون ذلك بعد الحصول على يد قوية من 12 إلى 16 نقطة. يجب أن تتكون هذه اليد من ورقتين على الأقل. وفي الوقت نفسه، إذا كان لدى أي من الجانبين ورقتان عاليتا القيمة، فستقف. بمعنى آخر، يحدث الضرب عمومًا بأيدي تحتوي على بطاقات أصغر من القيمة المتوسطة. يؤدي إزالة البطاقات الصغيرة في مواقف الضرب إلى وجود فائض من البطاقات العالية في البطاقات المتبقية. يكون تأثير إزالة البطاقات الصغيرة قبل الخسارة أكثر أهمية في لعبة ذات مجموعة واحدة.
بلاك جاك يدفع 3 إلى 2
القاعدة التالية التي سنضيفها إلى اللعبة المتوازنة هي أن اللاعب الفائز بالبلاك جاك يدفع 3 إلى 2. بإضافة هذه القاعدة إلى محاكاتي، نحصل على العائدات التراكمية المتوقعة للاعب.
- مجموعة واحدة = -5.912%
- ثمانية طوابق = -5.894%
جدول نتائج المحاكاة لإضافة صف لإضافة هذه القاعدة هو:
القيم المتوقعة حسب تغيير القاعدة
| قاعدة | سطح واحد | ثمانية طوابق | اختلاف |
|---|---|---|---|
| ميزة موقع التاجر | -8.237% | -8.157% | -0.079% |
| اللاعب الفائز في لعبة البلاك جاك يدفع 3 إلى 2 | -5.912% | -5.894% | -0.018% |
إن أخذ الفرق بين الصفّين يُظهر الفائدة التي تعود على اللاعب من فوز بلاك جاك بقيمة 3 إلى 2:
- سطح واحد = 2.325%
- ثمانية طوابق = 2.263%
- الفرق = 0.062%
من السهل التحقق من ذلك رياضيًا، كما يلي. لنفترض أن d = عدد أوراق اللعب. باستخدام صيغة Excel، يكون احتمال فوز بلاك جاك هو: الاحتمال (بلاك جاك اللاعب) * (1-احتمال (بلاك جاك الموزع)) = (16*d)*(4*d)/المجموع(52*d,2) * [1-(16*d-1)*(4*d-1)/المجموع(52*d-2,2)
احتمالية الفوز في لعبة البلاك جاك
| الطوابق | احتمال |
|---|---|
| 1 | 4.649% |
| 2 | 4.578% |
| 4 | 4.544% |
| 6 | 4.532% |
| 8 | 4.527% |
كما هو موضح أعلاه، يزداد احتمال الفوز في لعبة بلاك جاك مع انخفاض عدد مجموعات الأوراق. ويعود ذلك ببساطة إلى آثار الإزالة. على سبيل المثال، لنفترض أن أول بطاقة للاعب هي أي بطاقة بقيمة 10. يكون احتمال ذلك 4/13، بغض النظر عن عدد مجموعات الأوراق. من السهل ملاحظة أنه في لعبة ذات مجموعة أوراق واحدة، يكون احتمال الحصول على آس كالبطاقة الثانية 4/51 = 7.843%. أما في لعبة ذات ثماني مجموعات أوراق، فيكون هذا الاحتمال 32/415 = 7.711%، وهو أقل بنسبة 0.123% من لعبة ذات مجموعة أوراق واحدة. ببساطة، سبب ارتفاع احتمال الحصول على الآس في لعبة ذات مجموعة أوراق واحدة هو أن المجموعة تصبح أغنى بالآسات بعد إزالة 10 منها. وينطبق الشيء نفسه إذا كانت البطاقة الأولى آسًا؛ ستكون البطاقات المتبقية أغنى بالعشرات في لعبة ذات مجموعة أوراق واحدة.
علاوة على ذلك، إذا حصل اللاعب على بلاك جاك، فإن احتمال حصول الموزع عليه ينخفض مع انخفاض عدد مجموعات الأوراق. ويرجع ذلك إلى أن إزالة اللاعب لآس وعشرة من مجموعة أوراق اللعب في لعبة ذات مجموعة أوراق لعب واحدة يجعل حصول الموزع على بلاك جاك أصعب بكثير مقارنةً بلعبة ذات ثماني مجموعات أوراق لعب. وبشكل أكثر تحديدًا، فإن احتمال حصول الموزع على بلاك جاك، بافتراض أن اللاعب لديه بلاك جاك بالفعل، هو 3.673% مع مجموعة أوراق لعب واحدة و4.605% مع ثماني مجموعات أوراق لعب. يربح اللاعب نصف وحدة إضافية مع كل بلاك جاك فائز. للحصول على قيمة عائد ربح بلاك جاك بنسبة 3-2 في لعبتنا الافتراضية المتوازنة، احسب احتمال فوز بلاك جاك واضربه في 0.5 لنصف الوحدة الإضافية في كل مرة. ينتج عن ذلك ميزة للاعب حسب عدد مجموعات الأوراق كما يلي:
ميزة اللاعب في الفوز بالبلاك جاك
| الطوابق | حافة اللاعب |
|---|---|
| 1 | 2.325% |
| 2 | 2.289% |
| 4 | 2.272% |
| 6 | 2.266% |
| 8 | 2.263% |
لاحظ أن الفوائد المحسوبة رياضيا للاعب الفائز في لعبة البلاك جاك الذي يدفع نصف وحدة إضافية تتطابق مع نتائج المحاكاة التي تم عرضها سابقًا للبطاقات ذات المجموعة الواحدة والثمانية.
يوضح الجدول أدناه قائمة تشغيل للقواعد التي تم تحليلها حتى هذه النقطة وفائدتها للاعب الذي يستخدم مجموعة أوراق واحدة مقارنة بلاعب الذي يستخدم ثماني مجموعات أوراق:
تأثير القواعد
| قاعدة | ميزة الطابق الواحد |
|---|---|
| ميزة موقع التاجر | -0.079% |
| اللاعب الفائز في لعبة البلاك جاك يدفع 3 إلى 2 | 0.062% |
| المجموع | -0.018% |
بعد ذلك، دعونا نحلل فائدة السماح للاعب بالوقوف على مجموع صعب يتراوح بين ١٢ و١٦. الاستراتيجية الأساسية المعتمدة على المجموع في هذا النطاق هي نفسها لأي عدد من المجموعات، كما يلي:
- مع مجموع 12، قف ضد الموزع 4 إلى 6، وإلا فاضرب.
- مع مجموع 13 إلى 16، قف ضد الموزع 2 إلى 6، وإلا فاضرب.
تؤدي إضافة هذه الاستراتيجية إلى نتائج المحاكاة إلى العوائد المتوقعة للاعب التالية:
- سطح واحد = -2.209%
- ثمانية طوابق = -2.625%
يتضمن جدول نتائج المحاكاة أدناه صفًا لإضافة هذه القاعدة:
القيم المتوقعة حسب تغيير القاعدة
| قاعدة | سطح واحد | ثمانية طوابق | اختلاف |
|---|---|---|---|
| ميزة موقع التاجر | -8.237% | -8.157% | -0.079% |
| اللاعب الفائز في لعبة البلاك جاك يدفع 3 إلى 2 | -5.912% | -5.894% | -0.018% |
إن أخذ الفرق بين الصف الثاني والثالث يظهر تأثير إرادة اللاعب الحرة في الوقوف على 12 إلى 16 صعبة.
- سطح واحد = 3.703%
- ثمانية طوابق = 3.270%
- الفرق = 0.433%
بحساب الفرق بين هذين الرقمين، يتضح أن تأثير تغيير هذه القاعدة يزيد بنسبة 0.433% للاعب في لعبة ذات مجموعة أوراق واحدة مقارنةً بثمانية مجموعات أوراق. وخلافًا للاعتقاد الشائع، يُفسر هذا في الغالب سبب زيادة قيمة لعبة ذات مجموعة أوراق واحدة بنسبة 0.563% للاعب مقارنةً بلعبة ذات ثمانية مجموعات أوراق.
بالنظر بشكل أعمق إلى ما يحدث عندما يقف اللاعب على مجموعات صلبة من 12 إلى 16، بينما لا يستطيع الموزع ذلك ‒ يوضح هذا الجدول الفائدة التي تعود على اللاعب من الأحداث المختلفة التي تتغير بسبب حصول اللاعب على مجموعات صلبة أقل، مما يؤدي إلى عدد أقل من حالات إفلاس اللاعبين، والمزيد من حالات إفلاس الموزع، بالإضافة إلى خسارة الموزع لمزيد من المواجهات:
النتائج المحتملة عندما يقف اللاعب على مستوى صلب من 12 إلى 16
| حدث | سطح واحد | ثمانية طوابق | اختلاف |
|---|---|---|---|
| عدد أقل من حالات التمثال النصفي للاعبين فقط | 6.282% | 6.271% | 0.010% |
| مزيد من حالات النصب والاحتيال على التجار فقط | 4.228% | 4.171% | 0.057% |
| أقل من كلا التمثالين | 4.228% | 4.172% | 0.055% |
| يفوز اللاعب بعدد أقل من المواجهات | -1.914% | -2.039% | 0.125% |
| يفوز الموزع بمزيد من المواجهات | -9.121% | -9.306% | 0.185% |
| المجموع | 3.703% | 3.270% | 0.433% |
تم تبسيط نفس الجدول لإظهار فائدة الفوز أكثر بسبب فشل الموزع في كثير من الأحيان وخسارته المزيد من المواجهات:
ملخص النتائج المحتملة عندما يقف اللاعب على مستوى صلب من 12 إلى 16
| حدث | سطح واحد | ثمانية طوابق | اختلاف |
|---|---|---|---|
| اللاعب الذي يكسر فائدة أقل | 14.738% | 14.615% | 0.123% |
| خسارة المواجهة | -11.035% | -11.345% | 0.310% |
| المجموع | 3.703% | 3.270% | 0.433% |
ببساطة، في لعبة ذات مجموعة أوراق واحدة، يُخسر اللاعب 14.738% أقل من الموزع باتباع استراتيجية أساسية بمجموع صعب يتراوح بين 12 و16. مع ذلك، في 75% من هذه الأيدي، لا يُخسر الموزع، مما يؤدي إلى فوز الموزع في مواجهة مع يد لاعب بمجموع 16 أو أقل لا يمكنها الفوز. مقارنةً بجميع الأيدي، يوفر اللاعب 14.738% بخسارة أقل، لكنه يُعيد 11.035% على شكل خسائر مواجهة أكثر، محققًا ربحًا صافيًا قدره 3.703% في لعبة ذات مجموعة أوراق واحدة.
هذه الفائدة لا تتجاوز 3.270% في لعبة بثمانية مجموعات أوراق. وبالنظر إلى كل شيء، فإن فائدة الترتيب الاستراتيجي على البطاقات من 12 إلى 16 تزيد بنسبة 0.433% للاعب في لعبة بالمجموعة الواحدة مقارنةً بثمانية مجموعات أوراق.
لماذا يُعدّ الموقف الاستراتيجي أكثر قيمة في مجموعة أوراق واحدة مقارنةً بثمانية مجموعات؟ الإجابة مشابهة لإجابة لماذا تكون ميزة الموزع في الموقع أكثر أهمية في لعبة المجموعة الواحدة. هناك المزيد من الخسائر في لعبة المجموعة الواحدة. على الرغم من أن الخسائر الأكبر يمكن أن تكون ذات فائدة للطرفين، إلا أنها تؤثر على اللاعب بشكل أكبر لأنه يخسر عندما ينكسر كلا الجانبين. من المرجح أن تتكون هذه المجموعات من 12 إلى 16 عندما يقف اللاعب من أوراق صغيرة أكثر من الكبيرة. هذا يترك المزيد من الأوراق العالية المتبقية في المجموعة مما قد يؤدي إلى خسارة اللاعب. تكون آثار إزالة هذه الأوراق المنخفضة التي يحتاجها اللاعب لتحسين يده أكثر تكلفة في لعبة المجموعة الواحدة منها في لعبة الثمانية مجموعات. بمعنى آخر، يُعدّ الحصول على أوراق صلبة أكثر خطورة في لعبة المجموعة الواحدة. بدلاً من ذلك، يكون الوقوف أكثر فائدة في لعبة المجموعة الواحدة.
فيما يلي جدول محدث للتكلفة والفائدة لكل تغيير في القواعد:
تأثير القواعد
| قاعدة | ميزة الطابق الواحد |
|---|---|
| ميزة موقع التاجر | -0.079% |
| اللاعب الفائز في لعبة البلاك جاك يدفع 3 إلى 2 | 0.061% |
| يجوز للاعب الوقوف على 12 إلى 16 صلبة | 0.433% |
| المجموع | 0.415% |
يجوز للاعب أن يضاعف
الآن، لنحلل فائدة السماح للاعب بمضاعفة الرهان. لدراسة هذا التأثير، طلبتُ من المحاكاة اتباع استراتيجية المضاعفة المناسبة لعدد أوراق اللعب المحددة، والتي سنتناولها لاحقًا في هذه المقالة. تُنتج إضافة هذه الاستراتيجية إلى المحاكاة العوائد المتوقعة للاعب التالية:
- مجموعة واحدة = -0.556%
- ثمانية طوابق = -1.245%
يتضمن جدول نتائج المحاكاة هذا صفًا لإضافة هذه القاعدة:
القيم المتوقعة حسب تغيير القاعدة
| قاعدة | سطح واحد | ثمانية طوابق | اختلاف |
|---|---|---|---|
| ميزة موقع التاجر | -8.237% | -8.157% | -0.079% |
| اللاعب الفائز في لعبة البلاك جاك يدفع 3 إلى 2 | -5.912% | -5.894% | -0.018% |
| يجوز للاعب الوقوف على 12 إلى 16 صلبة | -2.209% | -2.625% | 0.415% |
| يجوز للاعب مضاعفة | -0.556% | -1.245% | 0.689% |
الفرق بين الصف الثالث والرابع يظهر تأثير حرية الإرادة لدى اللاعب في المضاعفة، كما يلي:
- سطح واحد = 1.653%
- ثمانية طوابق = 1.380%
- الفرق = 0.273%
بحساب الفرق بين هذين الرقمين، يتضح أن تأثير تغيير هذه القاعدة يزيد بنسبة 0.273% للاعب في لعبة ذات مجموعة أوراق واحدة مقارنةً بثمانية مجموعات أوراق. وهذا يفسر جزءًا مهمًا آخر من سبب زيادة قيمة لعبة ذات مجموعة أوراق واحدة بنسبة 0.563% للاعب مقارنةً بلعبة ذات ثمانية مجموعات أوراق.
لماذا يُعدّ المضاعفة أكثر قيمة في لعبة ذات مجموعة أوراق لعب واحدة؟ في أغلب الأحيان، عندما يضاعف اللاعب، يكون ذلك بمجموع صعب يتراوح بين 9 و11 نقطة. تُجرى المضاعفة ببطاقتين، لذا يجب إضافة بطاقتين أصغر من المتوسط إلى مجموع منخفض يتراوح بين 9 و11 نقطة. إذا أُزيلت بطاقتان صغيرتان من مجموعة أوراق لعب واحدة، فإن احتمالية أن تكون البطاقة التالية عشرة هي 32.00%، وهي نسبة جيدة بالطبع عند المضاعفة بمجموع صعب. في المقابل، إذا أُزيلت بطاقتان صغيرتان من مجموعة أوراق لعب من ثماني مجموعات، فإن تأثير الإزالة يكون أقل قوة، مما يقلل من احتمالية أن تكون البطاقة التالية عشرة إلى 30.92%.
فيما يلي جدول مُحدّث لتكلفة/فائدة كل تغيير في القواعد. يُرجى ملاحظة أن الفائدة الإجمالية البالغة 0.689% تتجاوز الفرق النهائي في هامش ربح الكازينو. وذلك لأننا لم نأخذ في الاعتبار بعد تأثير التقسيم.
تأثير القواعد
| قاعدة | ميزة الطابق الواحد |
|---|---|
| ميزة موقع التاجر | -0.079% |
| اللاعب الفائز في لعبة البلاك جاك يدفع 3 إلى 2 | 0.061% |
| يجوز للاعب الوقوف على 12 إلى 16 صلبة | 0.433% |
| يجوز للاعب مضاعفة | 0.273% |
| المجموع | 0.689% |
قد ينقسم اللاعب
بعد ذلك، قمتُ بتحليل فائدة السماح للاعب بالتقسيم. لدراسة هذا التأثير، جعلتُ المحاكاة تتبع استراتيجية التقسيم المناسبة لعدد أوراق اللعب المحددة، والتي ستُعرض لاحقًا في المقالة. بإضافة هذه الاستراتيجية، نصل إلى الاستراتيجية الأساسية الكاملة. لا توجد أي اختلافات أخرى في القواعد بين اللاعب والموزع للدراسة بعد إضافة التقسيم. العائدات المتوقعة للاعب من الاستراتيجية الأساسية الكاملة هي:
- سطح واحد = -0.012%
- ثمانية طوابق = -0.575%
جدول نتائج المحاكاة بما في ذلك صف لإضافة هذه القاعدة هو:
القيم المتوقعة حسب تغيير القاعدة
| قاعدة | سطح واحد | ثمانية طوابق | اختلاف |
|---|---|---|---|
| ميزة موقع التاجر | -8.237% | -8.157% | -0.079% |
| اللاعب الفائز في لعبة البلاك جاك يدفع 3 إلى 2 | -5.912% | -5.894% | -0.018% |
| يجوز للاعب الوقوف على 12 إلى 16 صلبة | -2.209% | -2.625% | 0.415% |
| يجوز للاعب مضاعفة | -0.556% | -1.245% | 0.689% |
| يجوز للاعب الانقسام | -0.012% | -0.575% | 0.563% |
الفرق بين الصف الرابع والخامس يظهر تأثير حرية إرادة اللاعب في الانقسام.
- سطح واحد = 0.544%
- ثمانية طوابق = 0.669%
- الفرق = -0.125%
يُظهر الفرق بين الرقمين أن تأثير تغيير هذه القاعدة أقل بنسبة 0.125% بالنسبة للاعب في لعبة ذات مجموعة أوراق واحدة مقارنة بلعبة ذات ثماني مجموعات أوراق.
السبب في أن تقسيم البطاقات أكثر فائدة في لعبة بثمانية مجموعات من البطاقات مقارنةً بلعبة واحدة، هو أن فرص الحصول على زوج من البطاقات في أول بطاقتين أكبر. تحديدًا، في لعبة بثمانية مجموعات من البطاقات، وباستخدام مصطلحات إكسل، يكون الاحتمال 13*comb(4*8,2)/comb(52*8,2) = 7.470%. أما في لعبة بالمجموعة الواحدة، فيكون الاحتمال 13*comb(4*1,2)/comb(52*1,2) = 5.882%.
تذكر أيضًا أن قواعد اللعبة الأساسية تسمح بإعادة تقسيم البطاقات حتى ثلاث مرات أو حتى أربع أيادٍ. إذا أُزيلت بطاقتان من نفس الرتبة من مجموعة أوراق واحدة، فإن احتمالية الحصول على نفس الرتبة في البطاقة التالية هي 2/50 = 4.000%. أما في لعبة بثمانية مجموعات أوراق، فإن هذا الاحتمال هو 30/414 = 7.246%. مع قلة التقسيم وإعادة التقسيم في لعبة بمجموعة أوراق واحدة، تقل قيمة التقسيم الإجمالية. وهذا يفسر انخفاض فائدة التقسيم بالانتقال من ثماني مجموعات أوراق إلى مجموعة أوراق واحدة.
إن إضافة التأثير السلبي للتقسيم إلى اللعبة ذات المجموعة الواحدة يكمل جدولنا لتأثير القواعد المختلفة على فائدة اللعبة ذات المجموعة الواحدة مقارنة باللعب بثمانية مجموعات.
القاعدة: مجموعة أوراق واحدة: ميزة الموزع: -0.079%: يدفع اللاعب الفائز في البلاك جاك من 3 إلى 2. 0.061%: يجوز للاعب التوقف عند أوراق صلبة من 12 إلى 16. 0.433%: يجوز للاعب المضاعفة. 0.273%: يجوز للاعب التقسيم. -0.125%: الإجمالي. 0.563%:لاحظ أن مجموع النسبة في الخلية اليمنى السفلية، والبالغة 0.563%، يطابق الفروقات التي أعطتها حاسبة هامش الكازينو المذكورة في بداية المقال. إليك الجدول نفسه مُدرجًا حسب ترتيب تأثيره:
تأثير القواعد
| قاعدة | ميزة الطابق الواحد |
|---|---|
| ميزة موقع التاجر | -0.079% |
| اللاعب الفائز في لعبة البلاك جاك يدفع 3 إلى 2 | 0.061% |
| يجوز للاعب الوقوف على 12 إلى 16 صلبة | 0.433% |
| يجوز للاعب مضاعفة | 0.273% |
| يجوز للاعب الانقسام | -0.125% |
| المجموع | 0.563% |
جداول الاستراتيجية الأساسية
يوضح الجدول التالي الإستراتيجية الأساسية المناسبة للقواعد المذكورة وأحد المجموعات.
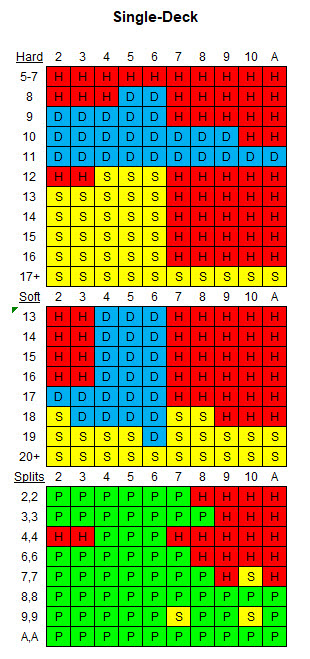
يوضح الجدول التالي الاستراتيجية الأساسية المناسبة للقواعد المذكورة والثمانية مجموعات من الأوراق.
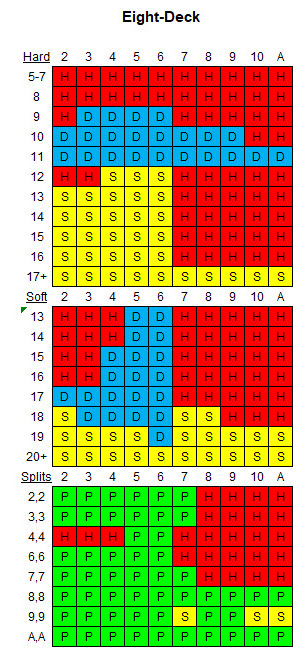
جداول القيمة المتوقعة
يوضح الجدول التالي القيمة المتوقعة لكل يد أولى في لعبة المجموعة الواحدة. يُظهر الصف العلوي ورقة الموزع المكشوفة. تُقاس القيم المتوقعة قبل أن يتحقق الموزع من وجود بلاك جاك. يُظهر عمود الإجمالي المتوسط المرجح للقيم المتوقعة في كل صف وفقًا لاحتمالية الحصول على اليد. تُظهر الخلية السفلية اليمنى القيمة المتوقعة للعبة بأكملها.
القيم المتوقعة في لعبة ذات طابق واحد
القيم المتوقعة حسب يد اللاعب مقابل بطاقة الموزع المفتوحة مع مجموعة واحدة
| لاعب | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | بارِع | المجموع |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | -0.1278 | -0.0968 | -0.0379 | 0.0227 | 0.0403 | -0.1191 | -0.1805 | -0.2624 | -0.3654 | -0.5443 | -0.2169 |
| 6 | -0.1477 | -0.1037 | -0.0519 | 0.0104 | 0.0371 | -0.1640 | -0.2343 | -0.3046 | -0.4015 | -0.5713 | -0.2469 |
| 7 | -0.1120 | -0.0701 | -0.0119 | 0.0528 | 0.0683 | -0.0690 | -0.2232 | -0.2948 | -0.3863 | -0.5765 | -0.2211 |
| 8 | -0.0174 | 0.0199 | 0.0826 | 0.1407 | 0.1498 | 0.0921 | -0.0565 | -0.2135 | -0.3136 | -0.5144 | -0.1286 |
| 9 | 0.1124 | 0.1923 | 0.2837 | 0.3753 | 0.3799 | 0.1951 | 0.1111 | -0.0519 | -0.2165 | -0.4146 | 0.0151 |
| 10 | 0.4262 | 0.4908 | 0.5494 | 0.6276 | 0.6241 | 0.4458 | 0.3145 | 0.1644 | -0.0528 | -0.2991 | 0.2316 |
| 11 | 0.5428 | 0.5922 | 0.6516 | 0.7176 | 0.7198 | 0.4785 | 0.3417 | 0.2240 | 0.0670 | -0.1848 | 0.3268 |
| 12 | -0.2518 | -0.2255 | -0.1915 | -0.1364 | -0.1194 | -0.2273 | -0.2925 | -0.3639 | -0.4175 | -0.5824 | -0.3131 |
| 13 | -0.2879 | -0.2411 | -0.1816 | -0.1344 | -0.1208 | -0.2861 | -0.3461 | -0.3764 | -0.4590 | -0.6106 | -0.3415 |
| 14 | -0.2900 | -0.2391 | -0.1835 | -0.1342 | -0.1209 | -0.3442 | -0.3612 | -0.4192 | -0.4957 | -0.6356 | -0.3644 |
| 15 | -0.2803 | -0.2379 | -0.1837 | -0.1388 | -0.1266 | -0.3590 | -0.4133 | -0.4703 | -0.5397 | -0.6677 | -0.3893 |
| 16 | -0.2863 | -0.2446 | -0.1872 | -0.1435 | -0.1450 | -0.3760 | -0.4254 | -0.4797 | -0.5482 | -0.6739 | -0.3978 |
| 17 | -0.1568 | -0.1216 | -0.0712 | -0.0445 | -0.0306 | -0.1217 | -0.3976 | -0.4154 | -0.4562 | -0.6560 | -0.2947 |
| 18 | 0.1072 | 0.1359 | 0.1538 | 0.1983 | 0.2031 | 0.3887 | 0.0956 | -0.1961 | -0.2242 | -0.4527 | -0.0185 |
| 19 | 0.3763 | 0.3774 | 0.3965 | 0.4449 | 0.4364 | 0.6101 | 0.5769 | 0.2642 | 0.0125 | -0.1586 | 0.2644 |
| أ،2 | 0.0402 | 0.0711 | 0.1174 | 0.2130 | 0.2455 | 0.1074 | 0.0392 | -0.0141 | -0.1454 | -0.3991 | -0.0057 |
| أ،3 | 0.0184 | 0.0447 | 0.1127 | 0.2042 | 0.2391 | 0.0605 | 0.0349 | -0.0602 | -0.1781 | -0.4205 | -0.0308 |
| أ،4 | -0.0103 | 0.0237 | 0.0892 | 0.1753 | 0.2191 | 0.0339 | -0.0354 | -0.1136 | -0.2226 | -0.4533 | -0.0697 |
| أ،5 | -0.0298 | -0.0019 | 0.0667 | 0.1490 | 0.2327 | -0.0239 | -0.0842 | -0.1666 | -0.2760 | -0.4900 | -0.1094 |
| أ،6 | 0.0142 | 0.0743 | 0.1549 | 0.2805 | 0.2630 | 0.0597 | -0.0646 | -0.1348 | -0.2383 | -0.4810 | -0.0586 |
| أ،7 | 0.1279 | 0.1867 | 0.3091 | 0.3482 | 0.3623 | 0.4118 | 0.1209 | -0.0873 | -0.1926 | -0.4433 | 0.0459 |
| أ،8 | 0.3953 | 0.4157 | 0.4100 | 0.4593 | 0.4666 | 0.6146 | 0.6078 | 0.2882 | -0.0009 | -0.1938 | 0.2686 |
| أ،9 | 0.6525 | 0.6415 | 0.6507 | 0.6810 | 0.6730 | 0.7732 | 0.7848 | 0.7656 | 0.4594 | 0.0943 | 0.5871 |
| أ،10 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.4081 | 1.0409 | 1.4449 |
| أ،أ | 0.6384 | 0.6863 | 0.7417 | 0.8075 | 0.8289 | 0.6277 | 0.4865 | 0.3605 | 0.2080 | -0.1580 | 0.4744 |
| 2,2 | -0.0349 | 0.0396 | 0.1235 | 0.3014 | 0.3378 | 0.0137 | -0.1412 | -0.2224 | -0.3355 | -0.5246 | -0.1145 |
| 3,3 | -0.1082 | -0.0209 | 0.1607 | 0.3049 | 0.3395 | -0.0448 | -0.2232 | -0.3100 | -0.3986 | -0.5715 | -0.1646 |
| 4,4 | -0.0136 | 0.0268 | 0.1354 | 0.2680 | 0.2980 | 0.1104 | -0.0549 | -0.2063 | -0.3069 | -0.5065 | -0.0991 |
| 5,5 | 0.4441 | 0.5075 | 0.5870 | 0.6933 | 0.7084 | 0.4663 | 0.3227 | 0.1738 | -0.0510 | -0.2978 | 0.2444 |
| 6,6 | -0.0963 | 0.0132 | 0.1456 | 0.2786 | 0.1992 | -0.1933 | -0.3222 | -0.3862 | -0.4366 | -0.5989 | -0.2245 |
| 7,7 | -0.0546 | 0.0494 | 0.1879 | 0.2244 | 0.2396 | -0.0524 | -0.3804 | -0.4744 | -0.5556 | -0.6790 | -0.2508 |
| 8,8 | 0.1165 | 0.1873 | 0.2245 | 0.3287 | 0.3508 | 0.3040 | -0.0599 | -0.4017 | -0.4929 | -0.6389 | -0.1224 |
| 9,9 | 0.2052 | 0.2156 | 0.3070 | 0.4064 | 0.4080 | 0.4011 | 0.2067 | -0.0986 | -0.2041 | -0.4520 | 0.0666 |
| 10,10 | 0.6220 | 0.6323 | 0.6402 | 0.6718 | 0.6683 | 0.7647 | 0.7832 | 0.7440 | 0.4539 | 0.1383 | 0.5803 |
| المجموع | 0.1021 | 0.1388 | 0.1860 | 0.2391 | 0.2471 | 0.1473 | 0.0551 | -0.0435 | -0.1712 | -0.3891 | -0.0001 |
القيم المتوقعة في لعبة مكونة من ثماني أوراق
القيم المتوقعة حسب يد اللاعب مقابل بطاقة الموزع المفتوحة مع ثماني مجموعات من الأوراق
| لاعب | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | بارِع | المجموع |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | -0.1258 | -0.0929 | -0.0562 | -0.0175 | 0.018 | -0.1196 | -0.1871 | -0.266 | -0.3663 | -0.5291 | -0.2191 |
| 6 | -0.1389 | -0.1042 | -0.0677 | -0.0287 | 0.0085 | -0.1534 | -0.2192 | -0.2941 | -0.3902 | -0.5469 | -0.2395 |
| 7 | -0.1094 | -0.0760 | -0.0391 | -0.0004 | 0.0349 | -0.0689 | -0.2121 | -0.2866 | -0.3731 | -0.5526 | -0.2164 |
| 8 | -0.0234 | 0.0076 | 0.0427 | 0.0774 | 0.1079 | 0.0831 | -0.0595 | -0.2104 | -0.3079 | -0.4931 | -0.1316 |
| 9 | 0.0743 | 0.1277 | 0.1921 | 0.2580 | 0.3141 | 0.1745 | 0.0998 | -0.0522 | -0.2180 | -0.3962 | -0.0071 |
| 10 | 0.3653 | 0.4176 | 0.4704 | 0.5253 | 0.5723 | 0.3990 | 0.2895 | 0.1469 | -0.0535 | -0.2865 | 0.2056 |
| 11 | 0.4786 | 0.5264 | 0.5759 | 0.6271 | 0.6718 | 0.4653 | 0.3496 | 0.2271 | 0.0864 | -0.2297 | 0.3097 |
| 12 | -0.2535 | -0.2331 | -0.2041 | -0.1613 | -0.1208 | -0.2146 | -0.2741 | -0.3430 | -0.4273 | -0.5746 | -0.3146 |
| 13 | -0.2867 | -0.2461 | -0.2030 | -0.1611 | -0.1210 | -0.2713 | -0.3264 | -0.3858 | -0.4682 | -0.6049 | -0.3447 |
| 14 | -0.2870 | -0.2456 | -0.2034 | -0.1612 | -0.1211 | -0.3240 | -0.3707 | -0.4295 | -0.5059 | -0.6328 | -0.3694 |
| 15 | -0.2858 | -0.2456 | -0.2033 | -0.1616 | -0.1217 | -0.3683 | -0.4162 | -0.4715 | -0.5422 | -0.6597 | -0.3927 |
| 16 | -0.2866 | -0.2463 | -0.2038 | -0.1622 | -0.1236 | -0.4103 | -0.4547 | -0.5057 | -0.5721 | -0.6820 | -0.4128 |
| 17 | -0.1565 | -0.1205 | -0.0819 | -0.0461 | -0.0090 | -0.1085 | -0.3842 | -0.4223 | -0.4633 | -0.6636 | -0.2958 |
| 18 | 0.1098 | 0.1379 | 0.1648 | 0.1953 | 0.2211 | 0.3982 | 0.1045 | -0.1847 | -0.2394 | -0.4626 | -0.0208 |
| 19 | 0.3780 | 0.3949 | 0.4138 | 0.4372 | 0.4513 | 0.6153 | 0.5918 | 0.2848 | -0.0149 | -0.1753 | 0.2569 |
| أ،2 | 0.0458 | 0.0737 | 0.1041 | 0.1376 | 0.2024 | 0.1207 | 0.0523 | -0.0350 | -0.1703 | -0.3789 | -0.0269 |
| أ،3 | 0.0224 | 0.0507 | 0.0827 | 0.1366 | 0.2010 | 0.0769 | 0.0155 | -0.0733 | -0.2024 | -0.4031 | -0.0533 |
| أ،4 | -0.0006 | 0.0294 | 0.0641 | 0.1328 | 0.1986 | 0.0368 | -0.0282 | -0.1123 | -0.2357 | -0.4281 | -0.0803 |
| أ،5 | -0.0211 | 0.0088 | 0.0611 | 0.1301 | 0.2004 | -0.0070 | -0.0689 | -0.1507 | -0.2691 | -0.4532 | -0.1057 |
| أ،6 | -0.0006 | 0.0558 | 0.1220 | 0.1933 | 0.2513 | 0.0545 | -0.0721 | -0.1479 | -0.2563 | -0.4626 | -0.0792 |
| أ،7 | 0.1160 | 0.1749 | 0.2418 | 0.3000 | 0.3560 | 0.4014 | 0.1074 | -0.0990 | -0.2075 | -0.4205 | 0.0270 |
| أ،8 | 0.3800 | 0.3993 | 0.4157 | 0.4389 | 0.4621 | 0.6159 | 0.5953 | 0.2878 | -0.0164 | -0.1795 | 0.2579 |
| أ،9 | 0.6371 | 0.6455 | 0.6562 | 0.6699 | 0.6778 | 0.7732 | 0.7909 | 0.7591 | 0.4379 | 0.1070 | 0.5752 |
| أ،10 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.3874 | 1.0388 | 1.4309 |
| أ،أ | 0.6072 | 0.6561 | 0.7062 | 0.7588 | 0.8058 | 0.6277 | 0.5001 | 0.3629 | 0.2059 | -0.1511 | 0.4411 |
| 2,2 | -0.0797 | -0.0089 | 0.0697 | 0.1700 | 0.2643 | 0.0087 | -0.1576 | -0.2385 | -0.3430 | -0.5115 | -0.1430 |
| 3,3 | -0.1305 | -0.0482 | 0.0500 | 0.1502 | 0.2425 | -0.0518 | -0.2189 | -0.2946 | -0.3899 | -0.5465 | -0.1859 |
| 4,4 | -0.0225 | 0.0080 | 0.0441 | 0.1066 | 0.2027 | 0.0857 | -0.0595 | -0.2096 | -0.3070 | -0.4921 | -0.1212 |
| 5,5 | 0.3676 | 0.4201 | 0.4748 | 0.5324 | 0.5814 | 0.4012 | 0.2910 | 0.1477 | -0.0534 | -0.2863 | 0.2074 |
| 6,6 | -0.1947 | -0.0972 | 0.0043 | 0.1075 | 0.1900 | -0.2189 | -0.2775 | -0.3453 | -0.4295 | -0.5767 | -0.2426 |
| 7,7 | -0.1233 | -0.0335 | 0.0669 | 0.1569 | 0.2508 | -0.0485 | -0.3765 | -0.4361 | -0.5129 | -0.6382 | -0.2497 |
| 8,8 | 0.0720 | 0.1452 | 0.2171 | 0.3005 | 0.3753 | 0.3195 | -0.0276 | -0.3893 | -0.5170 | -0.6660 | -0.1329 |
| 9,9 | 0.1943 | 0.2506 | 0.3196 | 0.3925 | 0.4551 | 0.3996 | 0.2308 | -0.0801 | -0.2369 | -0.4624 | 0.0585 |
| 10,10 | 0.6334 | 0.6442 | 0.6549 | 0.6688 | 0.6770 | 0.7723 | 0.7907 | 0.7566 | 0.4373 | 0.1124 | 0.5745 |
| المجموع | 0.0927 | 0.1262 | 0.1628 | 0.2025 | 0.2390 | 0.1453 | 0.0585 | -0.0403 | -0.1727 | -0.3712 | -0.0058 |
الفروقات في القيمة المتوقعة (بالنسبة المئوية)
يوضح الجدول التالي النسبة المئوية للقيمة المتوقعة في لعبة ذات مجموعة أوراق واحدة مطروحًا منها لعبة ذات ثماني مجموعات أوراق.
التغير في القيم المتوقعة حسب يد اللاعب مقابل بطاقة الموزع (x100)
| لاعب | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | بارِع | المجموع |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | -0.196 | -0.383 | 1.834 | 4.02 | 2.229 | 0.05 | 0.664 | 0.361 | 0.087 | -1.52 | 0.22 |
| 6 | -0.8770 | 0.0480 | 1.5840 | 3.9030 | 2.8630 | -1.0640 | -1.5170 | -1.0490 | -1.1320 | -2.4330 | -0.7380 |
| 7 | -0.2560 | 0.5920 | 2.7210 | 5.3240 | 3.3400 | -0.0070 | -1.1090 | -0.8160 | -1.3150 | -2.3840 | -0.4720 |
| 8 | 0.6060 | 1.2300 | 3.9870 | 6.3300 | 4.1900 | 0.9040 | 0.3020 | -0.3070 | -0.5740 | -2.1370 | 0.2910 |
| 9 | 3.8080 | 6.4600 | 9.1610 | 11.7320 | 6.5770 | 2.0670 | 1.1320 | 0.0300 | 0.1480 | -1.8380 | 2.2220 |
| 10 | 6.0970 | 7.3170 | 7.8980 | 10.2270 | 5.1830 | 4.6820 | 2.4980 | 1.7530 | 0.0720 | -1.2510 | 2.6040 |
| 11 | 6.4200 | 6.5830 | 7.5650 | 9.0560 | 4.8030 | 1.3220 | -0.7900 | -0.3170 | -1.9460 | 4.4940 | 1.7050 |
| 12 | 0.1670 | 0.7540 | 1.2640 | 2.4890 | 0.1350 | -1.2760 | -1.8390 | -2.0880 | 0.9840 | -0.7830 | 0.1460 |
| 13 | -0.1260 | 0.5070 | 2.1460 | 2.6670 | 0.0210 | -1.4780 | -1.9700 | 0.9410 | 0.9190 | -0.5660 | 0.3180 |
| 14 | -0.2970 | 0.6510 | 1.9930 | 2.6980 | 0.0150 | -2.0210 | 0.9460 | 1.0330 | 1.0240 | -0.2860 | 0.5000 |
| 15 | 0.5560 | 0.7690 | 1.9570 | 2.2820 | -0.4950 | 0.9270 | 0.2900 | 0.1190 | 0.2470 | -0.7990 | 0.3400 |
| 16 | 0.0300 | 0.1700 | 1.6680 | 1.8640 | -2.1330 | 3.4380 | 2.9220 | 2.6000 | 2.3870 | 0.8060 | 1.4950 |
| 17 | -0.0300 | -0.1100 | 1.0720 | 0.1630 | -2.1630 | -1.3190 | -1.3380 | 0.6910 | 0.7130 | 0.7580 | 0.1060 |
| 18 | -0.2560 | -0.2000 | -1.0990 | 0.2950 | -1.7950 | -0.9490 | -0.8890 | -1.1420 | 1.5210 | 0.9900 | 0.2340 |
| 19 | -0.1730 | -1.7470 | -1.7360 | 0.7660 | -1.4910 | -0.5200 | -1.4980 | -2.0590 | 2.7370 | 1.6770 | 0.7460 |
| أ،2 | -0.5660 | -0.2590 | 1.3280 | 7.5340 | 4.3080 | -1.3290 | -1.3120 | 2.0900 | 2.4910 | -2.0210 | 2.1220 |
| أ،3 | -0.4090 | -0.6000 | 3.0040 | 6.7580 | 3.8040 | -1.6410 | 1.9440 | 1.3040 | 2.4300 | -1.7440 | 2.2470 |
| أ،4 | -0.9750 | -0.5720 | 2.5100 | 4.2580 | 2.0490 | -0.2980 | -0.7230 | -0.1290 | 1.3080 | -2.5210 | 1.0610 |
| أ،5 | -0.8730 | -1.0720 | 0.5650 | 1.8950 | 3.2330 | -1.6930 | -1.5280 | -1.5890 | -0.6930 | -3.6740 | -0.3690 |
| أ،6 | 1.4820 | 1.8480 | 3.2870 | 8.7240 | 1.1650 | 0.5180 | 0.7480 | 1.3090 | 1.7920 | -1.8340 | 2.0600 |
| أ،7 | 1.1920 | 1.1830 | 6.7250 | 4.8180 | 0.6310 | 1.0410 | 1.3420 | 1.1640 | 1.4890 | -2.2860 | 1.8940 |
| أ،8 | 1.5370 | 1.6390 | -0.5690 | 2.0370 | 0.4540 | -0.1320 | 1.2540 | 0.0390 | 1.5550 | -1.4310 | 1.0640 |
| أ،9 | 1.5370 | -0.3990 | -0.5560 | 1.1160 | -0.4780 | 0.0020 | -0.6060 | 0.6480 | 2.1530 | -1.2700 | 1.1970 |
| أ،10 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 2.0730 | 0.2070 | 1.3970 |
| أ،أ | 3.1200 | 3.0230 | 3.5450 | 4.8720 | 2.3070 | 0.0000 | -1.3620 | -0.2430 | 0.2140 | -0.6920 | 3.3340 |
| 2,2 | 4.4790 | 4.8510 | 5.3790 | 13.1380 | 7.3480 | 0.4980 | 1.6370 | 1.6100 | 0.7540 | -1.3140 | 2.8470 |
| 3,3 | 2.2320 | 2.7290 | 11.0750 | 15.4710 | 9.7010 | 0.7020 | -0.4300 | -1.5380 | -0.8700 | -2.4920 | 2.1250 |
| 4,4 | 0.8840 | 1.8800 | 9.1320 | 16.1400 | 9.5290 | 2.4760 | 0.4550 | 0.3380 | 0.0090 | -1.4460 | 2.2100 |
| 5,5 | 7.6550 | 8.7410 | 11.2230 | 16.0940 | 12.6990 | 6.5150 | 3.1720 | 2.6130 | 0.2380 | -1.1510 | 3.7020 |
| 6,6 | 9.8410 | 11.0360 | 14.1250 | 17.1060 | 0.9170 | 2.5610 | -4.4720 | -4.0910 | -0.7110 | -2.2180 | 1.8060 |
| 7,7 | 6.8730 | 8.2850 | 12.1030 | 6.7540 | -1.1240 | -0.3840 | -0.3830 | -3.8370 | -4.2660 | -4.0800 | -0.1170 |
| 8,8 | 4.4530 | 4.2080 | 0.7370 | 2.8160 | -2.4470 | -1.5490 | -3.2240 | -1.2460 | 2.4110 | 2.7050 | 1.0500 |
| 9,9 | 1.0910 | -3.5070 | -1.2560 | 1.3820 | -4.7120 | 0.1480 | -2.4060 | -1.8530 | 3.2860 | 1.0450 | 0.8060 |
| 10,10 | -1.1490 | -1.1970 | -1.4750 | 0.2960 | -0.8740 | -0.7630 | -0.7510 | -1.2620 | 1.6580 | 2.5910 | 0.5780 |
| المجموع | 0.9370 | 1.2510 | 2.3110 | 3.6590 | 0.8050 | 0.1970 | -0.3390 | -0.3210 | 0.1480 | -1.7900 | 0.5620 |
قراءات إضافية
يقدم كتاب "نظرية البلاك جاك" لبيتر غريفين أفضل معالجة لموضوع هذه المقالة. يتناول الموضوع في الفصل الثامن، بعنوان "مجموعات أوراق متعددة وقواعد مختلفة"، والذي يستخدم مجموعة قواعد أساسية مختلفة ويحسب الفرق بين مجموعة أوراق واحدة وعدد لا نهائي من المجموعات. لا يُعطي غريفين دائمًا أرقامًا دقيقة لكل شيء، ولكنه يُعيد صياغة توزيع نسبة الفرق البالغة 0.69% بناءً على افتراضاته كما يلي:
- مضاعفة: ما يقرب من نصف 0.69٪
- لاعب بلاك جاك: 0.07%
- التقسيم: أكثر من تعويض عن فائدة لعبة البلاك جاك
- الوقوف على 12 إلى 16: "من المفترض أن التناقض المتبقي."
يواصل جريفين سرد فوائد تغييرات القواعد المختلفة في كل من المجموعة الواحدة والمجموعات غير المحدودة.
الشكر والتقدير
وأود أن أشكر دون شليزنجر على نصيحته الحكيمة بشأن تحليل وتدقيق هذه المقالة.


