برامج الألعاب التلفزيونية - التعليمات
ليس الأمر مقامرةً تمامًا، لكنني تساءلتُ دائمًا في برنامج "السعر مناسب" عن أفضل استراتيجية عند تدوير العجلة الكبيرة عندما لا تكون آخر من يدور. بافتراض عدم قدرتك على التحكم في دورانك (نتيجة عشوائية تمامًا)، مع زيادات قدرها 5 سنتات من 0.05 دولار إلى 1.00 دولار، ستحصل على دورة واحدة أو دورتين معًا، ولا يمكنك تجاوز 1.00 دولار. ما هو المبلغ الذي يجب ألا تلجأ إليه للدوران الثاني حتى تكون لديك أفضل فرصة للفوز على اللاعب الذي يدور بعدك؟
يجب على اللاعب الأول أن يدور مرة أخرى إذا كانت قيمة دورانه الأول 65 سنتًا أو أقل.
إذا كانت أي من الشروط التالية صحيحة، فيجب على اللاعب الثاني أن يدور مرة أخرى.
- نتيجته أقل من نتيجة اللاعب الأول.
- نتيجته 50 سنتًا أو أقل.
- نتيجته هي 65 سنتًا أو أقل وقد تعادل مع اللاعب الأول.
ما هي الاستراتيجية المثلى للعبة بلينكو على السعر الصحيح؟
من اليسار إلى اليمين، الجوائز هي 100 دولار، 500 دولار، 1000 دولار، 0 دولار، 10000 دولار، 0 دولار، 1000 دولار، 500 دولار، 100 دولار. أحتاج إلى معرفة التكوين الدقيق للأوتاد على اللوحة لإجراء تحليل مثالي، ولكن بمجرد النظر إلى اللوحة (انظر الرابط أعلاه)، أشعر بقوة أنه يجب على اللاعب إسقاط القرص مباشرة فوق جائزة 10000 دولار. على الرغم من أنها محاطة بصفرين، فإن جميع الجوائز الأخرى باهتة مقارنة بالجائزة الكبرى. لذا يجب أن تكون استراتيجية اللاعب هي زيادة احتمالية الجائزة الكبرى عن طريق إسقاطها مباشرة فوقها. لتأكيد أو دحض فرضيتي، أجريت بحثًا وهناك الكثير من الروابط المخصصة لدراسة هذه اللعبة. هذا ( www.amstat.org/publications/jse/v9n3/biesterfeld.html ) هو أحد أفضل الروابط، وهو ما يتفق مع استنتاجي. يذكر جزئيًا أن القيمة المتوقعة لإسقاط القرص في المنتصف هي 2557.91 دولارًا، وعلى جانبي المنتصف هي 2265.92 دولارًا، وتتناقص تدريجيًا كلما ابتعدت عن المركز.
في برنامج المسابقات "لنعقد صفقة"، هناك ثلاثة أبواب. على سبيل المثال، لنفترض أن بابين يكشفان عن ماعز، وواحد يكشف عن سيارة جديدة. يختار مقدم البرنامج، مونتي هول، متسابقين لاختيار باب. في كل مرة يفتح مونتي بابًا يكشف عن ماعز أولاً. لنفترض هذه المرة أنه يخص المتسابق الأول. مع أن مونتي لم يفعل ذلك، ماذا لو عرض مونتي على المتسابق الآخر فرصة تغيير الباب في هذه المرحلة، إلى الباب الآخر غير المفتوح. هل يجب عليه تغيير الباب؟
نعم! يكمن سر هذه المشكلة في أن المُضيف مُقدّرٌ له أن يفتح بابًا فيه عنزة. إنه يعرف أي باب فيه السيارة، لذا بغض النظر عن الأبواب التي يختارها اللاعبون، يمكنه دائمًا الكشف عن عنزة أولًا. يُعرف هذا السؤال باسم "مفارقة مونتي هول". يعود جزء كبير من الالتباس حوله إلى أنه غالبًا ما يُساء تفسير السؤال عند صياغته، حيث يُغفل المُضيف معرفة مكان السيارة، ويكشف دائمًا عن عنزة أولًا. أعتقد أن بعض اللوم يقع على مارلين فوس سافانت ، التي أساءت صياغة السؤال في عمودها. لنفترض أن الجائزة خلف الباب رقم 1. فيما يلي ما سيحدث إذا اتبع اللاعب (المتسابق الثاني) استراتيجية عدم التبديل.
- يختار اللاعب الباب 1 --> يفوز اللاعب
- يختار اللاعب الباب 2 --> يخسر اللاعب
- يختار اللاعب الباب رقم 3 --> ويخسر اللاعب
فيما يلي ما قد يحدث إذا كان لدى اللاعب استراتيجية للتبديل.
- يختار اللاعب الباب 1 --> يكشف المضيف عن الماعز خلف الباب 2 أو 3 --> ينتقل اللاعب إلى باب آخر --> يخسر اللاعب
- يختار اللاعب الباب 2 --> يكشف المضيف عن الماعز خلف الباب 3 --> ينتقل اللاعب إلى الباب 1 --> يفوز اللاعب
- يختار اللاعب الباب 3 --> يكشف المضيف عن الماعز خلف الباب 2 --> ينتقل اللاعب إلى الباب 1 --> يفوز اللاعب
لذا، بعدم تغيير اللاعب، تكون فرص فوزه 1/3. أما بتغييره، فتصبح فرص فوزه 2/3. لذا، يجب على اللاعب تغييره بالتأكيد.
لمزيد من القراءة عن مفارقة مونتي هول، أنصحك بقراءة المقال على ويكيبيديا .
سؤالي يتعلق بمشكلة تُعرف باسم "مفارقة المظروفين". أنت في برنامج ألعاب، وأمامك مظروفان، يحتوي كل منهما على مبلغ غير معروف من المال. قيل لك إن أحد المظروفين يحتوي على ضعف المبلغ الموجود في الآخر. طُلب منك الآن اختيار مظروف. اخترت أحدهما، وكان يحتوي على 50,000 دولار. قيل لك الآن إنه يمكنك الاحتفاظ بالمظروف الذي اخترته، أو استبداله بالمظروف الآخر. هل يجب عليك استبداله؟ إذا كنت تعلم مسبقًا أنه يمكنك استبداله، فلن يكون هناك فرق، لأنك ستختار المظروف الذي تريده في النهاية. ولكن بما أنك لا تعرف عن الاستبدال إلا بعد اختيار المظروف، فإن الاختيار الأصلي وخيار الاستبدال هما حدثان مستقلان، أليس كذلك؟ مع ذلك، عند اتخاذ قرار الاستبدال من عدمه، يحتوي المظروف الآخر إما على ضعف المبلغ الحالي أو نصفه. أي أنه يحتوي إما على 100 ألف دولار أو 25 ألف دولار. بما أن احتمال حدوث أي منهما 50%، فإن القيمة المتوقعة للمظروف الآخر هي 62,500 دولار. بشكل عام، إذا افترضنا أن x = المبلغ الذي اخترته أصلاً، فإن القيمة المتوقعة للظرف الآخر هي ١٫٢٥x. لذلك، من الصحيح دائمًا التبديل. هل هذا صحيح؟ شكرًا لك.
أنا مُلِمٌّ بهذه المسألة. أتناولها في موقعي الإلكتروني لمسائل الرياضيات ، المسألة رقم 6. هناك، أتناول الحالة العامة، بما في ذلك عدم النظر في الظرف الأول إطلاقًا. مع ذلك، للإجابة على سؤالك، لا يُمكننا تجاهل مكان إقامة اللعبة. ذكرتَ أنها كانت "برنامج مسابقات". في معظم برامج المسابقات، يُعدّ مبلغ 50,000 دولار فوزًا رائعًا. نادرًا ما يصل مُتسابقو برنامج "السعر الصحيح" إلى هذا المبلغ. أعتقد أن أقل من 50% من مُتسابقي برنامج "من سيربح المليون" يصلون إلى هذا المبلغ. في الوقت نفسه، يُعدّ الفوز بمبلغ 25,000 دولار أمرًا شائعًا في برامج المسابقات. عادةً ما تُربح السيارات في برنامج "السعر الصحيح"، والتي تبلغ قيمتها حوالي 25,000 دولار. يُعدّ الفوز بمبلغ 32,000 دولار فوزًا شائعًا في برنامج "من سيربح المليون". يبلغ مُتوسط الفوز في برنامج "جيوباردي" لكل حلقة حوالي 25,000 دولار. حقق كين جينينغز العظيم مُتوسط 34,091 دولارًا فقط خلال 74 فوزًا. إذن، ما أقصده هو أن 50,000 دولار فوزٌ رائعٌ في برنامج المسابقات، وجوائز 100,000 دولار أقل شيوعًا بكثير من 25,000 دولار. لذا، بصفتي خبيرًا في برامج المسابقات، أرى أن احتمالية وجود 25,000 دولار في الظرف الآخر أكبر من 100,000 دولار. لذا، أقول في مثالكم إنه من الأفضل الاحتفاظ بـ 50,000 دولار. كما يُظهر هذا أنه لا يُمكن أبدًا افتراض أن احتمالية وجود نصف أو ضعف المبلغ في الظرف الآخر هي 50/50 تمامًا. بمجرد معرفة المبلغ ووضعه في سياق مكان العرض، يُمكنك اتخاذ قرار ذكي بشأن التغيير، مما يُلغي حجة 1.25x.
سؤالي يتعلق ببرنامج المسابقات "صفقة أو لا صفقة"، وهو برنامج مشهور جدًا في أستراليا وسيُعرض قريبًا في إنجلترا. يُعرض على المتسابق ست وعشرون حقيبة مرقمة، تحتوي كل منها على مبلغ مالي مخفي، يتراوح بين 50 سنتًا و200 ألف دولار أمريكي، كما هو موضح أدناه.
- 0.50 دولارًا
- 1 دولار
- 2 دولار
- 5 دولارات
- 10 دولارات
- 25 دولارًا
- 50 دولارًا
- 75 دولارًا
- 100 دولار
- 150 دولارًا
- 250 دولارًا
- 500 دولار
- 750 دولارًا
- 1000 دولار
- 1500 دولار
- 2000 دولار
- 3000 دولار
- 5000 دولار
- 7,500 دولار
- 10,000 دولار
- 15000 دولار
- 30,000 دولار
- 50,000 دولار
- 75,000 دولار
- 100,000 دولار
- 200,000 دولار
يختار المتسابق إحدى الحقائب لتكون حقيبته. ومن خلال عملية إقصاء، بفتح الحقائب الأخرى، يحاول معرفة مقدار المال الذي يملكه، أو ما إذا كان من الحكمة قبول "عرض البنك". تعتمد عروض البنك على المتوسط الحسابي للحقائب المتبقية، ولكنها لا تعادله. لذا، إذا كانت معظم الحقائب الكبيرة المتبقية، فهناك احتمال كبير أن تكون حقيبة المتسابق قيّمة، وبالتالي سيكون عرض البنك سخيًا. على العكس، إذا كان اللاعب أقل حظًا وفتح الحقائب الأكثر قيمة، فسيكون عرض البنك منخفضًا. ما هي أفضل استراتيجية يمكن اتباعها إذا كنت متسابقًا في هذه اللعبة؟ تتمثل الاستراتيجية غير الرياضية في تجاهل عروض البنك والاستمرار في فتح الحقائب حتى يتم فتح 200,000 دولار واستبعادها، أو فتح 100,000 دولار و75,000 دولار واستبعادهما. ما هي الرياضيات وراء هذه اللعبة، يا Wizard؟
انطلقت مسابقة "صفقة أم لا" هنا في الولايات المتحدة. قواعدها متشابهة، إلا أن جوائزنا تصل إلى مليون دولار كما يلي.
- 0.01
- 1
- 5
- 10
- 25
- 50
- 75
- 100
- 200
- 300
- 400
- 500
- 750
- 1000
- 5000
- 10000
- 25000
- 50000
- 75000
- 100000
- 200000
- 300000
- 400000
- 500000
- 750000
- 1000000
وهنا تدفق اللعبة:
- يختار اللاعب حالة واحدة لنفسه
- يفتح اللاعب ستة من الحالات الـ 25 المتبقية.
- يقدم المصرفي عرضًا.
- إذا رفض اللاعب فإنه يفتح خمسة صناديق أخرى من أصل 19 صندوقًا متبقية.
- يقدم المصرفي عرضًا.
- إذا رفض اللاعب فإنه يفتح أربعة صناديق أخرى من أصل 14 صندوقًا متبقيًا.
- يقدم المصرفي عرضًا.
- إذا رفض اللاعب فإنه يفتح ثلاثة صناديق أخرى من أصل 10 صناديق متبقية.
- يقدم المصرفي عرضًا.
- إذا رفض اللاعب فإنه يفتح حالتين أخريين من الحالات السبع المتبقية.
- يقدم المصرفي عرضًا.
- إذا رفض اللاعب فإنه يفتح حالة أخرى من الحالات المتبقية.
- استمر في تكرار الخطوتين 11 و12 حتى يقبل اللاعب العرض أو يكون لديه آخر حالة غير مفتوحة.
يوضح الرسم البياني التالي القيمة المتوقعة للاعب والعرض الذي قدمه المصرفي.
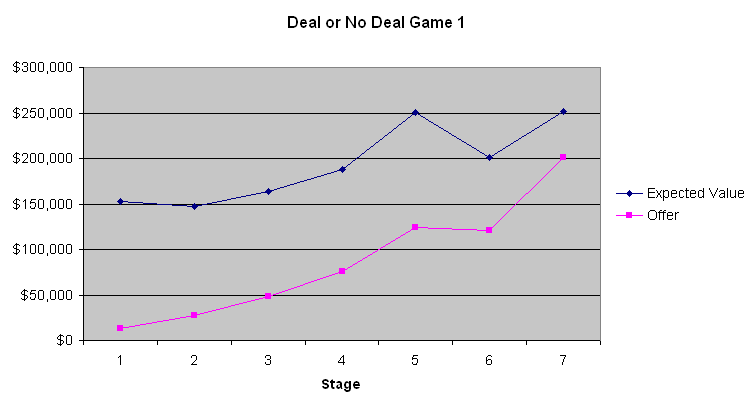
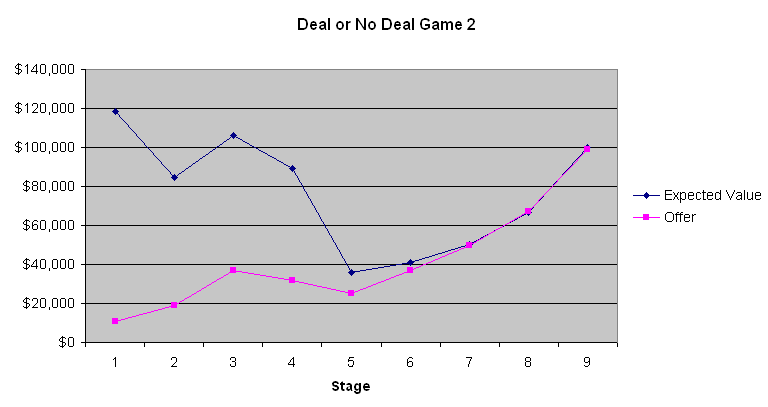
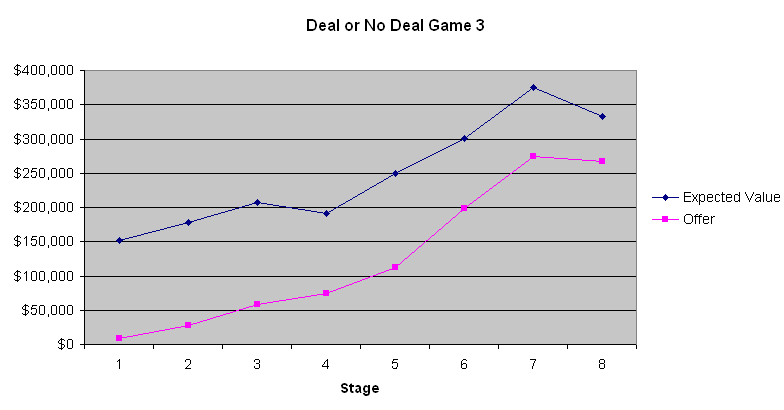
أوضح ما يمكن تعلمه من هذه الرسوم البيانية الثلاثة هو أن أول أربعة إلى ستة عروض مصرفية هي صفقات سيئة. تحتوي الحقيبة المتوسطة على 131،477.54 دولارًا قبل فتح أي منها. إن تقديم 9000 إلى 13000 دولار فقط في المرحلة الأولى هو صفقة لا يقبلها إلا الأحمق. ومع ذلك، تتحسن العروض تدريجيًا. تُظهر لنا اللعبة 2 أن القيم المتوقعة كانت تقريبًا هي نفسها التي يقدمها المصرفي في نهاية اللعبة عندما كانت القيمة المتوقعة للاعب منخفضة نسبيًا. ومع ذلك، في اللعبتين 1 و3 عندما كانت القيم المتوقعة أعلى، كان المصرفي على ما يبدو يحاول الاستفادة من طبيعة معظم الناس الذين يتجنبون المخاطرة عند المشاركة بمبالغ كبيرة. لا أعرف ما إذا كان ذلك مهمًا، لكن المتسابق في اللعبة 2 بدا وكأنه مقامر يريد الفوز الكبير. بناءً على تعليقات المضيف، الذي يتواصل مع المصرفي عبر الهاتف، يبدو أن المصرفي يأخذ أقوال المتسابقين وأفعالهم في الاعتبار. لو كنت مكان المصرفي، لتصرفت بنفس الطريقة إلى حد كبير.
إذا لم يكن اللاعب يخشى المخاطرة ولا يميل إليها، ويتجاهل أيضًا التبعات الضريبية، فعليه الاستمرار في رفض عروض المصرفي حتى يتجاوز عرضه متوسط الحقائب المتبقية. بالنسبة لمعظم الناس، تُفضّل الطبيعة التصاعدية لقانون ضريبة الدخل قبول الصفقة. وكما ذكرتُ سابقًا، أود أن أقول تقريبًا إن قيمة المال تتناسب طرديًا مع لوغاريتم المبلغ. لذا، كلما زادت ثروتك عند بدء اللعبة، زاد ميلك للمقامرة ورفض عروض المصرفي. مع هذه المبالغ الضخمة، لا توجد استراتيجية تناسب الجميع. مع ذلك، يمكنني القول بثقة تامة إنه يجب على اللاعب رفض أول أربعة إلى ستة عروض، ثم قبول العروض الأخرى كل حالة على حدة (مع مراعاة التورية).
الروابط:
يمكنك مشاهدة Deal or No Deal على NBC.com.
أرشيف العروض السابقة.
أشاهد برنامج "صفقة أو لا صفقة". أدركتُ أن "العرض" من المصرفي هو مجرد القيم المتبقية للصناديق مقسومة على عدد الصناديق (تقريبًا). هل هناك أي استراتيجية لهذه اللعبة، أم أن "الصفقة" دائمًا ما تكون مقبولة؟ هل يعتمد الأمر على عدد الصناديق التي يجب فتحها أم ماذا؟
كما يُظهر عمودي بتاريخ ٢٦ ديسمبر ٢٠٠٥، عادةً ما يكون عرض المُصرفي أقل بكثير من متوسط الحالات المتبقية. مع ذلك، لو كان الأمر كذلك دائمًا، لكانت جميع الاستراتيجيات تحمل القيمة المتوقعة نفسها. سيُبدي اللاعب عدم اكتراثه بكل عرض.
في بداية "الصفقة أو عدم الصفقة"، فإن احتمالات اختيار حالة المليون دولار هي 1 من 26. بعد استبعاد جميع الحالات باستثناء 1، ما هي احتمالات أن تحتوي حالتي على مليون دولار. هل هي 50-50 أم لا تزال 1 من 26؟
50-50
في مقالك بتاريخ 5 أبريل/نيسان 2006، ذكرتَ أنه إذا لم يتبقَّ سوى حالتين في "صفقة أو لا صفقة" وكان المليون دولار لا يزال قائمًا، فإن احتمال حصول حالتي على المليون هو 50/50. لا أتفق معك. أليس هذا مجرد شكل مختلف من مشكلة مونتي هول؟ أي أن احتمال وجود المليون دولار على المسرح أكبر من احتمال وجوده في حالته؟
لا، أجد الكثير من الناس يتجادلون معي حول هذا الموضوع. يدّعي العديد من الكُتّاب أن الاحتمالات لا تتغير عند إضافة معلومات إضافية. لذا، إذا بدأ الاحتمال من ١ إلى ٢٦، فيجب أن يبقى عند هذا الحد. على عكس ما يقوله بائعو أنظمة المراهنات، فإن الاحتمالات قابلة للتغيير بالفعل عند إضافة معلومات إضافية. لا أريد أن أحاول تدريس أساسيات الاحتمالات هنا، ولكن أي كتاب رياضيات جامعي يتناول الاحتمال الشرطي أو نظرية بايز ينبغي أن يغطي هذا الموضوع بشكل جيد.
دعني أشرح ما حدث في برنامج "لنعقد صفقة". سيختار المتسابق ستارة واحدة من ثلاث ستائر. تحتوي إحداها على جائزة قيّمة للغاية والأخرى على جائزتين أصغر. من أجل المناقشة، دعنا نقول أن خلف إحدى الستائر سيارة وخلف الستارتين الأخريين عنزة. ثم سيفتح مونتي دائمًا، وأكرر دائمًا، إحدى الستارتين غير المختارتين ليكشف عن عنزة. بعد مئات العروض، يعني هذا أن مونتي هول (المضيف) كان يعرف مكان السيارة وفتح عمدًا ستارة كشفت عن عنزة. من الواضح أنه عندما اختار اللاعب ستارته، كان احتمال احتوائها على السيارة 1/3 واحتمال احتوائها على السيارة في إحدى الستارتين غير المختارتين هو 2/3. ثم يكون مونتي مقدرًا له أن يفتح ستارة غير مختار تحتوي على هدف. مقدر هي الكلمة الأساسية هنا. نظرًا لأن مونتي لا يستطيع فتح ستارة اللاعب في هذه المرحلة، فإن احتمالية كشف ستارة اللاعب عن السيارة تبقى عند 1/3. يبقى احتمال ظهور السيارة في ستارة غير مفتوحة عند ٢/٣، مع أن جميعها الآن على ستارة واحدة. لذا، بعد ظهور الماعز، يكون احتمال ظهور السيارة في ستارة اللاعب ١/٣، واحتمال ظهور السيارة في الستارة الأخرى غير المفتوحة ٢/٣، مما يجعل التبديل خيارًا حكيمًا.
يوضح الجدول التالي جميع النتائج المحتملة. في حالة اختيار اللاعب الستارة بالسيارة، كان على مونتي فتح الستارة عشوائيًا. كما ترى، فإن عدم التبديل يؤدي إلى احتمال فوز بنسبة 1/3، بينما يؤدي التبديل إلى احتمال فوز بنسبة 2/3.
دعونا نعقد صفقة
| لاعب يختار | سيارة | ستارة مفتوح | احتمال | الفوز بـ التبديل |
| 1 | 1 | 1 | 0% | غير متوفر |
| 1 | 1 | 2 | 5.56% | ن |
| 1 | 1 | 3 | 5.56% | ن |
| 1 | 2 | 1 | 0% | غير متوفر |
| 1 | 2 | 2 | 0% | غير متوفر |
| 1 | 2 | 3 | 11.11% | ي |
| 1 | 3 | 1 | 0% | غير متوفر |
| 1 | 3 | 2 | 11.11% | ي |
| 1 | 3 | 3 | 0% | غير متوفر |
| 2 | 1 | 1 | 0% | غير متوفر |
| 2 | 1 | 2 | 0% | غير متوفر |
| 2 | 1 | 3 | 11.11% | ي |
| 2 | 2 | 1 | 5.56% | ن |
| 2 | 2 | 2 | 0% | غير متوفر |
| 2 | 2 | 3 | 5.56% | ن |
| 2 | 3 | 1 | 11.11% | ي |
| 2 | 3 | 2 | 0% | غير متوفر |
| 2 | 3 | 3 | 0% | غير متوفر |
| 3 | 1 | 1 | 0% | غير متوفر |
| 3 | 1 | 2 | 11.11% | ي |
| 3 | 1 | 3 | 0% | غير متوفر |
| 3 | 2 | 1 | 11.11% | ي |
| 3 | 2 | 2 | 0% | غير متوفر |
| 3 | 2 | 3 | 0% | غير متوفر |
| 3 | 3 | 1 | 5.56% | ن |
| 3 | 3 | 2 | 5.56% | ن |
| 3 | 3 | 3 | 0% | غير متوفر |
في لعبة "صفقة أم لا صفقة"، لا شيء مُقدّر. لنفترض أن المبالغ المتبقية في "صفقة أم لا صفقة" هي 0.01 دولار، ودولار واحد، ومليون دولار. مع بقاء ثلاث أوراق، من الممكن أن تحتوي الورقة المفتوحة على مليون دولار. يوضح الجدول التالي النتائج المحتملة مع بقاء ثلاث أوراق. تذكر، لا يمكن للاعب فتح ورقته الخاصة.
صفقة أو لا صفقة
| لاعب يختار | مليون دولار | قضية مفتوح | احتمال | الفوز بـ التبديل |
| 1 | 1 | 1 | 0% | غير متوفر |
| 1 | 1 | 2 | 5.56% | ن |
| 1 | 1 | 3 | 5.56% | ن |
| 1 | 2 | 1 | 0% | غير متوفر |
| 1 | 2 | 2 | 5.56% | يائس |
| 1 | 2 | 3 | 5.56% | ي |
| 1 | 3 | 1 | 0% | غير متوفر |
| 1 | 3 | 2 | 5.56% | ي |
| 1 | 3 | 3 | 5.56% | يائس |
| 2 | 1 | 1 | 5.56% | يائس |
| 2 | 1 | 2 | 0% | غير متوفر |
| 2 | 1 | 3 | 5.56% | ي |
| 2 | 2 | 1 | 5.56% | ن |
| 2 | 2 | 2 | 0% | غير متوفر |
| 2 | 2 | 3 | 5.56% | ن |
| 2 | 3 | 1 | 5.56% | ي |
| 2 | 3 | 2 | 0% | غير متوفر |
| 2 | 3 | 3 | 5.56% | يائس |
| 3 | 1 | 1 | 5.56% | يائس |
| 3 | 1 | 2 | 5.56% | ي |
| 3 | 1 | 3 | 0% | غير متوفر |
| 3 | 2 | 1 | 5.56% | ي |
| 3 | 2 | 2 | 5.56% | يائس |
| 3 | 2 | 3 | 0% | غير متوفر |
| 3 | 3 | 1 | 5.56% | ن |
| 3 | 3 | 2 | 5.56% | ن |
| 3 | 3 | 3 | 0% | غير متوفر |
يُظهر جدول "الصفقة أم لا" أنه مع بقاء ثلاث حالات، يكون احتمال فتح اللاعب لحقيبة المليون دولار 1/3 (أي احتمال ضعيف للفوز)، واحتمال فوز اللاعب الذي يغير أوراقه 1/3، واحتمال خسارته 1/3. وبالتالي، تكون الاحتمالات متساوية عند تغيير الأوراق. إذا تبقى حالتان فقط، يكون احتمال حصول كل حالة على الجائزة الأكبر 50/50.
حان وقت سؤال آخر حول "صفقة أم لا". لنفترض، بعد كل الصفقات التي أجراها المصرفي وظهور سيلين ديون كضيفة شرف، أن يتبقى لديك حقيبتان، إحداهما بقيمة 500,000 دولار والأخرى بقيمة مليون دولار. أفترض أن عرض المصرفي سيكون أقل بقليل من 750,000 دولار. أيهما ستختار؟ ماذا لو كانت الحقيبتان المتبقيتان هما الحقيبتان اللتان تبلغ قيمتهما 0.01 دولار والأخرى بقيمة مليون دولار؟ أعتقد أن الأمر كله يتعلق بكونك مقامرًا أم لا، ولا علاقة له بالاحتمالات. سبب سؤالي هو أنني أتساءل إن كان أي شخص سيفوز بمليون دولار (حتى لو اختار الحقيبة السحرية).
عندما تصبح الجوائز مبالغ مؤثرة، ينبغي على اللاعب الحكيم أن يلعب بحذر على حساب تعظيم القيمة المتوقعة. الاستراتيجية الجيدة هي تعظيم السعادة المتوقعة. أعتقد أن دالة جيدة لقياس السعادة هي لوغاريتم إجمالي ثروتك. لنفترض أن شخصًا لديه ثروة حالية قدرها 100,000 دولار، وعُرضت عليه حالتان: 0.01 دولار و1,000,000 دولار. بقبول "عدم وجود صفقة"، تكون السعادة المتوقعة 0.5 * لوغاريتم ($100,000.01) + 0.5 * لوغاريتم ($1,100,000) = 5.520696. ليكن b هو عرض البنك الذي لا يمانع اللاعب في قبوله.
log(b) = 5.520696
ب = 10 5.520696
ب = 331,662.50 دولارًا.
لذا، يجب أن يكون هذا اللاعب الافتراضي غير مبالٍ بعرض البنك البالغ 331,662.50 دولارًا. كلما قلّت ثروتك عند بدء اللعبة، كان عليك اللعب بتحفظ أكبر. عادةً ما تكون عروض البنك في المراحل الأخيرة من اللعبة قريبة من القيمة المتوقعة، وأحيانًا أكثر بقليل. الحالة المنطقية الوحيدة التي يمكن أن يفوز فيها اللاعب بالمليون هي إذا كان لديه ثروة كبيرة عند بدء اللعبة و/أو كانت عروض البنك بخيلة بشكل غير عادي. يبدو أن المنتجين يفضلون أفراد الطبقة المتوسطة المجتهدين، لذلك من غير المرجح أن نرى شخصًا يستطيع تحمل التهاون عندما يتعلق الأمر بمبالغ كبيرة. كما أنني لم أرَ البنك يقدم عروضًا أقل من 90٪ من القيمة المتوقعة في وقت متأخر من اللعبة. الوقت الذي سنرى فيه شخصًا يفوز بالمليون هو عندما يظهر مقامر منحط في العرض ولا يمكنه التوقف. عندما يحدث ذلك، سأكون مشجعًا للمصرفي.
هذا متابعة لبرنامج "صفقة أو لا صفقة"، الذي شاهدته لأول مرة مؤخرًا. يفترض تحليلك أن الكازينو لا يعرف قيمة المال في الحقيبة. مع ذلك، في البرنامج الذي شاهدته، في المرحلة النهائية، اختار كلا المتسابقين حقيبة قيّمة، وعُرضت عليهما (أو كانا سيُعرضان عليهما، إذ انسحب أحدهما بالفعل) صفقات أعلى من القيمة المتوقعة (EV). في الحالة الأكثر تطرفًا، كان سيُعرض على لاعب 687 ألف دولار بينما المبلغان المتبقيان هما 500 ألف دولار و750 ألف دولار. التفسير المنطقي الوحيد لذلك هو أن المصرفي يعرف قيمة حقيبة اللاعب، والصفقات المعروضة مبنية على ذلك.
هذه مجرد وجهة نظري الشخصية، ولا داعي للرد.
شكرًا لعدم توقعك ردًا، ولكني عادةً ما أرد على أسئلة برامج المسابقات. يدّعون في كل حلقة أن المبالغ في الحالات توضع عشوائيًا، وأن لا هاوي ولا المصرفي يعرفان النتائج. لم يُدّعى هذا مطلقًا في برنامج "دعونا نعقد صفقة"، حيث كان مونتي هول يعلم بوضوح. لقد رأيتُ أيضًا المصرفي يعرض قيمة أكبر من المتوقع كعرض أخير، خاصةً عندما يتعلق الأمر بمبالغ كبيرة. برأيي الراسخ، هذا ليس لأن المصرفي يعرف ما بداخل حالة اللاعب. في الخمسينيات من القرن الماضي، كانت هناك فضيحة ضخمة عندما عُرف أن برنامج "21" وغيره قد تم التلاعب بنتائجه. لا يوجد سبب مقنع لتدمير برنامج ناجح، ونزاهة جميع برامج المسابقات، من خلال اختلاس بعض أموال الجوائز من خلال عروض البنك.
أستطيع أن أقدم ثلاث نظريات تفسر لماذا يقدم المصرفي في بعض الأحيان مبلغا أكبر من المتوسط في الحالات المتبقية.
- يحاول المسلسل تصوير المصرفي وهو يُبذّر المال في مكتبه. غالبًا ما يُعلّق هاوي ماندل على مزاج المصرفي ونبرة صوته. ربما يُضفي تصوير المصرفي كمحاسبٍ يتجنب المخاطرة، مُفضّلًا تقليل خسائره على المخاطرة بتقديم جائزة كبيرة، طابعًا أكثر دراماتيكية.
- المصرفي الحقيقي يتجنب المخاطرة. هذا خارج نطاق تخصصي، ولكن حسب فهمي، عادةً ما تُنتج برامج المسابقات وبرامج الواقع شركات مستقلة عن شبكة التلفزيون. ستسعى هذه الشركات الصغيرة إلى الاستعانة بشركة تأمين لتقليل خطر فوز المتسابقين بالجوائز الكبرى. في هذه الحالة، ستكون شركة التأمين هي المصرفي الحقيقي، وقد تؤثر على سلوك المصرفي في البرنامج. شركات التأمين التي تُؤمّن على أشياء غريبة كهذه ليست شركات عملاقة، وقد تُفضّل المجازفة عند وجود مبالغ كبيرة.
في مثالكم، كان عرض البنكي أعلى من القيمة المتوقعة بنسبة 9.92%. لو كان البنكي يتبع معيار كيلي ، لكان هذا العرض قد قُدّم برأس مال إجمالي قدره 782,008 دولارات فقط، وهو أقل من الحد الأقصى للجائزة. لا يمكن لأي شركة تأمين تحترم نفسها أن تكون متحفظة إلى هذا الحد. من الواضح أن هذا السبب وحده لا يبرر العرض المذكور في مثالكم.
- يحاول البرنامج تصوير المتسابقين بمظهر الغباء والجشع. برامج مثل "هل أنت أذكى من طالب الصف الخامس" وبرنامج "المشي في الشارع" على برنامج "ذا تونايت شو" ما كانت لتنجح لو لم نجد متعة في الضحك على من يعجزون عن فهم المعلومات العامة. أما برنامجا "صديق أم عدو" و "الحلقة الأضعف" فقد كانا رائعين في كشف الجشع في الطبيعة البشرية. لا بد لي من الاعتراف بأنني أشعر بشعور من الشماتة عندما يرفض أحد المتسابقين عرضًا أعلى من المتوقع، ويقبل بأقل عرض.
أعتقد أن السبب هو مزيج من هذه الأسباب الثلاثة، ولكن السبب الثالث هو السبب الرئيسي.
لو أنهيت إجابتي هنا، لوجدتُ بالتأكيد تعليقاتٍ تتساءل عمّا إذا كانت عروض المصرفي الافتراضية ستُقدّم بالفعل. وهذا يعني ضمناً أنها مُضخّمةٌ لإحداث تأثيرٍ دراماتيكي. لقد سجّلتُ تفاصيل 13 لعبة. في إحداها، مع ثلاث حالات متبقية (1000 دولار، 5000 دولار، و50000 دولار)، كان المتوسط 18667 دولارًا، وكان العرض 21000 دولار. أي بزيادة 12.5% عن القيمة المتوقعة. في لعبة أخرى، مع حالتين متبقيتين (400 دولار و750000 دولار)، كان المتوسط 375200 دولارًا، وكان العرض 400000 دولار. أي بزيادة 6.6% عن القيمة المتوقعة. لذا، لا أرى أي سببٍ للتشكيك في نزاهة العروض الافتراضية.
الروابط:
صيغة الصفقة أو عدم الصفقة : تعرض هذه الصفحة الصيغ القديمة والجديدة لحساب عرض المصرفي، استنادًا إلى اللعبة المجانية على موقع الويب Deal or No Deal.
ما هو المبلغ الذي ستراهن به، في حذاء كل شخص، في لعبة Final Jeopardy، مع هذه النتائج:
اللاعب أ: 10000 دولار
اللاعب ب: 8000 دولار
اللاعب ج: 3500 دولار
دعوني أبدأ ببعض الافتراضات. أولًا، سأفترض أن اللاعبين الثلاثة ليس لديهم أي معرفة مسبقة بسلوكيات الرهان في لعبة Final Jeopardy، باستثناء احتمالات الصواب في الجدول المعروض. ثانيًا، سأفترض أن معرفة الفئة لا تُجدي نفعًا. ثالثًا، سأفترض أيضًا أن جميع المتسابقين الثلاثة يسعون للفوز، لا لمشاركة لاعب آخر في حالة التعادل.
لنبدأ باللاعب ج. عليه أن يتوقع أن يراهن أ بمبلغ 6001 دولار أمريكي ليبقى فوق ب إذا كان ب مُصيبًا. أما إذا كان أ مُخطئًا، فسيُخفض ذلك رهانه إلى 3999 دولارًا أمريكيًا. سيحتاج ج إلى المراهنة بمبلغ 500 دولار أمريكي على الأقل، وأن يكون مُصيبًا، ليتغلب على أ في هذه الحالة. مع ذلك، برأيي، إذا كان الفوز مُلزمًا بالفوز، فمن الأفضل أن تُراهن بمبالغ كبيرة. لذا، لو كنتُ مكان اللاعب ج، لراهنتُ بكل شيء.
ب متردد بين الرهان الكبير والصغير. يجب أن يكون الرهان الصغير 999 دولارًا أو أقل، ليبقى أعلى من ج إذا كان ج صحيحًا. فائدة الرهان الصغير هي البقاء أعلى من ج مهما حدث، على أمل أن يكون أ كبيرًا ويكون مخطئًا. ليس بالضرورة أن يستمر الرهان الكبير حتى النهاية، ولكنه قد يستمر أيضًا. فائدة الرهان الكبير هي أمل أن يكون أ صغيرًا أو كبيرًا ويكون خاطئًا، لكن كلاهما يتطلب أن يكون ب صحيحًا.
يريد "أ" أساسًا أن يسير على نفس خطى "ب". يمكن أن يكون الرهان الصغير على "أ" أي مبلغ يتراوح بين 0 و1000 دولار، وسيبقى أعلى من "ب" إذا راهن "ب" بـ 999 دولارًا. يجب أن يكون الرهان الكبير 6001 دولارًا، لضمان الفوز إذا كان "أ" مُصيبًا، وللحفاظ على الأمل إذا راهن "ب" بأموال طائلة، وكان جميع اللاعبين الثلاثة مُخطئين.
للمساعدة في حساب احتمالات النتائج الثمانية المحتملة للإجابات الصحيحة والخاطئة، اطلعتُ على نتائج مسابقة "جيبردي" النهائية للمواسم من ٢٠ إلى ٢٤، من موقع j-archive.com (لم يعد متاحًا). إليكم النتائج: اللاعب أ هو المتصدر، يليه اللاعب ب، ثم ج في المركز الأخير.
النتائج المحتملة في الخطر النهائي
| اللاعب أ | اللاعب ب | اللاعب ج | احتمال |
| يمين | يمين | يمين | 21.09% |
| يمين | يمين | خطأ | 9.73% |
| يمين | خطأ | يمين | 10.27% |
| خطأ | يمين | يمين | 8.74% |
| يمين | خطأ | خطأ | 13.33% |
| خطأ | يمين | خطأ | 10.27% |
| خطأ | خطأ | يمين | 8.63% |
| خطأ | خطأ | خطأ | 17.92% |
باستخدام نوع منطق نظرية اللعبة الذي أشرحه في المسألة 192 على موقعي mathproblems.info ، أجد أن A و B يجب أن يقوما باختيار استراتيجيتهما بشكل عشوائي على النحو التالي.
يجب على اللاعب (أ) أن يراهن بمبلغ كبير باحتمالية 73.6% ومبلغ صغير باحتمالية 26.4%.
يجب على اللاعب B أن يراهن بمبلغ كبير باحتمالية 67.3% ومبلغ صغير باحتمالية 32.7%.
يجب على اللاعب C أن يراهن بمبلغ كبير مع احتمال 100.0%.
إذا تم اتباع هذه الاستراتيجية، فإن احتمال فوز كل لاعب سيكون على النحو التالي:
اللاعب أ: 66.48%
اللاعب ب: 27.27%
اللاعب ج: 6.25%
بالمناسبة، بناءً على الجدول أعلاه، احتمالية إجابة المتصدر الصحيحة في لعبة Final Jeopardy هي ٥٤.٤٪، وللثاني ٤٩.٨٪، وللثالث ٤٨.٧٪. الاحتمالية الإجمالية هي ٥١.٠٪.
كملاحظة عملية، يمتلك اللاعبون معرفةً بسلوكيات المراهنة. برأيي، يميل اللاعبون إلى المراهنة بمبالغ كبيرة أكثر مما هو مبرر رياضيًا. ومن المثير للاهتمام، أجد المراهنة في لعبة "المضاعفة اليومية" مُتحفّظة أكثر مما هو مبرر رياضيًا. أحد أسباب اعتقادي بنجاح كين جينينغز هو المراهنة العدوانية على لعبة "المضاعفة المزدوجة". على أي حال، لو كنتُ مشاركًا في البرنامج، لافترضتُ أن اللاعبين الآخرين سيراهنان بعنف. لذا، ستكون رهاناتي الفعلية 6000 دولار أمريكي للاعب "أ" (بشكلٍ لطيف مع "ب")، و0 دولار أمريكي للاعب "ب"، و3495 دولارًا أمريكيًا للاعب "ج" (مع ترك مبلغ صغير غير مُراهن، تحسبًا لرهان "أ" بكل شيء أو كل شيء باستثناء دولار واحد، ويكون مُخطئًا).
قبل أن يتحداني أحد حول كيفية رسم رقم عشوائي في المكان الفعلي، اسمحوا لي أن أقترح استراتيجية ستانفورد وونغ باستخدام عقرب الثواني في ساعتك لرسم رقم عشوائي من 1 إلى 60.
عُرض لأول مرة في المملكة المتحدة برنامج مسابقات جديد بعنوان " لون المال ". يُمنح متسابق واحد مبلغًا مستهدفًا عشوائيًا، يتراوح بين 55,000 و79,000 جنيه إسترليني. لكسب المال، يختار المتسابق 10 من 20 ماكينة بنكية، تحتوي كل منها على مبالغ تتراوح بين 1,000 و20,000 جنيه إسترليني، بزيادات متساوية قدرها 1,000 جنيه إسترليني. عندما يختار ماكينة، تبدأ بالعد تصاعديًا من 1,000 جنيه إسترليني، بزيادات متساوية قدرها 1,000 جنيه إسترليني.
يمكن للاعب أن يصرخ "توقف!" في أي وقت، وسيودع المبلغ الظاهر على الشاشة. إذا لم يتوقف اللاعب في الوقت المناسب، ونفد رصيد الآلة، فلن يودع شيئًا. تُقدم المضيفة إحصائيات، مثل عدد الآلات المتبقية للاختيار، والمبلغ المتبقي للربح، ومتوسط المبلغ المطلوب لكل آلة للفوز، والمبالغ المتبقية في الآلات.
يمكن للاعب "اللعب على الفجوات"، بمعنى أنه إذا تم اختيار سلسلة من الآلات، مثلاً 4 آلاف، 5 آلاف، و6 آلاف جنيه إسترليني، فمن المؤكد أن الآلة ستصل إلى 7000 جنيه إسترليني بمجرد تجاوزها حاجز 3000 جنيه إسترليني. سؤالي هو: ما نوع الاستراتيجية التي ينبغي للاعب اتباعها؟
هذا النوع من الأمور قد يستغرق أسابيع في تحليله. للأسف، قرأت رسالتك بعد ثلاثة أشهر تقريبًا من كتابتك، نظرًا لتراكم أسئلة "اسأل الساحر". يبدو أن صفحة ويكيبيديا تشير إلى أن هذا البرنامج كان فاشلًا، وتم إلغاؤه. ومع ذلك، لا يزال هذا يُمثل مشكلة مثيرة للاهتمام.
تُخبرك المضيفة بسهولة بمتوسط الكمية التي تحتاجها لكل آلة متبقية للوصول إلى لعبتك. بعد ساعات من التخطيط، لا أجد أفضل من تحديد هدف إيقاف أعلى بحوالي ٢٥٪ من المتوسط المطلوب. هذا مجرد تخمين، لذا من فضلك لا تطلب مني إثبات أنه الأمثل. كما ذكرت، استغل الفجوات أيضًا، ولا تتوقف أبدًا قبل كمية تم اختيارها بالفعل.
عندما يتبقى آلتان فقط، إذا كان المبلغ الإجمالي المطلوب ١٣٠٠٠ جنيه إسترليني أو أقل، فسأحاول الحصول عليه بالكامل من الآلة قبل الأخيرة. إذا كان ١٤٠٠٠ جنيه إسترليني أو أكثر، فسأحاول الحصول على نصفه من الآلة التالية.
إذا أُعيد هذا العرض، آمل أن يُخبرني قرائي في المملكة المتحدة. هذا هو نوع الألغاز التي قد تُثير اهتمامي، مثل لغز الأبدية ، الذي كان، صدفةً (أو لا صدفة)، أيضًا خارج المملكة المتحدة.
ملاحظة: لماذا تُكتب كلمة "colour" بـ au في المملكة المتحدة؟ هذا غير منطقي بالنسبة لي.
ما هو متوسط الجائزة لكل لكمة والاستراتيجية المثلى للعبة Punch a Bunch على The Price is Right؟
لمن لا يعرف قواعد اللعبة، تجدها مشروحة على موقع "برايس إز رايت" . تفضل بزيارة الموقع إذا لم تكن تعرف اللعبة، لأنني أفترض أنك تعرف القواعد. هناك أيضًا العديد من مقاطع فيديو اللعبة على يوتيوب. إليك مقطع فيديو قديم يُظهر فرصة ثانية، لكن الحد الأقصى للجائزة آنذاك كان 10,000 دولار فقط. أما الآن، فقد أصبح 25,000 دولار.
أولاً، لنحسب القيمة المتوقعة لجائزة غير مرتبطة بفرصة ثانية. يوضح الجدول التالي أن متوسط القيمة هو ١٣٧١.٧٤ دولارًا أمريكيًا.
توزيع جوائز "لكمة مجموعة" بدون فرصة ثانية
| جائزة | رقم | احتمال | الفوز المتوقع |
| 25000 | 1 | 0.021739 | 543.478261 |
| 10000 | 1 | 0.021739 | 217.391304 |
| 5000 | 3 | 0.065217 | 326.086957 |
| 1000 | 5 | 0.108696 | 108.695652 |
| 500 | 9 | 0.195652 | 97.826087 |
| 250 | 9 | 0.195652 | 48.913043 |
| 100 | 9 | 0.195652 | 19.565217 |
| 50 | 9 | 0.195652 | 9.782609 |
| المجموع | 46 | 1.000000 | 1371.739130 |
ثانيًا، احسب متوسط الجائزة التي تتضمن فرصة ثانية. يوضح الجدول التالي أن المتوسط هو ٢٢٥ دولارًا.
توزيع جوائز Punch a Bunch مع فرصة ثانية
| جائزة | رقم | احتمال | الفوز المتوقع |
| 500 | 1 | 0.250000 | 125.000000 |
| 250 | 1 | 0.250000 | 62.500000 |
| 100 | 1 | 0.250000 | 25.000000 |
| 50 | 1 | 0.250000 | 12.500000 |
| المجموع | 4 | 1.000000 | 225.000000 |
ثالثًا، أنشئ جدولًا للقيمة المتوقعة بناءً على عدد الفرص الثانية التي يحصل عليها اللاعب. يمكن حساب ذلك باستخدام عملية حسابية بسيطة. على سبيل المثال، احتمال وجود فرصتين ثانتين هو (4/50) × (3/49) × (46/48). الربح المتوقع مع وجود فرصتين ثانتين هو 1371.74 دولارًا أمريكيًا + s × 225 دولارًا أمريكيًا. يوضح الجدول التالي احتمالية ومتوسط الربح لعدد من الفرص الثانية يتراوح بين 0 و4.
طاولة إرجاع الجوائز
| فرص ثانية | احتمال | متوسط الفوز | الفوز المتوقع |
| 4 | 0.000004 | 2271.739130 | 0.009864 |
| 3 | 0.000200 | 2046.739130 | 0.408815 |
| 2 | 0.004694 | 1821.739130 | 8.551020 |
| 1 | 0.075102 | 1596.739130 | 119.918367 |
| 0 | 0.920000 | 1371.739130 | 1262.000000 |
| المجموع | 1.000000 | 1390.888067 |
وبالتالي فإن متوسط الفوز لكل لكمة (بما في ذلك الأموال الإضافية من الفرص الثانية) هو 1390.89 دولارًا.
يوضح الجدول التالي استراتيجيتي للحد الأدنى للفوز، بناءً على عدد اللكمات المتبقية. يُرجى العلم أنه يمكن للاعب الوصول إلى 1400 دولار أمريكي بجوائز 1000 دولار أمريكي + 250 دولارًا أمريكيًا، + 100 دولار أمريكي + 50 دولارًا أمريكيًا، من خلال ثلاث فرص ثانية.
استراتيجية الضربة القاضية
| اللكمات المتبقية | الحد الأدنى للوقوف |
| 3 | 5000 دولار |
| 2 | 5000 دولار |
| 1 | 1400 دولار |
تم طرح هذا السؤال ومناقشته في منتدى موقعي المرافق Wizard of Vegas .
ما هي الاستراتيجية المثلى لتقسيم أموالك في برنامج المسابقات Million Dollar Money Drop، إذا لم تكن متأكدًا من الإجابة؟
ولصالح القراء الآخرين، دعوني أراجع القواعد أولاً.
- يبدأ فريق اللاعبين بمبلغ 1,000,000 دولار.
- يتم إعطاء الفريق سؤال اختياري متعدد.
- على الفريق تقسيم أمواله على الإجابات المحتملة. أي مبلغ يُجمع على الإجابة الصحيحة ينتقل إلى السؤال التالي.
- يجب على الفريق استبعاد إجابة واحدة على الأقل تمامًا من خلال عدم وضع أي أموال عليها.
- تتكرر هذه العملية لعدة جولات. يُمنح اللاعب أيضًا فرصة واحدة لتغيير رأيه.
من البديهي أنه إذا كان الفريق متأكدًا من الإجابة، فعليه المراهنة بكل أمواله على الإجابة الصحيحة. إذا تمكن الفريق من تضييق نطاق الإجابة إلى اثنتين، مع منح كل منهما فرصة ٥٠٪ للصواب، فعليه تقسيم أمواله بالتساوي بين الخيارين.
يصبح الأمر أكثر صعوبة إذا مال الفريق نحو إجابة واحدة دون استبعاد إجابة واحدة أو أكثر من الإجابات الأخرى تمامًا. لنأخذ مثالًا. لنفترض أن الفريق حدد احتمال كل إجابة صحيحة كما يلي: أ ١٠٪، ب ٢٠٪، ج ٣٠٪، د ٤٠٪. كيف يُقسمون أمواله؟
أعتقد أن الحل يكمن في اتباع معيار كيلي . باختصار، يجب على الفريق تعظيم قيمة لوغاريتم ثروته مع كل سؤال. للقيام بذلك، عليك مراعاة مقدار ثروتك الحالية.
لنفترض أن ثروتك الحالية، التي جمعتها بشكل مستقل عن البرنامج، تبلغ 100,000 دولار. هذا هو سؤالك الأول، لذا لديك مليون دولار من أموال البرنامج لتقسيمها. استبعد أولًا الخيار الأقل احتمالًا، بما يتوافق مع قواعد البرنامج. ثم تريد تعظيم 0.2×log(100,000+b*1,000,000) + 0.3×log(100,000+c*1,000,000) + 0.4×log(100,000+d*1,000,000)، حيث تشير الأحرف الصغيرة a وb وc إلى الجزء المخصص لكل إجابة.
يمكن حل هذه المسألة باستخدام حساب التفاضل والتكامل وحل معادلة ثلاثية الحدود، أو التجربة والخطأ، أو -كما أُفضّل- خاصية "البحث عن الهدف" في برنامج إكسل. أيًا كان الحل الذي تستخدمه، فالإجابة الصحيحة هي وضع 18.9% على الخيار ب، و33.3% على الخيار ج، و47.8% على الخيار د.
بالطبع، لن يتمكن أيٌّ من المشاركين في البرنامج من إجراء كل هذه العمليات الحسابية في الوقت المسموح به، ناهيك عن حاجتك لنقل كميات كبيرة من النقود خلال ذلك الوقت. نصيحتي العملية هي تقسيم المبلغ بما يتناسب مع تقديرك لاحتمالية صحة الإجابة، بافتراض أن الخيار الأقل احتمالاً غير وارد. في هذا المثال، سيؤدي ذلك إلى تقسيم المبلغ بنسبة 22.2% على الخيار (ب)، و33.3% على الخيار (ج)، و44.4% على الخيار (د).
تم طرح هذا السؤال ومناقشته في منتدى موقعي المرافق Wizard of Vegas .
تحتوي يانصيب ميشيغان على لعبة ثلاثية اللاعبين وفقًا للقواعد التالية: هل هناك أي ميزة موقعية للتواجد في المركز الأخير في هذه اللعبة؟ ما هي الاستراتيجية الأمثل لكل لاعب؟ إليكم فيديوعلى يوتيوب يعرض اللعبة.
أولًا، لا توجد ميزة موقعية للتصرف الأخير. بما أن اللاعبين يُحفظون في حجرة عازلة للصوت أثناء لعب أي لاعب سابق، فلا يُهم الترتيب.
ثانيًا، يجب أن يكون هناك توازن ناش في اللعبة، حيث تكون استراتيجية البقاء برصيد x نقطة على الأقل أفضل من أي استراتيجية أخرى. السؤال هو إيجاد x.
ما فعلته هو أنني سألت نفسي: ما هي الاستراتيجية المتبعة إذا حصل كل لاعب، بدلاً من بطاقة مرقمة من ١ إلى ١٠٠، على رقم عشوائي موزع بالتساوي بين ٠ و١، وبحث عن النقطة س التي لا يكترث فيها أي منطقي مثالي بين التوقف والتبديل. بهذه الإجابة، يسهل تطبيقها على توزيع منفصل من ١ إلى ١٠٠.
سأتوقف عن الحديث هنا، وأترك لقرائي الاستمتاع بالمشكلة. للاطلاع على الإجابة والحل، يُرجى زيارة الروابط أدناه.
الإجابة على التوزيع المستمر من 0 إلى 1 .
الإجابة على التوزيع المنفصل من 1 إلى 100.
للحصول على حلي، الرجاء الضغط هنا (PDF) .
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
بافتراض عدم وجود معرفة بسعر أي شيء، ما هي الاستراتيجية المثلى للعبة السباق على السعر الصحيح؟
لمن لا يعرف القواعد، يُعطى اللاعب أربع بطاقات أسعار، وعليه وضعها على أربع قطع. عند الانتهاء، يسحب ذراعًا يُظهر عدد التطابقات الصحيحة. إذا كانت نقاط اللاعب أقل من أربع، فيمكنه إعادة ترتيب البطاقات والمحاولة مرة أخرى. يُسمح للاعب بالمحاولة لأكبر عدد ممكن خلال 45 ثانية.
نصيحتي هي تقديم اختيار ذي فرصة للفوز دائمًا، مع مراعاة تاريخ الاختيارات والنتائج السابقة. إذا كانت النتيجة الأولى صفرًا، فلا تعكس مجموعتين من علامتين، بل غيّر كل شيء موضعًا واحدًا في أي اتجاه.
إذا لم تتمكن من فهم المنطق فورًا، فسأشرحه لك أدناه. لاستخدام هذه الاستراتيجية، عيّن للوسوم المختلفة الأحرف A وB وC وD. ثم ضعها بالترتيب الموضح، من اليسار إلى اليمين على المسرح. ابدأ دائمًا بـ ABCD. ثم ابحث في سجل النوتات الموسيقية أدناه واختر تسلسل الوسوم المشار إليه لتسلسل النوتات الموسيقية.
إذا كان 0، ثم BCDA
إذا كانت 0-0، فإن CDAB
إذا كانت النتيجة 0-0-0، إذن DABC (يجب الفوز)
إذا كانت 0-1، ثم BDAC
إذا كانت النتيجة 0-1-0، إذن CADB (يجب الفوز)
إذا كانت 0-1-1، إذن CDBA
إذا كانت النتيجة 0-1-1-0، إذن DCAB (يجب الفوز)
إذا كانت 0-2، فإن BADC
إذا كانت النتيجة 0-2-0، فيجب الفوز بـ DCBA
إذا كان 1، ثم ACDB
إذا كانت النتيجة 1-0، فإن BDCA
إذا كان 1-0-0، إذن CABD
إذا كانت النتيجة 1-0-0-1، إذن CBAC (يجب الفوز)
إذا كان 1-1، ثم BDCA
إذا كان 1-1-0، إذن CABD
إذا كانت النتيجة 1-1-0-1، إذن CBAC (يجب الفوز)
إذا كانت النتيجة 1-1-1، إذن BCAD (يجب الفوز)
إذا كان 2، إذن ABDC
إذا كانت النتيجة 2-0، فيجب أن يكون BACD (يجب الفوز)
إذا كان 2-1، ثم ACBD
إذا كان 2-1-0، ثم DBCA
إذا كان 2-1-1، ثم ADCB
إذا كانت النتيجة 2-1-1-0، إذن CBAD (يجب الفوز)
يوضح الجدول التالي احتمال كل عدد من الدورات. تُظهر الخلية اليمنى السفلية العدد المتوقع للدورات وهو ١٠/٣.
لعبة السباق
| المنعطفات | التركيبات | احتمال | يعود |
|---|---|---|---|
| 1 | 1 | 0.041667 | 0.041667 |
| 2 | 4 | 0.166667 | 0.333333 |
| 3 | 8 | 0.333333 | 1.000000 |
| 4 | 8 | 0.333333 | 1.333333 |
| 5 | 3 | 0.125000 | 0.625000 |
| المجموع | 24 | 1.000000 | 3.333333 |
تمت مناقشة هذا السؤال في المنتدى الخاص بي في Wizard of Vegas .
ما هو احتمال فوز أي لاعب بمبلغ 25000 دولار في Showcase Showdown على Price is Right؟
للتوضيح للقراء الآخرين، دعوني أشرح ما تتحدثون عنه. لعبة "عرض المكافآت" تُلعب في برنامج "السعر مناسب". في هذه اللعبة، يقوم كل لاعب بتدوير عجلة، احتمالية توقفها متساوية عند كل قيمة قابلة للقسمة بالتساوي على 0.05 من 0.05 إلى 1.00. إذا لم تعجبه دورته الأولى، فيمكنه إعادة الدوران، مع إضافة الثانية إلى الأولى، ولكن إذا تجاوزت 1.00، فسيتم استبعاده فورًا. في حالة التعادل، يحصل كل لاعب على دورة واحدة في جولة كسر التعادل، ويفوز صاحب أعلى دورة. في حالة التعادل مرة أخرى، تتكرر هذه العملية حتى يتم كسر التعادل.
الهدف الرئيسي من مسابقة "مواجهة العرض" هو التأهل إلى "مواجهة العرض". كما تتوفر جوائز نقدية فورية، كما يلي:
- في الجولة الأولى، إذا حصل أي لاعب على إجمالي قدره 1.00 دولار، سواء في مبلغ واحد أو مجموع دورتين، فإنه يفوز بمبلغ 1000 دولار.
- في الجولة الأولى، والوحيدة، لكسر التعادل، إذا توقفت العجلة على 0.05 دولار أو 0.15 دولار، فإن اللاعب يفوز بمبلغ 10000 دولار.
- في الجولة الأولى، والوحيدة، لكسر التعادل، إذا توقفت العجلة على 1.00 دولار، فإن اللاعب يفوز بمبلغ 25000 دولار.
أشرح الاستراتيجية المثلى لمسابقة "عرض العروض" في العمود رقم ١٠١. بافتراض اتباع هذه الاستراتيجية، يُجيب الجدول التالي على أسئلتكم وأسئلة أخرى متنوعة.
إحصائيات عرض المواجهة
| سؤال | إجابة |
|---|---|
| الفائزون المتوقعون بالجولة الأولى بقيمة 1000 دولار | 0.253790 |
| احتمالية التعادل بين لاعبين | 0.113854 |
| احتمالية التعادل بين ثلاثة لاعبين | 0.004787 |
| الفائزون المتوقعون بالجولة الثانية بجائزة 10000 دولار | 0.024207 |
| الفائزون المتوقعون بالجولة الثانية بجائزة 25000 دولار | 0.012104 |
| إجمالي الجائزة المالية المتوقعة | 798.45 دولارًا |
| احتمال فوز أي لاعب بمبلغ 1000 دولار | 0.084597 |
| احتمال فوز أي لاعب بمبلغ 10000 دولار | 0.008069 |
| احتمال فوز أي لاعب بمبلغ 25000 دولار | 0.004035 |
يوضح الصف السفلي من الجدول أنه إذا قمت بإجراء Showcase Showdown، دون النظر إلى ترتيبك للدوران، فإن فرصك في الفوز بمبلغ 25000 دولار هي 0.004035، أو 1 في 248.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
في برنامج "الناجي"، كان هناك فريقان، أحدهما بتسعة لاعبين والآخر بستة. ثم وُزّعوا عشوائيًا في ثلاثة فرق جديدة، كل منها بخمسة لاعبين. تكوّن كل فريق جديد من ثلاثة أعضاء من الفريق السابق المكون من تسعة لاعبين، واثنين من الفريق السابق المكون من ستة لاعبين. ما احتمالات ذلك؟
لنسمِّ الفريق السابق المكون من تسعة لاعبين الفريق ١، والفريق المكون من ستة لاعبين الفريق ٢. عدد طرق اختيار ثلاثة لاعبين من الفريق ١ ولاعبين من الفريق ٢ هو combin(9,3)×combin(6,2) = ١٢٦٠. العدد الإجمالي لطرق اختيار خمسة لاعبين من أصل ١٥ هو combin(15,5) = ٣٠٠٣. لذا، فإن احتمال انقسام الفريق الأول بنسبة ٣/٢ لصالح الفريق ١ هو ١٢٦٠/٣٠٠٣ = ٤١.٩٦٪.
إذا حدث ذلك، فسيتبقى للفريق ١ ستة لاعبين وللفريق ٢ أربعة لاعبين. عدد طرق اختيار ثلاثة لاعبين من الفريق ١ ولاعبين من الفريق ٢ هو combin(6,3)×combin(4,2) = ١٢٠. العدد الإجمالي لطرق اختيار خمسة لاعبين من أصل ١٠ لاعبين متبقين هو combin(10,5) = ٢٥٢. لذا، فإن احتمال انقسام الفريق الثاني بنسبة ٣/٢ لصالح الفريق ١، بشرط انقسام الفريق الأول بنسبة ٣/٢ بالفعل، هو ١٢٠/٢٥٢ = ٤٧.٦٢٪.
إذا تم تقسيم الفريقين الجديدين الأولين بنسبة 3/2، لصالح الفريق السابق 1، فسيتم تقسيم الفريق النهائي بنسبة 3/2 بين المتبقيين.
وبالتالي فإن إجابة سؤالك هي 41.96% × 47.62% × 100% = 19.98%.
الصيغ:
الجمع(x،y)=x!/((y!*(xy)!)
x! = 1*2*3*...*x
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
أعتقد أن جيمس هولزهاور خسر عمدًا أمام إيما في مباراته الأخيرة. دليلي أنه كان يراهن بمبالغ كبيرة في كل مباراة حتى تلك اللحظة، وفجأة راهن بمبالغ منخفضة ضد إيما. أظن أن المنتجين يريدون كين جينينغز لتقديم البرنامج بعد استقالة أليكس. كان البرنامج ليكون أكثر إثارة لو كان لدى المذيع سجلات في كلا البرنامجين وأموال ربحها. وهكذا، دفعوا لجيمس ليخسر المباراة.
دعوني أُهيئ المشهد. في 3 يونيو 2019، كان جيمس على وشك تحطيم الرقم القياسي لإجمالي الأموال التي ربحها في المباريات العادية، والذي لا يزال قائمًا عند 2,520,700 دولار أمريكي. كان متوسط فوز جيمس في المباراة الواحدة أعلى بكثير مما كان يحتاجه لتحطيم الرقم القياسي. لذا، كانت جميع الأنظار تترقب في 3 يونيو لتحطيم الرقم القياسي.
بدلاً من ذلك، ما حدث ليس فقط أن جيمس لم يحطم الرقم القياسي، بل خسر. أما الفائزة، إيما، فقد لعبت لعبة استراتيجية قوية جدًا، بالإضافة إلى إتقانها استخدام الجرس وإجابتها الصحيحة. لعبت كعادتها. قبل دخولها إلى لعبة "الخطر النهائي"، كانت النتائج:
- إيما - 26,600 دولار
- جيمس - 23400 دولار
- جاي — 11000 دولار
في هذه الحالات، حيث يمتلك صاحب المركز الثاني أكثر من نصف رصيد المركز الأول، بينما لا يمتلك صاحب المركز الثالث ذلك، عادةً ما يعتمد الأمر على اختيار صاحب المركز الأول والثاني رهانهما النهائي. رهان مرتفع على المركز الأول يكفي لضمان الفوز إذا كان صحيحًا. بمعنى آخر، ضعف رصيد المركز الثاني مطروحًا منه رصيد المركز الأول بالإضافة إلى دولار واحد. هذا ما فعلته إيما تمامًا برهانها 2 × 23,400 دولار - 26,600 دولار + دولار واحد = 20,201 دولار. في أغلب الأحيان، يفعل صاحب المركز الأول هذا.
مع ذلك، لم يكن جيمس يعلم ما ستفعله إيما عند تحديد رهانه. يوضح الجدول التالي من سيفوز بناءً على تركيبة الرهانات.
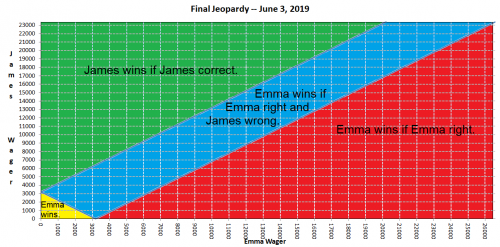
انقر على الصورة للحصول على نسخة أكبر.
إذا راهنت إيما بمبلغ 20201 دولارًا على الأقل، فإنها ستضمن الفوز إذا كانت صحيحة.
إذا راهنت إيما بمبلغ منخفض فإنها ستفوز إذا (أ) راهن جيمس بمبلغ منخفض أو (ب) راهن جيمس بمبلغ مرتفع وكان مخطئًا.
إذا راهن جيمس بمبالغ عالية فإنه يفوز إذا (أ) راهنت إيما بمبالغ عالية، وكانت إيما مخطئة، وكان جيمس على حق، أو (ب) راهنت إيما بمبالغ منخفضة وكان جيمس على حق.
إذا راهن جيمس بمبلغ منخفض فإنه يفوز، وإذا راهنت إيما بمبلغ مرتفع وكانت مخطئة.
لو كان هناك منطقيون بارعون يلعبون، لكان كلاهما قد عدّل قراراتهما عشوائيًا. مع ذلك، نادرًا ما يتراجع القائد في هذه المواقف التي يُمكن فيها القبض عليه. إذا توقع جيمس أن تتراجع إيما، فعليه ذلك بالتأكيد. بهذه الطريقة، لن يضطر للفوز في لعبة "الخطر النهائي"، بل عليه فقط أن يأمل في أن تفشل إيما.
كان عرض جيمس الفعلي هو المبلغ الصحيح لتغطية جاي إذا راهن جاي بكل شيء وكان على حق: 23400 دولار - 2 × 11000 دولار - 1 دولار = 1399 دولارًا، وهو ما كان رهانًا منخفضًا لأغراض الفوز على إيما.
إذا كان هذا صحيحا، فإن جيمس سوف يحصل على 1000 دولار إضافية لحصوله على المركز الثاني، مقارنة بالمركز الثالث.
في الختام، أرفض تمامًا نظرية المؤامرة القائلة بأن جيمس هو من أضاع المباراة. لقد لعب بالطريقة الصحيحة وخسر بسبب مواجهة منافس قوي وما يُطلق عليه معظم الناس "سوء حظ".
الروابط الخارجية
- قاعة مشاهير لعبة Jeopardy
- جيمس هولزهاور يتحدث عن لعبة Jeopardy — مناقشة في المنتدى الخاص بي في Wizard of Vegas.
في لعبة "فاينل جيباردي"، ما هي الاستراتيجية الأمثل إذا كان رصيد اللاعب الثاني أكثر من ثلثي رصيد اللاعب الأول؟ بافتراض أن اللاعب الثالث ليس عاملاً مؤثراً.
دعوني أوضح لكم أولاً: التحليل التالي مبني على متوسطات إحصائية. على اللاعب الحقيقي أن يُجري تعديلات ذهنية على مدى معرفته بفئة الخطر النهائي، بالإضافة إلى تقدير فرص خصمه في الإجابة الصحيحة.
للإجابة على سؤالك، نظرت أولاً إلى أربعة مواسم من البيانات من أرشيف لعبة Jeopardy لمعرفة التركيبات الأربعة المحتملة للاعب الأول (المتصدر) واللاعب الثاني (المطارد) الذين حصلوا على النتيجة الصحيحة أو الخاطئة في لعبة Jeopardy النهائية.
بطاقة النتائج النهائية للعبة Jeopardy
| اللاعب الرائد | مطاردة اللاعب الصحيح | مطاردة اللاعب غير صحيحة | المجموع |
|---|---|---|---|
| صحيح | 29.0% | 25.5% | 54.5% |
| غير صحيح | 17.7% | 27.8% | 45.5% |
| المجموع | 46.8% | 53.2% | 100.0% |
قبل المضي قدمًا، دعونا نحدد بعض المتغيرات:
x = احتمال أن يصبح اللاعب الرائد عالياً.
y = احتمالية ارتفاع اللاعب المطارد.
f(x,y) = احتمال فوز اللاعب الأعلى.
دعونا نعبر عن f(x,y) من حيث x و y من الجدول أعلاه:
f(x,y) = 0.823xy + 0.545x(1-y) + 0.468(1-x)y + (1-x)(1-y)
f(x,y) = 0.810 xy - 0.455x - 0.532y + 1
للعثور على القيم المثالية لـ x و y، دعنا نأخذ المشتق لـ f(x,y) بالنسبة إلى كل من x و y.
f(x,y) d/dx = -0.455 + 0.810y = 0
وبالتالي y = 0.455/0.810 = 0.562
f(x,y) d/dy = -0.532 + 0.810x = 0
وبالتالي x = 0.523/0.810 = 0.657
لذا، يجب على اللاعب صاحب الرهان المرتفع أن يراهن باحتمالية عالية تبلغ 65.7%، ويجب على اللاعب صاحب الرهان المنخفض أن يراهن باحتمالية عالية تبلغ 56.2%.
بناءً على المشاهدة، أعتقد أن اللاعبين الكبار يراهنون بمبالغ عالية تزيد عن 65.7% من الوقت، وبالتالي إذا كنت في المركز الثاني، فسأراهن بمبالغ منخفضة.
إذا اتبع كلا اللاعبين استراتيجية التوزيع العشوائي هذه، فإن احتمال فوز اللاعب المتقدم هو 70.1%.
بصرف النظر عن النظريات، إذا كنتَ متصدرًا، فتوقع ما سيفعله اللاعب المُطارد وافعل المثل. أما إذا كنتَ مُطاردًا، فتوقع ما سيفعله اللاعب المُتصدر وافعل عكسه. تُطبّق هذه الاستراتيجية في جميع البطولات المماثلة.تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
في بداية جولة "جيبردي"، لماذا يبدأ بعض اللاعبين، مثل جيمس هولتزهاور، بالاختيار من أسفل القائمة؟ ألا يكون من الأفضل البدء بالأسئلة الأسهل في الأعلى، جزئيًا لضمان فهمٍ صحيحٍ للفئة، والتي قد تكون صعبةً أحيانًا؟
السبب هو أن الأرقام المزدوجة اليومية تُوضع في الصفوف الثلاثة السفلية بنسبة 91.5%. يوضح الجدول التالي مواقعها على اللوحة، حيث تم العثور على أكثر من 13,660 رقمًا مزدوجًا يوميًا.
موقع مزدوج يوميًا
| صف | العمود 1 | العمود 2 | العمود 3 | العمود 4 | العمود 5 | العمود 6 | |
|---|---|---|---|---|---|---|---|
| 1 | 5 | - | 3 | 3 | 2 | 3 | 16 |
| 2 | 280 | 137 | 216 | 167 | 207 | 140 | 1,147 |
| 3 | 820 | 442 | 677 | 658 | 643 | 472 | 3,712 |
| 4 | 1,095 | 659 | 982 | 907 | 895 | 627 | 5,165 |
| 5 | 787 | 403 | 670 | 671 | 613 | 476 | 3,620 |
| المجموع | 2,987 | 1,641 | 2,548 | 2,406 | 2,360 | 1,718 | 13,660 |
المصدر: أرشيف ج!
وهنا نفس البيانات في شكل عدد المرات التي تم فيها العثور على Daily Double في كل خلية من اللوحة.
احتمالية مضاعفة يومية
| صف | العمود 1 | العمود 2 | العمود 3 | العمود 4 | العمود 5 | العمود 6 | |
|---|---|---|---|---|---|---|---|
| 1 | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.1% |
| 2 | 2.0% | 1.0% | 1.6% | 1.2% | 1.5% | 1.0% | 8.4% |
| 3 | 6.0% | 3.2% | 5.0% | 4.8% | 4.7% | 3.5% | 27.2% |
| 4 | 8.0% | 4.8% | 7.2% | 6.6% | 6.6% | 4.6% | 37.8% |
| 5 | 5.8% | 3.0% | 4.9% | 4.9% | 4.5% | 3.5% | 26.5% |
| المجموع | 21.9% | 12.0% | 18.7% | 17.6% | 17.3% | 12.6% | 100.0% |
سبب البحث عن "المضاعفات اليومية" هو أنها طريقة جيدة لمضاعفة نقاطك. لدى معظم المتسابقين احتمالية تتراوح بين 80% و90% في الحصول على أي إجابة صحيحة. من المهم جدًا الحصول على مبلغ متساوٍ على رهان تكون احتمالية فوزك فيه 80% أو 90%. من أهم أسباب فوز جيمس هولتزهاور بهذا القدر هو بحثه المكثف عن "المضاعفات اليومية"، ثم المراهنة بكل شيء في معظم الأحيان عند العثور عليها. وهذا ما أدى أيضًا إلى خسارته أمام إيما، عندما استخدمت نفس الاستراتيجية ضده.
ما هي أفضل استراتيجية للعب لعبة Race على السعر الصحيح، على افتراض أن اللاعب ليس لديه فكرة عن أسعار الجوائز؟
ولمصلحة القراء الذين ليسوا على دراية باللعبة، إليكم مقطع فيديو لها.
أعتقد أن الاستراتيجية التالية تُنتج متوسطًا أدنى لعدد الأدوار. هناك العديد من الاستراتيجيات التي تُعادلها، لكنني لا أعتقد أن أيًا منها يُمكن أن يُنافسها.
لاستخدام الاستراتيجية، قم بتسمية علامات الأسعار الأربعة بالأرقام 1 و2 و3 و4. ضعها على الجوائز الأربع وفقًا لسجل عدد الجوائز التي حصلت عليها بشكل صحيح في الماضي، بدءًا من الدور الأول على اليسار.
استراتيجية لعبة السباق
| تاريخ | الجائزة 1 | الجائزة 2 | الجائزة 3 | الجائزة 4 |
|---|---|---|---|---|
| لا أحد | 1 | 2 | 3 | 4 |
| 0 | 2 | 1 | 4 | 3 |
| 0,0 | 3 | 4 | 2 | 1 |
| 0,0,0 | 4 | 3 | 1 | 2 |
| 0,0,2 | 3 | 4 | 1 | 2 |
| 0,0,2,0 | 4 | 3 | 2 | 1 |
| 0,2 | 2 | 3 | 4 | 1 |
| 0,2,0 | 4 | 1 | 2 | 3 |
| 0,2,1 | 2 | 4 | 1 | 3 |
| 0,2,1,0 | 3 | 1 | 4 | 2 |
| 1 | 1 | 3 | 4 | 2 |
| 1,0 | 2 | 4 | 3 | 1 |
| 1,0,0 | 3 | 1 | 2 | 4 |
| 1,0,0,0 | 4 | 2 | 1 | 3 |
| 1,1 | 1 | 4 | 2 | 3 |
| 1,1,0 | 2 | 3 | 1 | 4 |
| 1,1,0,0 | 3 | 2 | 4 | 1 |
| 1,1,0,0,0 | 4 | 1 | 3 | 2 |
| 2 | 2 | 1 | 3 | 4 |
| 2,0 | 1 | 2 | 4 | 3 |
| 2,1 | 1 | 3 | 2 | 4 |
| 2,1,0 | 4 | 2 | 3 | 1 |
| 2،1،1 | 1 | 4 | 3 | 2 |
| 2,1,1,0 | 3 | 2 | 1 | 4 |
يوضح الجدول التالي احتمالية استغراق ترتيب بطاقات الأسعار الأربعة من 1 إلى 5 دورات من أصل 24 طريقة ممكنة.
عدد الأدوار المطلوبة
| المنعطفات | رقم | احتمال |
|---|---|---|
| 1 | 1 | 4.17% |
| 2 | 4 | 16.67% |
| 3 | 8 | 33.33% |
| 4 | 9 | 37.50% |
| 5 | 2 | 8.33% |
| المجموع | 24 | 100.00% |
إذا أخذنا حاصل الضرب النقطي، فإن متوسط عدد الدورات المطلوبة، بموجب هذه الاستراتيجية، هو 3.29167.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
سمعتُ شيئًا عن قاعدة الثلثين في الرهان على لعبة Final Jeopardy. هل تعرفها؟
نعم. يُشير إلى تغيير في استراتيجية اللاعب الثاني إذا كانت نتيجة اللاعب الأول أعلى من ثلثي النتيجة.
دعونا نبسط الوضع إلى لعبة لاعبين، على النحو التالي:
- الحالة أ: المركز الثاني يحتوي على أقل من نصف المركز الأول.
- الموقف ب: اللاعب الثاني لديه ما بين 1/2 و 2/3 من المركز الأول.
- الحالة ج: المركز الثاني حصل على أكثر من ثلثي المركز الأول.
قبل أن أواصل، دعوني أذكّر القارئ بتغيير في قواعد لعبة "جيوباردي" يتعلق بالتعادل بعد المرحلة النهائية. لم يعد كلا اللاعبين يتقدمان، ولكن أصبح هناك الآن سؤال لكسر التعادل بالموت المفاجئ. هذا هو الوضع .
الوضع أ
ليكن A = 10000 دولار و B = 4000 دولار
لا ينبغي للاعب "أ" المخاطرة بالخسارة بمراهنة لا تزيد عن "أ-2ب-1". إذا لم يكن واثقًا من هذه الفئة، فيمكنه المراهنة بـ 0 دولار. في كلتا الحالتين، يضمن الفوز. في هذه الحالة، يجب على "أ" المراهنة بمبلغ يتراوح بين 0 و1999 دولارًا.
لا أمل للاعب "ب" إلا إذا راهن "أ" كثيرًا وأخفق. هنا، على "ب" أن يأخذ في الاعتبار نتيجة المركز الثالث ويحاول البقاء متفوقًا عليه، إن استطاع، ويفوز بـ ٢٠٠٠ دولار للمركز الثاني، بدلًا من ١٠٠٠ دولار للمركز الثالث.
الوضع ب
ليكن A = 10000 دولار و B = 6000 دولار
استراتيجية اللاعب (أ) هي توقع أن يراهن (ب) بكل شيء، وأن يراهن بما يكفي لتغطية 2B إذا كانت الإجابة صحيحة. مع ذلك، وللتأكد من سلامته، يجب ألا يراهن كثيرًا حتى لا ينخفض عن (ب) إذا كانت الإجابة خاطئة. في هذه الحالة، يجب أن يراهن على الأقل على 2B-A+1 وAB-1. في هذه الحالة، يتراوح النطاق بين 2001 دولار و3999 دولار.
استراتيجية "ب" هي الحصول على ما يكفي لاجتياز "أ" إذا كان صحيحًا، ورفع نتيجته الإجمالية. في هذه الحالة، 4001 دولار و6000 دولار.
إذا نفّذ كلا اللاعبين ما هو متوقع منهما واتبعا هذه الاستراتيجية، فلن يفوز اللاعب ب إلا إذا كان أ مخطئًا و ب مُصيبًا. احتمال ذلك حوالي ١٩٪.
الوضع ج
هنا تصبح الأمور أكثر تعقيدًا وتتضمن المزيد من نظرية الألعاب والعشوائية.
ليكن A=10,000 دولار و B=7,000 دولار.
قبل الخوض في التفاصيل، من المهم تقدير احتمالية الإجابة الصحيحة على لغز "الخطر النهائي". بناءً على المواسم من 30 إلى 34، كانت إجابة اللاعب صاحب المركز الأول صحيحة بنسبة 52%، بينما كانت إجابة اللاعب صاحب المركز الثاني صحيحة بنسبة 46%. مع ذلك، ترتبط هذه الاحتمالات ارتباطًا إيجابيًا. فيما يلي تفصيل لجميع الاحتمالات الأربعة:
- كلاهما صحيح: 27%
- المركز الأول صحيح، المركز الثاني غير صحيح: 25%
- المركز الأول غير صحيح، المركز الثاني صحيح: 19%
- كلاهما غير صحيح بنسبة 29%.
على الرغم من أن متوسط لعبة Jeopardy يبلغ 49% للاعبين الأولين، فإن احتمال أن يكون كلاهما على حق أو كلاهما على خطأ هو 56%.
بالطبع، يمكن أن تتغير هذه الاحتمالات بناءً على الفئة، ولكن دعونا نبقي الأمور بسيطة ونستخدم الاحتمالات المذكورة أعلاه.
في هذه الحالة، لا يضطر اللاعب ب إلى الاعتماد على خطأ أ وصواب ب. يمكنه المراهنة بمبلغ منخفض، مثلاً 0 دولار، مما يضمن الفوز إذا أخطأ أ. بمعنى آخر، إذا راهن أ بما يكفي لتغطية رهان ب، إذا كان مصيباً، فإنه يُخاطر بالخسارة تحت رهان ب إذا أخطأ وراهن ب 0 دولار.
مع ذلك، إذا تنبأ أ بأن ب سيراهن بمبلغ منخفض، لنقل 0 دولار، فيمكن لـ أ ضمان الفوز بمراهنته أيضًا بمبلغ 0 دولار. لكلا اللاعبين خياران: إما أن يكونا منخفضين أو مرتفعين. يجب أن يرغب أ في المراهنة بنفس طريقة ب، ويجب أن يرغب ب في المراهنة بعكس طريقة ب. لو كان كلا اللاعبين منطقيين بارعين، لكانا قد اتخذا قراراتهما عشوائيًا.
في هذه الحالة، يجب أن يكون أعلى رهان من قِبل A هو 2B-A+1 إلى AB-1، كما هو الحال في الحالة B. في هذه الحالة، يكون الرهان 2,999 دولارًا و4,001 دولارًا. أما الرهان المنخفض من قِبل A، فيكون 0 دولارًا.
يجب أن يكون الرهان المرتفع من قِبل (ب) مماثلاً للرهان في الحالة (ب)، مع رهانات كافية لتجاوز (أ) إذا كانت صحيحة. في هذه الحالة، 3001 دولار و7000 دولار. يجب أن يكون الرهان المنخفض من قِبل (ب) 0 دولار.
سامحني إذا تخطيت الرياضيات وانتقلت مباشرة إلى استراتيجيات التوزيع العشوائي لكلا اللاعبين.
يجب على اللاعب (أ) أن يختار الرهان العالي باحتمالية 62.3% والرهان المنخفض باحتمالية 37.7%.
يجب أن يكون اللاعب B مرتفعًا باحتمالية 61.2% ومنخفضًا باحتمالية 38.8%.
بافتراض أن كلا اللاعبين اتبعا استراتيجية التوزيع العشوائي هذه واحتمالات كون الاختيار صحيحًا المذكورة أعلاه، فإن احتمال فوز اللاعب (أ) هو 65.2%.
إذا كان لدى اللاعب أ أكثر من 2/3 من نقاط اللاعب ب، فإن احتمال فوزه سيرتفع إلى 81.0%.
يجب على كلا اللاعبين أن يأخذوا في الاعتبار أهمية قاعدة 2/3 عند المراهنة على Double Jeopardy.